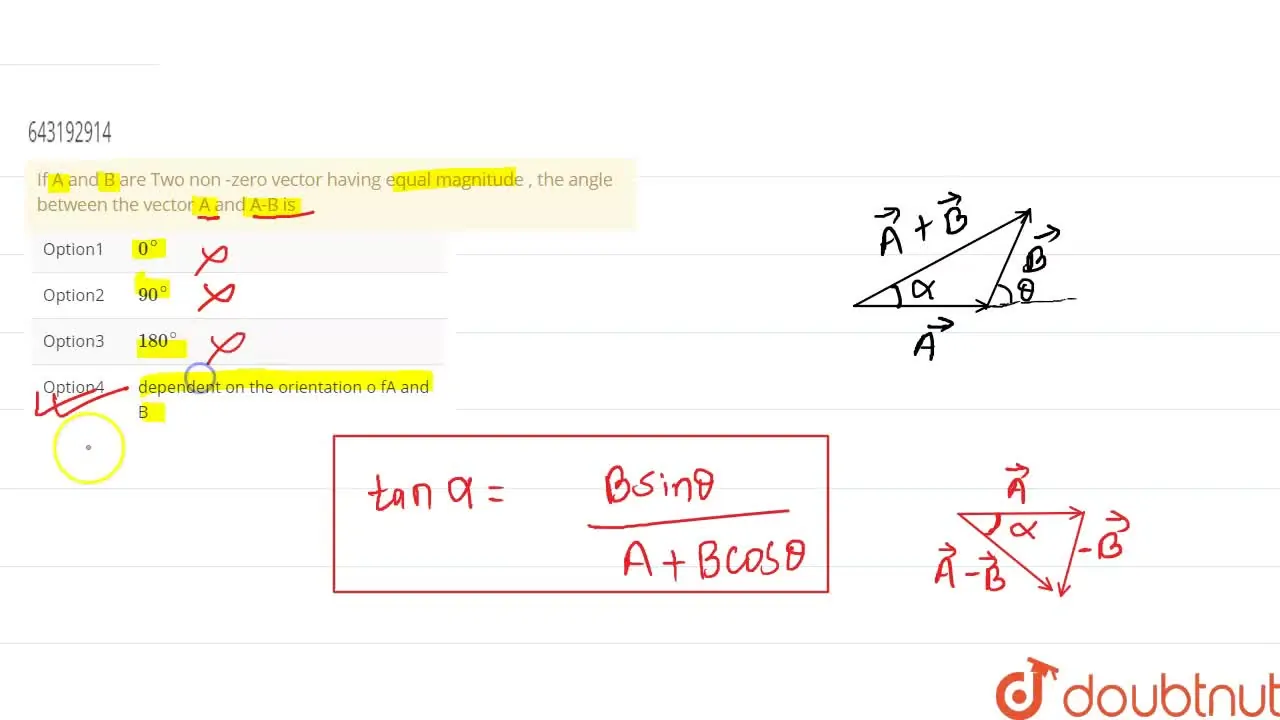
If A and B are Two non -zero vector having equal magnitude , the angle between the vector A and A-B is
0∘
90∘
180∘
dependent on the orientation o fA and B
The correct Answer is:D
(d) Suppose angle between two vector A and B of equal magniitude is θ then angle between Aand A-B will be 180∘−θ2or90∘−θ2 Here this angle will depend on the abgle between AandB Or θ

Related Playlists
Similar Questions
Given that →A+→B+→C=→0. Out of three vectors, two are equal in magnitude and the magnitude of the third vectors is √2 times that of either of the two having equal magnitude. Find the angles between the vectors.
View SolutionGiven that →A+→B+→C=→0. Out of three vectors,two are equal in magnitude and the magnitude of the third vectors is √2 times that of either of the two having equal magnitude. Find the angles between the vectors.
View SolutionGiven that →A+→B+→C=0, out of three vectors two are equal in magnitude and the magnitude of third vector is √2 times that of either of two having equal magnitude. Then angle between vectors are given by
View SolutionResultant of two vector of equal magnitude A is
View Solutionif →a,→band→c are mutally perpendicular vectors of equal magnitudes, then find the angle between vectors and →a+→b+→c.
View SolutionIf →a,→b,and→c are mutually perpendicular vectors of equal magnitudes, then find the angle between vectors →aand→a+→b+→c.
View SolutionTwo vector A and B have equal magnitudes. Then the vector A+B is perpendicular to
View SolutionIf A and B are two vectors such that |A+B|=2|A-B|. The angle between vectors A and B is
View SolutionIf a,b and c are three non-zero vectors such that no two of these are collinear. If the vector a+2b is collinear with c and b+3c is collinear with a(λ being some non-zero scalar), then a+2b+6c is equal to
View Solution→Aand→B are two vectors having the same magnitude . What is the condition that (i) the vector sum →A+→B and (ii) the vector differece →A+→B have the same magnitude as →Aand→B ?
View Solution