Resultant of two vetors A and B is given by |R|={|A|−|B|}.angle between A and B will be
90∘
180∘
0∘
none of these
The correct Answer is:B
To find the angle between two vectors →A and →B given that the resultant vector →R is defined by the equation |→R|=|→A|−|→B|, we can follow these steps:
Step 1: Understand the Resultant Vector
The resultant vector →R can be expressed using the formula:
|→R|=√|→A|2+|→B|2+2|→A||→B|cosθ
where θ is the angle between vectors →A and →B.
Step 2: Set Up the Equation
According to the problem, we know:
|→R|=|→A|−|→B|
We can square both sides to eliminate the square root:
(|→A|−|→B|)2=|→A|2+|→B|2+2|→A||→B|cosθ
Step 3: Expand the Left Side
Expanding the left side gives:
|→A|2−2|→A||→B|+|→B|2=|→A|2+|→B|2+2|→A||→B|cosθ
Step 4: Simplify the Equation
Now, we can cancel |→A|2 and |→B|2 from both sides:
−2|→A||→B|=2|→A||→B|cosθ
Step 5: Solve for cosθ
Dividing both sides by 2|→A||→B| (assuming |→A| and |→B| are not zero):
−1=cosθ
Step 6: Find the Angle
The angle θ that satisfies cosθ=−1 is:
θ=180∘
Conclusion
Thus, the angle between vectors →A and →B is 180∘.
Final Answer
The angle between →A and →B is 180∘.
---
The resultant vector →R can be expressed using the formula:
|→R|=√|→A|2+|→B|2+2|→A||→B|cosθ
where θ is the angle between vectors →A and →B.
According to the problem, we know:
|→R|=|→A|−|→B|
We can square both sides to eliminate the square root:
(|→A|−|→B|)2=|→A|2+|→B|2+2|→A||→B|cosθ
Expanding the left side gives:
|→A|2−2|→A||→B|+|→B|2=|→A|2+|→B|2+2|→A||→B|cosθ
Now, we can cancel |→A|2 and |→B|2 from both sides:
−2|→A||→B|=2|→A||→B|cosθ
Dividing both sides by 2|→A||→B| (assuming |→A| and |→B| are not zero):
−1=cosθ
The angle θ that satisfies cosθ=−1 is:
θ=180∘
Thus, the angle between vectors →A and →B is 180∘.
The angle between →A and →B is 180∘.
Topper's Solved these Questions
Similar Questions
The ratio of maximum and minimum magnitude of the resultant of two vectors →A and →B is 3:2. The relation between A and B is
View SolutionIf A.B=A×B, then angle between A and B is
View SolutionFind R≠t between A and B.
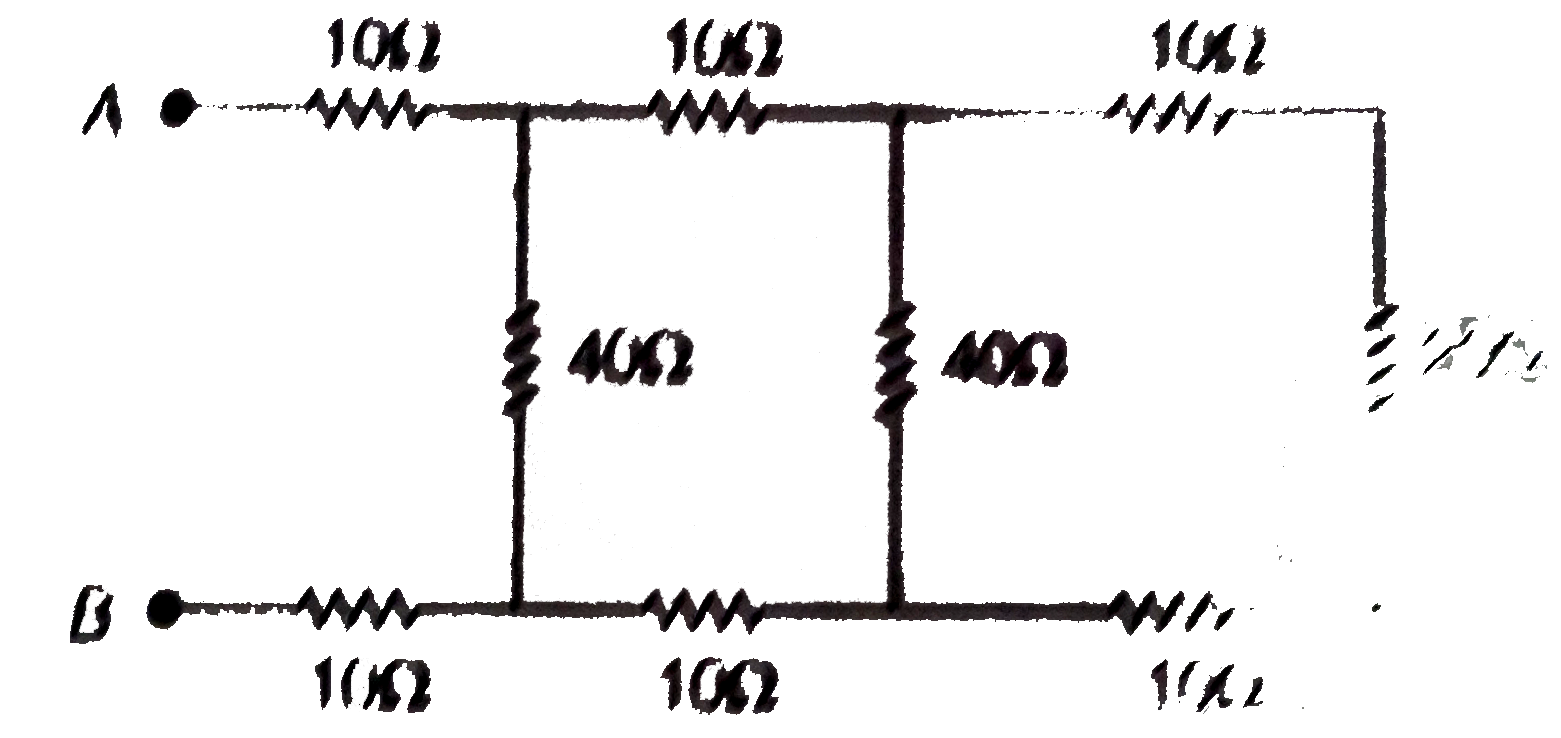
View SolutionThe resultant of two vector A and B is at right angles to A and its magnitude is half of B. Find the angle between A and B.
View SolutionThe resultant of two vectors A and B is perpendicular to the vector A and its magnitude is equal to half the magnitude of vector B. The angle between A and B is -

View SolutionFind the magnitude and direction of the resultant of two vectors A and B in the terms of their magnitudes and angle θ between them.

View SolutionIf A and B are two vectors such that |A+B|=2|A-B|. The angle between vectors A and B is
View SolutionThe resultant of two vectors →A and →B is perpendicular to the vector →A and its magnitudes is equal to half of the magnitudes of vector →B (figure). The angle between →A and →B is

View SolutionAssertion If angle between a and b is 30∘ . Then angle between 2a and −b2 will be 150∘
Reason Sign of dot product of two vectors tells you whether angle between two vectors is acute or obtuse .
View SolutionIf |a+b|>|a−b|, then the angle between a and b is
View Solution
