The thermal conductivity of a rod depends on
length
mass
area of x-section
material of the rod
The correct Answer is:D
To determine the factors on which the thermal conductivity of a rod depends, we can analyze the concept of thermal conductivity and its relationship with the properties of materials.
1. Understanding Thermal Conductivity:
Thermal conductivity (K) is a material property that indicates how well a material can conduct heat. It is defined as the amount of heat (dq) that passes through a unit area (A) of the material in a unit time (dt) when there is a temperature gradient (ΔT) across a distance (dx).
2. Formula for Heat Transfer:
The heat transfer through conduction can be expressed using Fourier's law:
dqdt=−K⋅A⋅ΔTdx
Here, K is the thermal conductivity, A is the cross-sectional area, ΔT is the temperature difference, and dx is the length of the rod.
3. Factors Affecting Thermal Conductivity:
- Material of the Rod: The thermal conductivity is primarily dependent on the type of material. Different materials have different intrinsic properties that affect how easily heat can flow through them. For example, metals like copper have high thermal conductivity due to the presence of free electrons.
- Cross-sectional Area (A): While the thermal conductivity itself is a property of the material, the rate of heat transfer does depend on the area through which heat is conducted. A larger area allows more heat to flow.
- Length of the Rod (dx): The length of the rod does not affect the thermal conductivity itself but affects the temperature gradient. A longer rod will have a greater temperature drop for the same amount of heat transferred.
- Mass: The mass of the rod does not directly affect thermal conductivity; however, it can influence the heat capacity of the rod, which is a different property.
4. Conclusion:
The thermal conductivity of a rod primarily depends on the material of the rod. Other factors like length and cross-sectional area influence the heat transfer rate but do not change the thermal conductivity value for a given material.
Final Answer:
The thermal conductivity of a rod depends on the material of the rod.
Thermal conductivity (K) is a material property that indicates how well a material can conduct heat. It is defined as the amount of heat (dq) that passes through a unit area (A) of the material in a unit time (dt) when there is a temperature gradient (ΔT) across a distance (dx).
The heat transfer through conduction can be expressed using Fourier's law:
dqdt=−K⋅A⋅ΔTdx
Here, K is the thermal conductivity, A is the cross-sectional area, ΔT is the temperature difference, and dx is the length of the rod.
- Material of the Rod: The thermal conductivity is primarily dependent on the type of material. Different materials have different intrinsic properties that affect how easily heat can flow through them. For example, metals like copper have high thermal conductivity due to the presence of free electrons.
- Cross-sectional Area (A): While the thermal conductivity itself is a property of the material, the rate of heat transfer does depend on the area through which heat is conducted. A larger area allows more heat to flow.
- Length of the Rod (dx): The length of the rod does not affect the thermal conductivity itself but affects the temperature gradient. A longer rod will have a greater temperature drop for the same amount of heat transferred.
- Mass: The mass of the rod does not directly affect thermal conductivity; however, it can influence the heat capacity of the rod, which is a different property.
The thermal conductivity of a rod primarily depends on the material of the rod. Other factors like length and cross-sectional area influence the heat transfer rate but do not change the thermal conductivity value for a given material.
The thermal conductivity of a rod depends on the material of the rod.
Topper's Solved these Questions
- CALORIMETRY AND HEAT TRANSFERBOOK - DC PANDEY ENGLISHCHAPTER - CALORIMETRY AND HEAT TRANSFEREXERCISE - Check points 16.4
29 Videos
- CALORIMETRY AND HEAT TRANSFERBOOK - DC PANDEY ENGLISHCHAPTER - CALORIMETRY AND HEAT TRANSFEREXERCISE - Taking it together
51 Videos
- CALORIMETRY AND HEAT TRANSFERBOOK - DC PANDEY ENGLISHCHAPTER - CALORIMETRY AND HEAT TRANSFEREXERCISE - Check point 16.2
10 Videos
- CALORIMETRY & HEAT TRANSFERBOOK - DC PANDEY ENGLISHCHAPTER - CALORIMETRY & HEAT TRANSFEREXERCISE - Level 2 Subjective
14 Videos
- CENTRE OF MASSBOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - Medical entrances gallery
27 Videos
Similar Questions
A: The thermal conductivity of a body depends on its material and dimensions.
R: Thermal conductivity is proportional to length and inversely proportional to area cross-section of body.
View SolutionA metallic rod of cross-sectional area 20 cm2, with the lateral surface insulated to prevent heat loss, has one end immersed in boiling water and the other in ice water mixture. The heat conducted through the rod melts the ice at the rate of 1 gm for every 84 sec. The thermal conductivity of the rod is 160Wm−1K−1. Latent heat of ice=80 cal/gm, 1 ca=4.2 joule. What is the length (in m) of the rod?
View Solution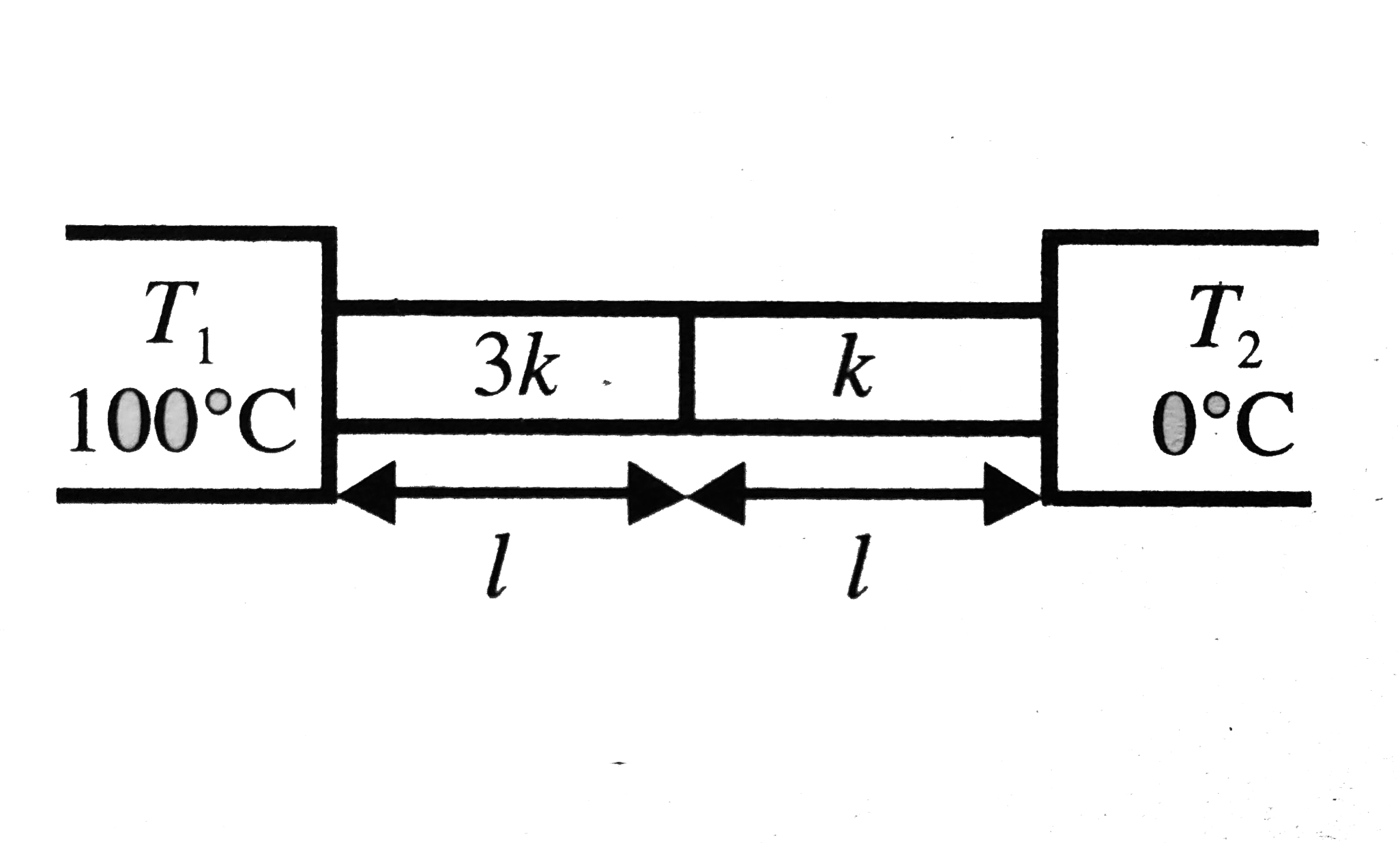
Two rods A and B of same length and cross-sectional area are connected in series and a temperature difference of 100∘C is maintained across the combination as shoen in Fig. If the thermal conductivity of the rod A is 3 k and that of rod B is k, Then
i.Determine the thermal resistance of each rod.
ii. determine the heat current flowing through each rod.
iii. determine the heat current flowing through each rod.
iv. plot the variation of temperature along the length of the rod.
View SolutionOne end of a uniform brass rod 20 cm long and 10cm2 cross-sectional area is kept at 100∘C. The other end is in perfect thermal contact with another rod of identical cross-section and length 10 cm. The free end of this rod is kept in melting ice and when the steady state has been reached, it is found that 360 g of ice melts per hour. Calculate the thermal conductivity of the rod, given that the thermal conductivity of brass is 0.25cal/scm∘CandL=80cal/g.
View SolutionTwo identical conducting rods AB and CD are connected to a circular conducting ring at two diametrically opposite points B and C, the radius of the ring is equal to the length of rods AB and CD. The area of cross-section, thermal conductivity of the rod and ring are equal. points A and D are maintained at temperatures of 100∘C and 0∘C. temperature at poimt C will be

View SolutionThe thermal conductivity of graphite along an axis in the plane of hexagonal rings is
View SolutionTwo rods A and B of different materials are welded together as shown in figure. Their thermal conductivities are K1 and K2. The thermal conductivity of the composite rod will be

View SolutionA cylindrical rod with one end in a steam chamber and the other end in ice results in melting of 0.1 g of ice per second. If the rod is replaced by another with half the length and double the radius of the first and if the thermal conductivity of material of second rod is 1/4 that of first, the rate at which ice melts in g/s will be
View SolutionExplain Lee's disc method of finding the thermal conductivity of a bad conductor.
View SolutionDescribe an experiment to determine the coefficient of thermal conductivity of a good conductor by Searle's method.
View Solution
