A circular curve of a highway is designed for traffic moving at 72 km/h. if the radius of the curved path is 100 m, the correct angle of banking of the road should be given by:
tan−1(25)
tan−1(35)
tan−1(15)
tan−1(14)
The correct Answer is:A
To solve the problem of finding the correct angle of banking of the road for a circular curve designed for traffic moving at 72 km/h with a radius of 100 m, we can follow these steps:
Step 1: Convert the speed from km/h to m/s
The speed given is 72 km/h. To convert this speed into meters per second (m/s), we use the conversion factor:
Speed in m/s=Speed in km/h×518
Calculating:
Speed in m/s=72×518=20 m/s
Step 2: Use the formula for banking angle
The formula for the tangent of the banking angle (θ) for safe turning is given by:
tan(θ)=V2Rg
Where:
- V is the speed (20 m/s),
- R is the radius of the curve (100 m),
- g is the acceleration due to gravity (approximately 10 m/s2).
Step 3: Substitute the values into the formula
Now we substitute the values into the formula:
tan(θ)=(20)2100×10
Calculating:
tan(θ)=4001000=0.4
Step 4: Calculate the angle θ
To find the angle θ, we take the arctangent (inverse tangent) of 0.4:
θ=tan−1(0.4)
Using a calculator or trigonometric tables, we find:
θ≈21.8∘
Step 5: Conclusion
Thus, the correct angle of banking of the road should be approximately 21.8∘.
---
The speed given is 72 km/h. To convert this speed into meters per second (m/s), we use the conversion factor:
The formula for the tangent of the banking angle (θ) for safe turning is given by:
- V is the speed (20 m/s),
- R is the radius of the curve (100 m),
- g is the acceleration due to gravity (approximately 10 m/s2).
Now we substitute the values into the formula:
To find the angle θ, we take the arctangent (inverse tangent) of 0.4:
Thus, the correct angle of banking of the road should be approximately 21.8∘.
Topper's Solved these Questions
- CIRCULAR MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - CIRCULAR MOTIONEXERCISE - Match the columns
3 Videos
- CIRCULAR MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - CIRCULAR MOTIONEXERCISE - Medical entrances s gallery
19 Videos
- CIRCULAR MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - CIRCULAR MOTIONEXERCISE - Check point
45 Videos
- CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONBOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONEXERCISE - Level 2 Subjective
21 Videos
- COMMUNICATION SYSTEMBOOK - DC PANDEY ENGLISHCHAPTER - COMMUNICATION SYSTEMEXERCISE - Only One Option is Correct
27 Videos
Similar Questions
For traffic moving at 60km/h if the radius of the curve is 0.1km what is the correct angle of banking of the road Given g=10m/s2 .
View SolutionA circular track of radius 600 m is tio be designed for cars at an average speed of 180 km/hr. What should be the angle of banking of the track?
View Solution
Knowledge Check
For traffic moving at 60 km/hour along a circular track of radius 0.1 km, the correct angle of banking is
A{(60)2/0.1} kmBtan−1[(50/3)2100×9.8]Ctan−1[100×9.8(50/3)2]Dtan−1√(60×0.1×9.8)
Check by dimensions whether the equation tanθ=rgv2 is correct.
Here, r = radius of curvature of path, g = acceleration due to gravity
v = velocity of body moving on the curved path, θ= angle of banking of the road
View SolutionAn airforce plane is ascending vertically at the rate of 100 km/h. If the radius of the earth is rkm, how fast is the area of the earth, visible from the plane, increasing at 3 minutes after it started ascending? Given that the visible area A at height h is given by A=2πr2hr+h .
View SolutionAn airforce plane is ascending vertically at the rate of 100 km/h. If the radius of the earth is rkm, how fast is the area of the earth, visible from the plane, increasing at 3 minutes after it started ascending? Given that the visible area A at height h is given by A=2πr2hr+h .
View SolutionA car is moving on a circular road which is rough and banked at angle . If radius of circular track is R then. Choose correct statement:
View SolutionA cyclist is moving on a smooth horizontal curved path of radius of curvature 10m.with a speed 10 ms−1. Then his angle of leaning is
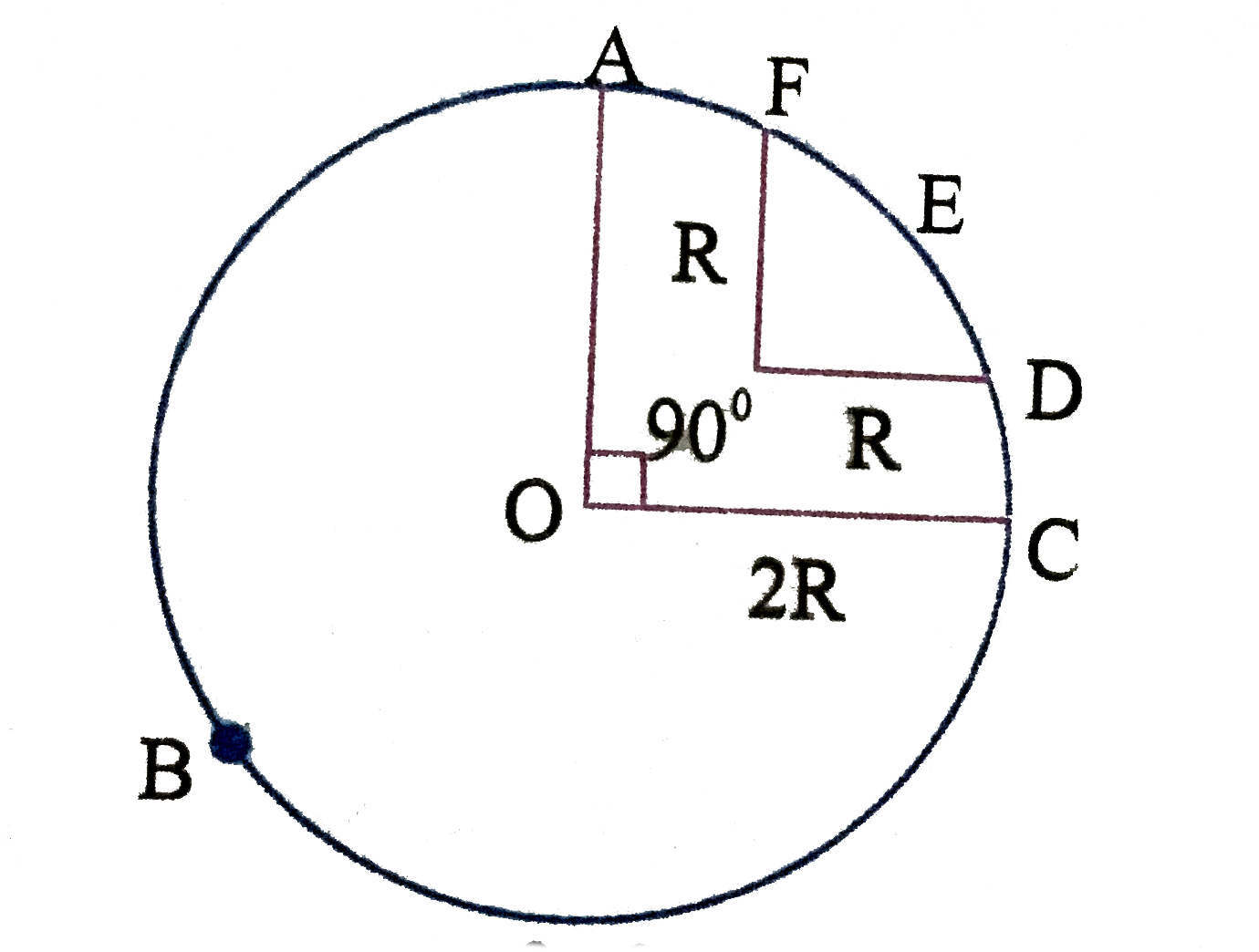
View SolutionA racing car travels on a track (without banking) ABCDEFA.ABC is a circular arc of radius 2R.CD and FA are straight paths of length R and DEF is a circular arc of radius R=100m. The co-efficient of friction on the road is ¼=0.1. the maximum speed of the car is 50ms−1. Find the minimum time for completing one round.
 .
.
View SolutionA circular road of radius r is banked for a speed v=40 km/hr. A car of mass m attempts to go on the circular road. The firctioncoefficient between the tyre and the road is negligible.
View Solution
