A particle of mass 2 kg is moving along a circular path of radius 1 m. If its angular speed is 2π rad s−1, the centripetal force on it is
4πN
8πN
4π4N
8π2N
The correct Answer is:D
To find the centripetal force acting on a particle moving in a circular path, we can use the formula:
Fc=mω2r
where:
- Fc is the centripetal force,
- m is the mass of the particle,
- ω is the angular speed,
- r is the radius of the circular path.
1. Identify the given values:
- Mass of the particle, m=2kg
- Radius of the circular path, r=1m
- Angular speed, ω=2πrad/s
2. Substitute the values into the centripetal force formula:
Fc=mω2r
Fc=2×(2π)2×1
3. Calculate ω2:
(2π)2=4π2
4. Now substitute ω2 back into the equation:
Fc=2×4π2×1
Fc=8π2
5. Final result:
The centripetal force Fc is:
Fc=8π2N
Conclusion:
The centripetal force acting on the particle is 8π2N.
---
- Fc is the centripetal force,
- m is the mass of the particle,
- ω is the angular speed,
- r is the radius of the circular path.
- Mass of the particle, m=2kg
- Radius of the circular path, r=1m
- Angular speed, ω=2πrad/s
Fc=mω2r
Fc=2×(2π)2×1
(2π)2=4π2
Fc=2×4π2×1
Fc=8π2
The centripetal force Fc is:
Fc=8π2N
The centripetal force acting on the particle is 8π2N.
Topper's Solved these Questions
- CIRCULAR MOTIONBook:DC PANDEY ENGLISHChapter:CIRCULAR MOTIONExercise:Taking it together
Explore 67 Videos
- CIRCULAR MOTIONBook:DC PANDEY ENGLISHChapter:CIRCULAR MOTIONExercise:Match the columns
Explore 3 Videos
- CIRCULAR MOTIONBook:DC PANDEY ENGLISHChapter:CIRCULAR MOTIONExercise:Integer
Explore 7 Videos
- CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONBook:DC PANDEY ENGLISHChapter:CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONExercise:Level 2 Subjective
Explore 21 Videos
- COMMUNICATION SYSTEMBook:DC PANDEY ENGLISHChapter:COMMUNICATION SYSTEMExercise:Only One Option is Correct
Explore 27 Videos
Similar Questions
A particle of mass m is rotating in a plane in circular path of radius r. Its angular momentum is L. The centripetal force acting on the particle is
View SolutionSpeed of an object moving in cirular path of radius 10 m with angular speed 2 rad/s is
View SolutionA particle of mass m is moving on a circular path of radius r with uniform speed v , rate of change of linear momentum is
View SolutionA particle of mass 'm' is moving on a circular path of radius 'r' with uniform speed 'v'. Rate of change of linear momentum is
View SolutionA particle is revolving in a circular path of radius 2 m with constant angular speed 4 rad/s. The angular acceleration of particle is
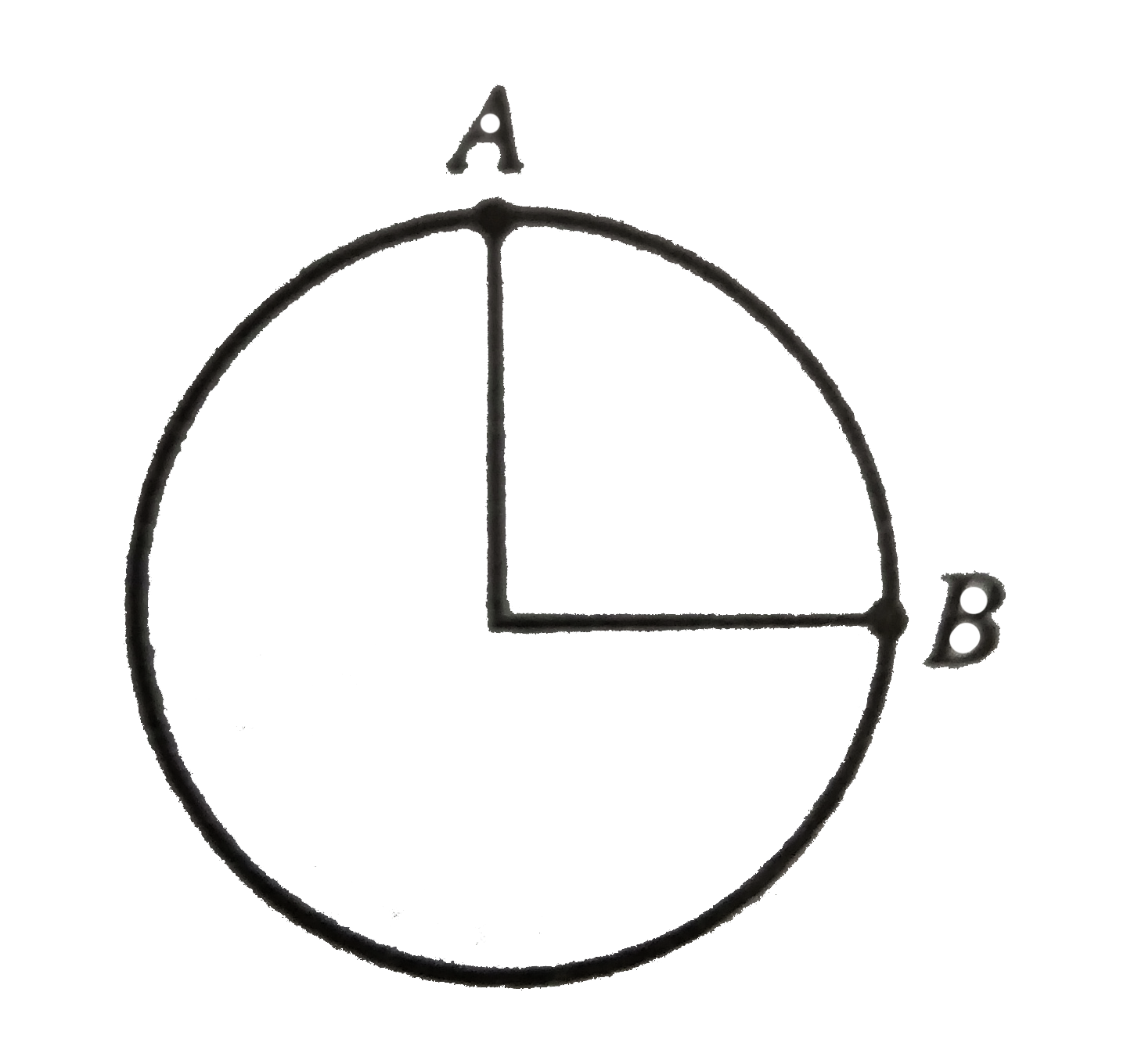
View SolutionA particle is moving in a circular path of radius 1 m. under the action of a centripetal force, the speed √2πms−1 of the particle is constant. Find the average of the velocity (inms−1) between A and B.
View SolutionA particle of mass 1 kg moves in a circular path of radius 1 m such that its speed varies with time as per equation v=3t2m/s where time t is in seconds. The power delivered by the force acting on the paritcle at t=1s, is :−
View SolutionA car of mass 1000 kg is moving with a speed of 40ms−1 on a circular path of radius 400m. If its speed is increasing at the rate of 3ms−2 the total force acting on the car is
View SolutionA particle is moving on a circular path of radius 1.5m at a constant angular acceleration of 2rad/s2. At the instant t=0, angular speed is 60/π rpm. What are its angular speed, angular displacement, linear velocity, tangential acceleration and normal acceleration and normal acceleration at the instant t=2s.
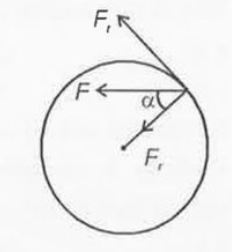
View SolutionA particle of mass m is moving in a circle of radius (r) with changing speed (v) the direction of centripetal force and tangential force are shown below the value of α is
View Solution

