PROGRESSIVE WAVES
phase difference between displacement and accleration of particle is zero
Phase difference bwteen displacement and acceleration of particle is π
phase difference between between displacement and velocity of particle is π/2
phase difference between velocity and acceleration of particle is π/2
The correct Answer is:B, C, D
Step by step video & image solution for PROGRESSIVE WAVES by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Related Playlists
- BOOK - DC PANDEY ENGLISHCHAPTER - WAVE MOTIONEXERCISE - Comprehion Type Questions20videos
WAVE MOTION
- BOOK - DC PANDEY ENGLISHCHAPTER - WAVE MOTIONEXERCISE - Matrix Matching16videos
WAVE MOTION
- BOOK - DC PANDEY ENGLISHCHAPTER - WAVE MOTIONEXERCISE - ONLY ONE OPTION IS CORRECT62videos
WAVE MOTION
- BOOK - DC PANDEY ENGLISHCHAPTER - VECTORSEXERCISE - Medical enrances gallery9videos
VECTORS
- BOOK - DC PANDEY ENGLISHCHAPTER - WORK, ENERGY & POWEREXERCISE - Level 2 Comprehension Based2videos
WORK, ENERGY & POWER
Similar Questions
WHICH OF THE FOLLOWING FUNCTIONS OF X AND T REPRESENTS A PROGRESSIVE WAVE ?
View Solution(A): In a mechanical progressive wave, energy is transferred from one point to the other.
(R): In a mechanical progressive wave energy transfer takes place because of the coupling through elastic forces between neighbouring oscillating particles of the medium.View Solution(A): In a progressive wave particle velocity and wave velocity are same.
(R): In a stationary wave energy is not confined to a limited region only.View SolutionIf the equation of progressive wave is given by y=4sinπ[t5−x9+π6] then, which of the following is correct ? (Assume SI units )
View SolutionAssertion:- Transvers waves are produced in a very long string fixed at one end. Near the free end only progressive wave is observed.
Reason:- Energy of reflected wave does does not reach the free end.View SolutionTwo plane progressive waves having the same wavelength λ And same frequencies with intensities 9I0 and 4I0 Suprimpose. Resulting intensity when the path difference between waves become λ4 is
View SolutionThe equation of the progressive wave, where t is the time in second , x is the distance in metre is y=Acos240(t−x12) . The phase difference ( in SI units ) between two position 0.5 m apart is
View Solutionthe same progressive wave is reprsented by two group I and II. Graoup I shows how the displacement 'y' varies with the distance x along the wave at a given time. Graph II shows how y varies with time t at a given point on the wave. The ratio of measurements AB to CD, marked on the curvse m repersents.
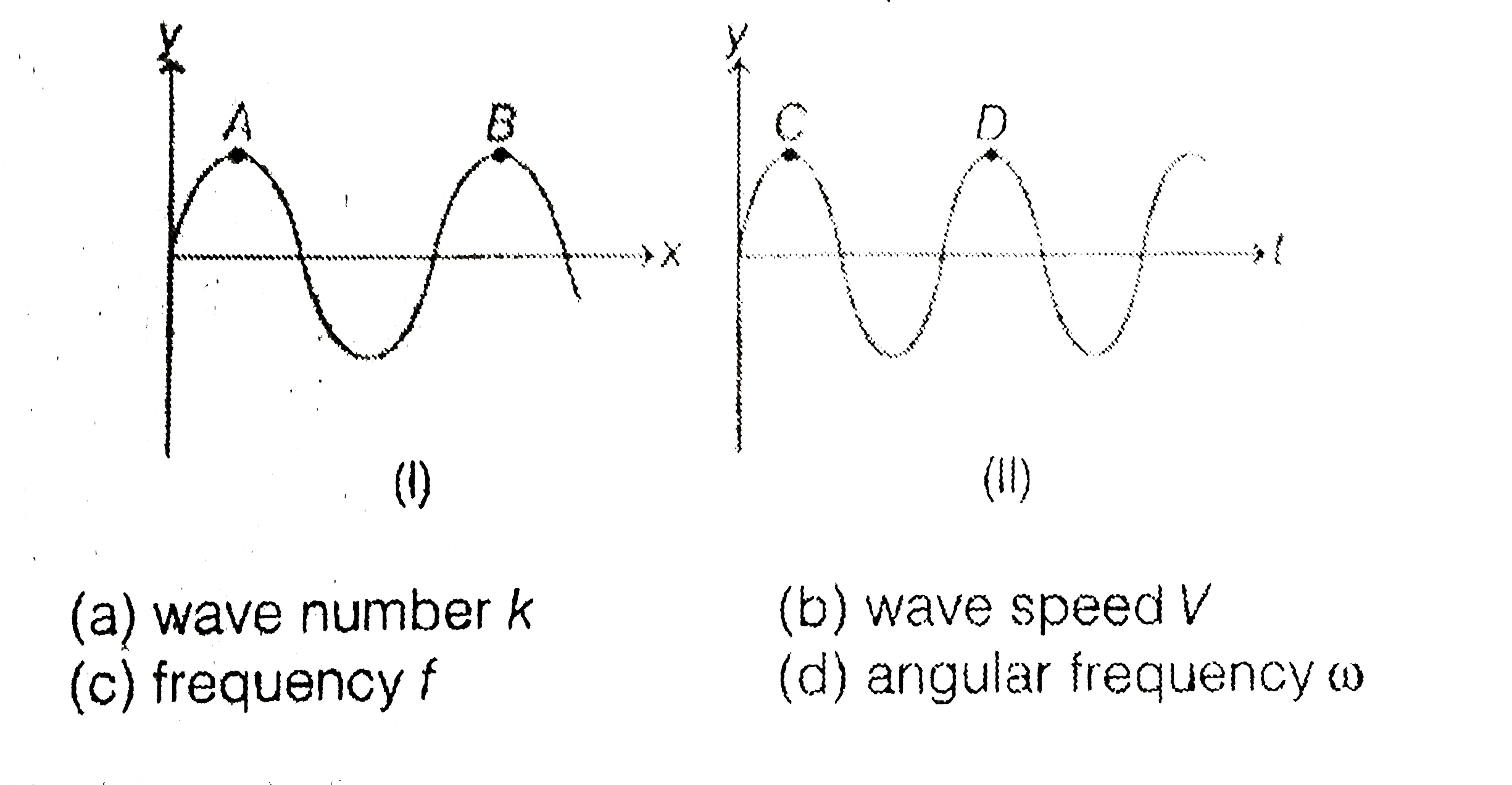 View Solution
View Solution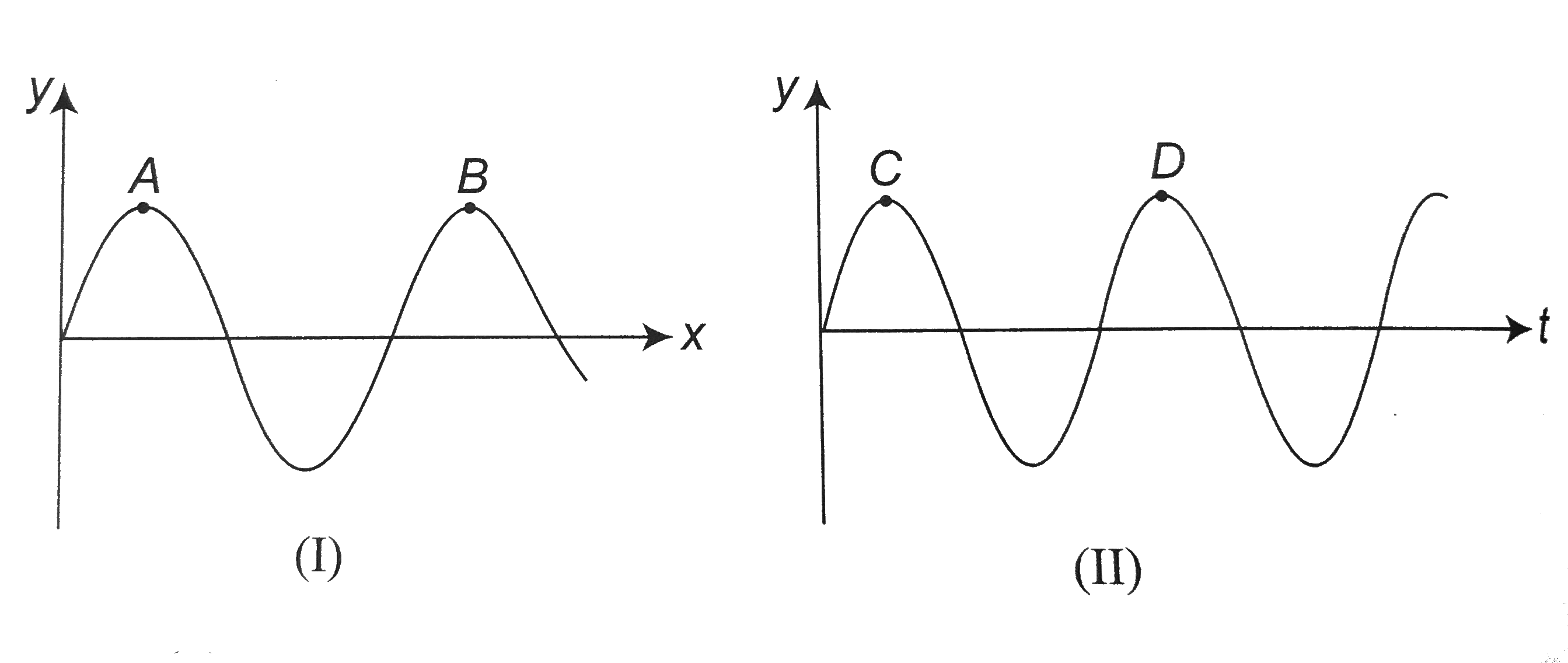
The same progressive wave is represented by two graphs I and II. Graph I shows how the displacement y varies with the distance x along the wave at a given time. Graph II shows how y varies with time t at a given point on the wave. The ratio of measurements AB to CD, marked on the curves represents:View Solutionstatement I: The intensity of a plane progressive wave does not change with change in distance from the source.
Statement II: The wavefronts associated with a plane progressive wave are planar.View Solution


