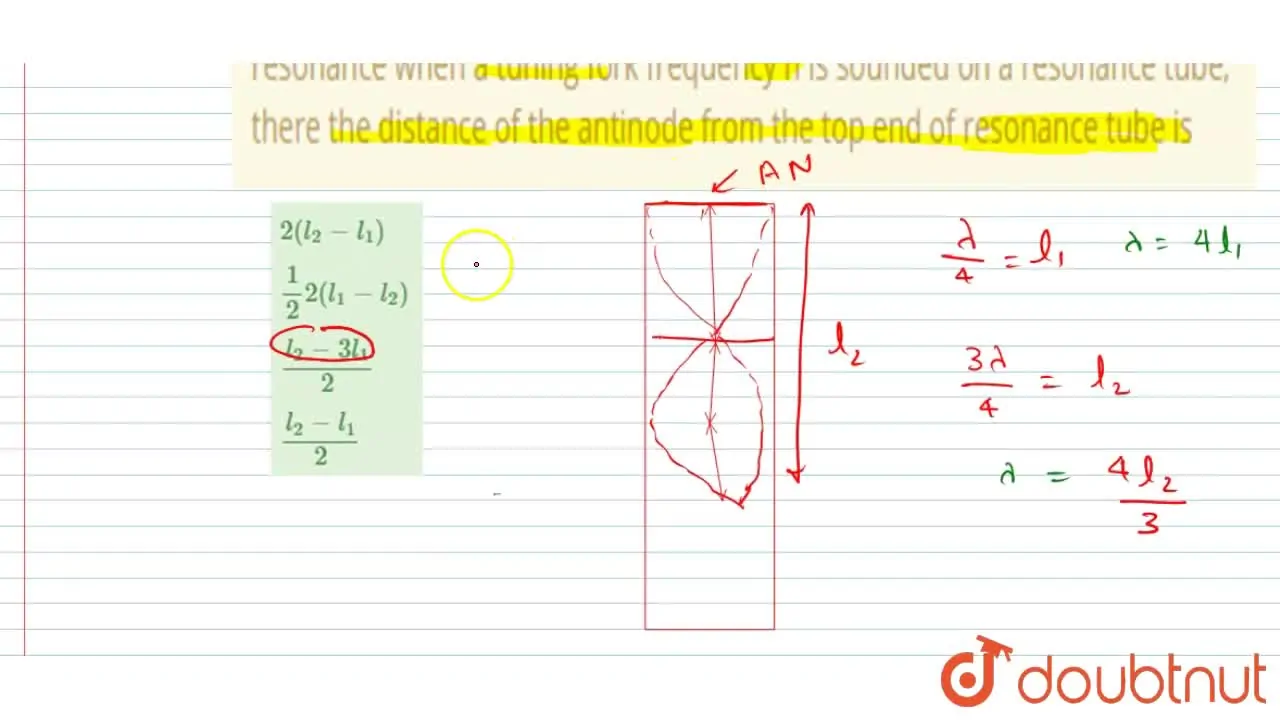
If l1andl2 are the lengths of air column for the first and second resonance when a tuning fork frequency n is sounded on a resonance tube, there the distance of the antinode from the top end of resonance tube is
2(l2−l1)
122(l1−l2)
l2−3l12
l2−l12
The correct Answer is:C
Step by step video & image solution for If l_(1) and l_(2) are the lengths of air column for the first and second resonance when a tuning fork frequency n is sounded on a resonance tube, there the distance of the antinode from the top end of resonance tube is by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Related Playlists
- BOOK - DC PANDEY ENGLISHCHAPTER - WAVE MOTIONEXERCISE - More Than One Option is Correct23videos
WAVE MOTION
- BOOK - DC PANDEY ENGLISHCHAPTER - WAVE MOTIONEXERCISE - Comprehion Type Questions20videos
WAVE MOTION
- BOOK - DC PANDEY ENGLISHCHAPTER - WAVE MOTIONEXERCISE - JEE MAINS50videos
WAVE MOTION
- BOOK - DC PANDEY ENGLISHCHAPTER - VECTORSEXERCISE - Medical enrances gallery9videos
VECTORS
- BOOK - DC PANDEY ENGLISHCHAPTER - WORK, ENERGY & POWEREXERCISE - Level 2 Comprehension Based2videos
WORK, ENERGY & POWER
Similar Questions
If l1andl2 are the lengths of air column for two air column for two consecutive resonance position when a turning fork of frequency f is sounded in a resonance tube, then end correction is :
View SolutionAn open pipe resonates with a tuning fork of frequency 500Hz . It is observed that two successive notes are formed at distance 16and46cm from the open end. The speed of sound in air in the pipe is
View SolutionThe end correction ( e) is (l1 = length of air column at first resonance and l2 is length of air column at second resonance).
View SolutionA tuning fork of frequency 500HZ is sounded on a resonance tube . The first and second resonances are obtained at 17cm and 52cm . The velocity of sound is
View SolutionA student performed the experiment to measure the speed of sound in air using resonance air-column method. Two resonances in the air-column were obtained by lowering the water level. The resonance with the shorter air-column is the first resonance and that with the longer air-column is the second resonance. Then,
A. the intensity of the sound heard at the first resonance was more than at the second resonance
B. the prongs of the tuning fork were kept in a horizontal plane above the resonance tube
C. the ampitude of vibration of the end of the prongs is typically around 1cm
D. the length of the air-column at the first resonance was somewhat than 1/4 th of the wavelength of the sound in air.View SolutionThe temperature of an organ pipe when it is in resonance with a tuning fork is increased. How does the resonant length change?
View SolutionIn the resonance tube experiment , the first resonance is heard when length of air column is l1 and second resonance is heard when length of air column is l2. What should be the minimum length of the tube so that third resonance can also be heard.
View SolutionA tuning fork of frequency 500Hz when sounded on the mouth of resonance tube the lengths of air column for first and second resonance are recorded as 10cm and 40cm respectively. The room temperature is 20°C. The velocity of sound at the room temperature obtained from the explanation is
View SolutionThe first resonance length of a resonance tube is 40cm and the second resonance length is 122cm . The third resonance length of the tube will be
View SolutionA closed organ pipe of length L is in resonance with a tuning fork. If a hole is made in the pipe at a distance L4 from closed - end, it will be in resonance again, when:
View Solution