Two particles A and B of mass 1 kg and 2 kg respectively are projected in the direction shown in figure with speeds uA=200ms−1 and uB=50ms−1. Initially they were 90 m apart. Find the maximum height attained by the center of mass of the particles. Assume acceleration due to gravity to be constant. (Take, g=10ms−2.
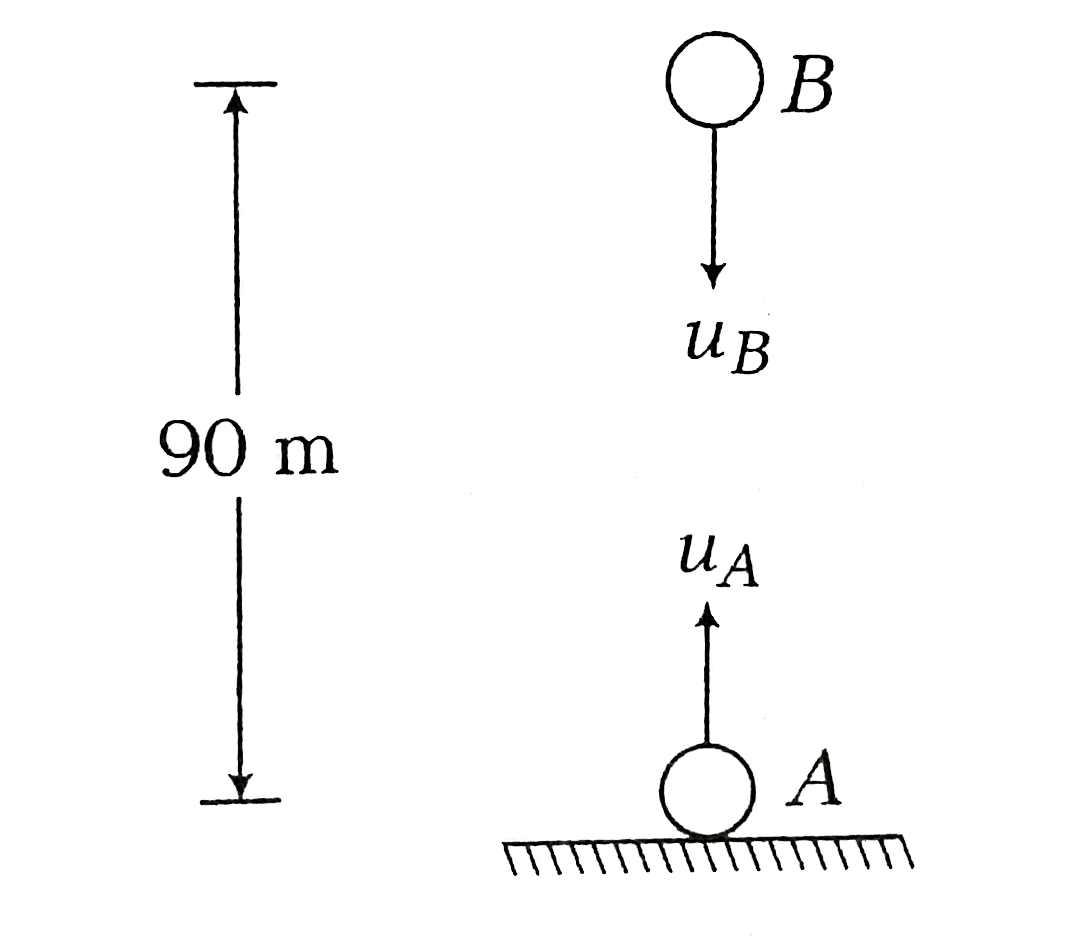
Using, mArA=mBrB or 1(rA)=2(rB)
or rA=2rB..................(i)
and rA+rB = 90 m ..........................(ii)
Solving thest two equations, we get
rA=60 m and rB =30 m
i.e., CM is at height 60 m from the ground at time t=0.
Further, aCM = mAaA+mBaBmA+mB= g = 10ms−1 (downwards)
as aA = aB) = g (downwards)
uCM = mAuA+mBuBmA+mB
1(200)−2(50)1+2=1003ms−1 (upwards)
Let h be the height attained by CM beyond 60m. Using
v2CM=v2CM+2aCMh
or 0=(1003)2−(2)(10(h)
or h=(100)2180=55.55m
Therefore, maximum height attained by the center of mass is H=60 + 55.55 = 115.55m
Topper's Solved these Questions
- CENTRE OF MASSBOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - Check points
50 Videos
- CENTRE OF MASSBOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - Taking it together
73 Videos
- CALORIMETRY AND HEAT TRANSFERBOOK - DC PANDEY ENGLISHCHAPTER - CALORIMETRY AND HEAT TRANSFEREXERCISE - Medical entrance s gallery
38 Videos
- CENTRE OF MASS, IMPULSE AND MOMENTUMBOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASS, IMPULSE AND MOMENTUMEXERCISE - Comprehension type questions
15 Videos
Similar Questions
Two particles A and B of masses 1kg and 2kg respectively are projected in the directions shown in figure with speeds uA=200m/s and uB=50m/s. Initially they were 90m apart. They collide in mid air and stick with each other. Find the maximum height attained by the centre of mass of the particles. Assume acceleration due to gravity to be constant.
(g=10m/s2)

View SolutionTwo block A and B of mass 50kg and 300kg respectively are placed as shown in figure. Coefficient of friction between all surface is 12
Then (take g=10m/s)
View SolutionThe maximum height attained by a ball projected with speed 20ms−1 at an angle 45∘ with the horizontal is [take g = 10ms−2]
View SolutionTwo particles A and B of mass 3kg and 2kg moving with speed 10m/s and 5m/s as shown in figure.
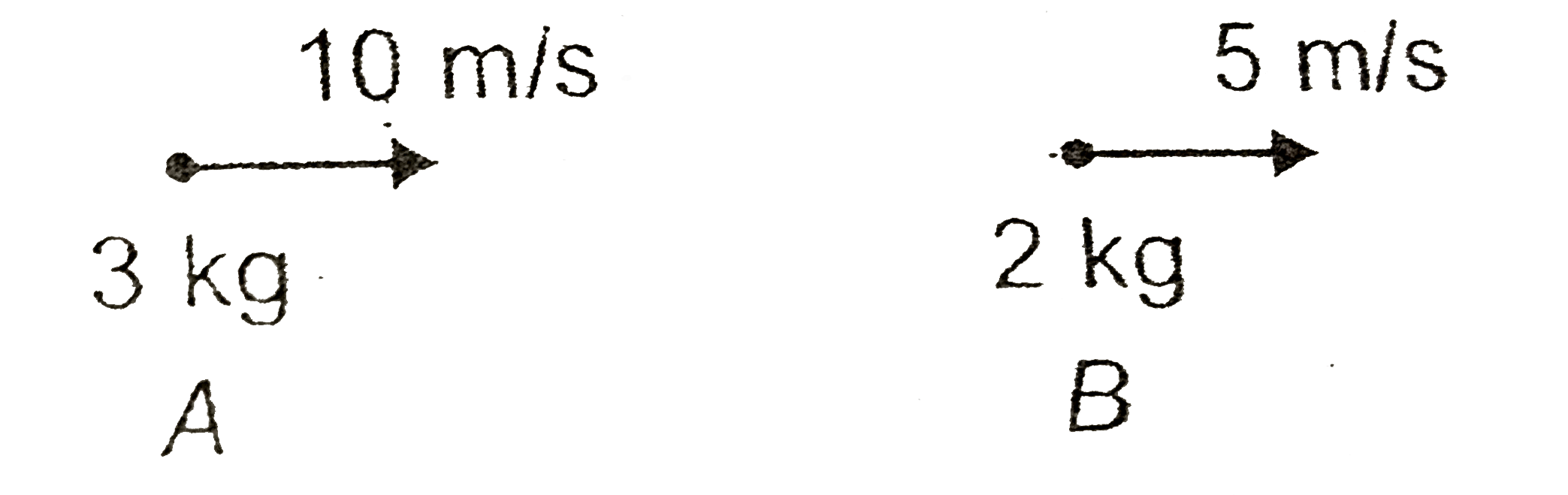
Kinetic energy of particle A when particle B has the maximum momentum
View SolutionTwo particles of masses 3kg and 2kg move due north and due east respectively with the velocities2ms−1and3ms−1. The magnitude and direction of the velocity of centre of mass is
View SolutionA ball is projected vertically upward with a speed of 50m/s. Find (a) the maximum height, (b) the time to reach the maximum height, (c) the speed at half the maximum height. Take g=10ms2.
View SolutionTwo particles A and B of mass 3kg and 2kg moving with speed 10m/s and 5m/s as shown in figure.
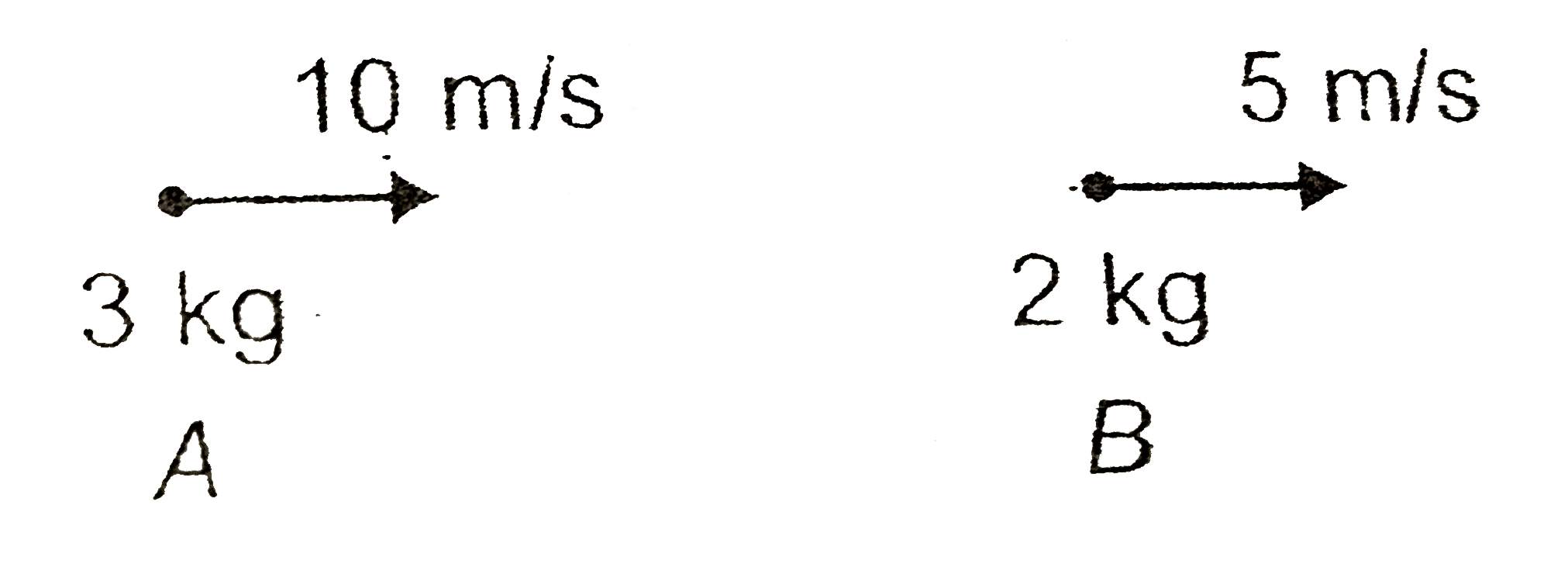
Find the maximum momentum that particle B can have after collision with A
View SolutionIf unit of mass is taken as 1 kg, of time a 1 minute and that acceleration due to gravity is taken as 9.81ms−2 . What is the unit of energy?
View SolutionTwo particles A and B of mass 3kg and 2kg moving with speed 10m/s and 5m/s as shown in figure.
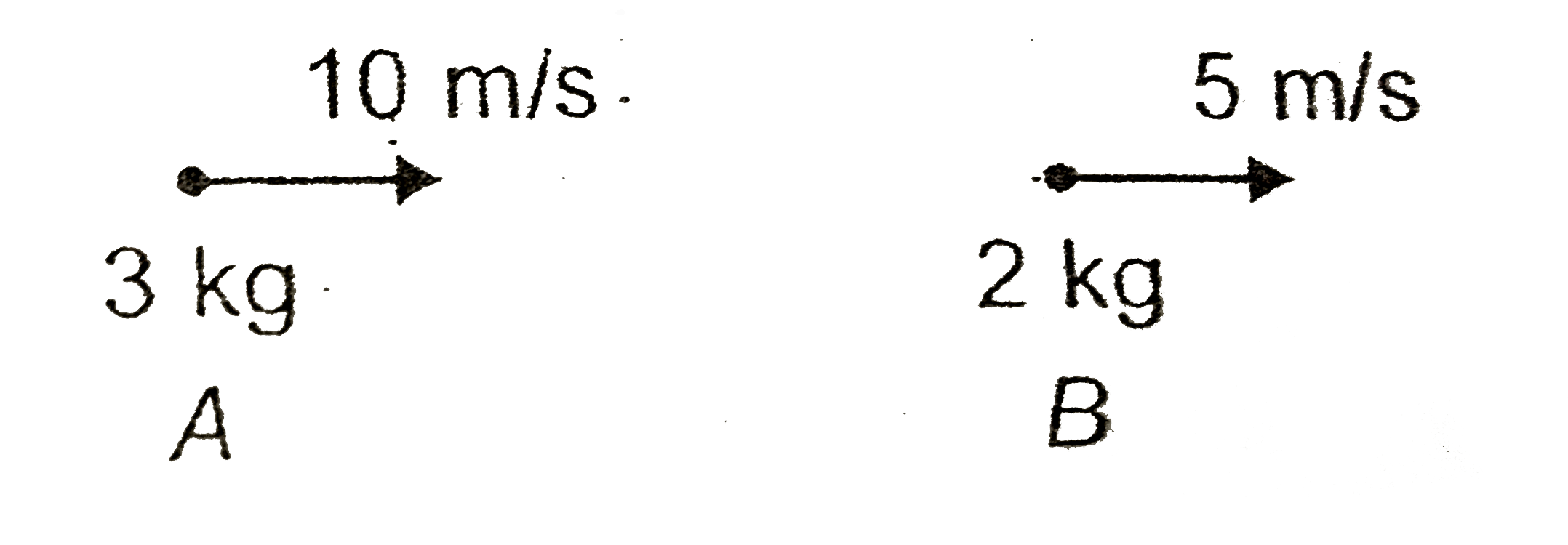
Find the maximum momentum that particles A can have after collision with B.
View SolutionThree particles of masses 1kg,2kg and 3kg are situated at the corners of an equilateral triangle move at speed 6ms−1,3ms−1 and 2ms−1 respectively. Each particle maintains a direction towards the particles at the next corners symmetrically. Find velocity of CM of the system at this instant
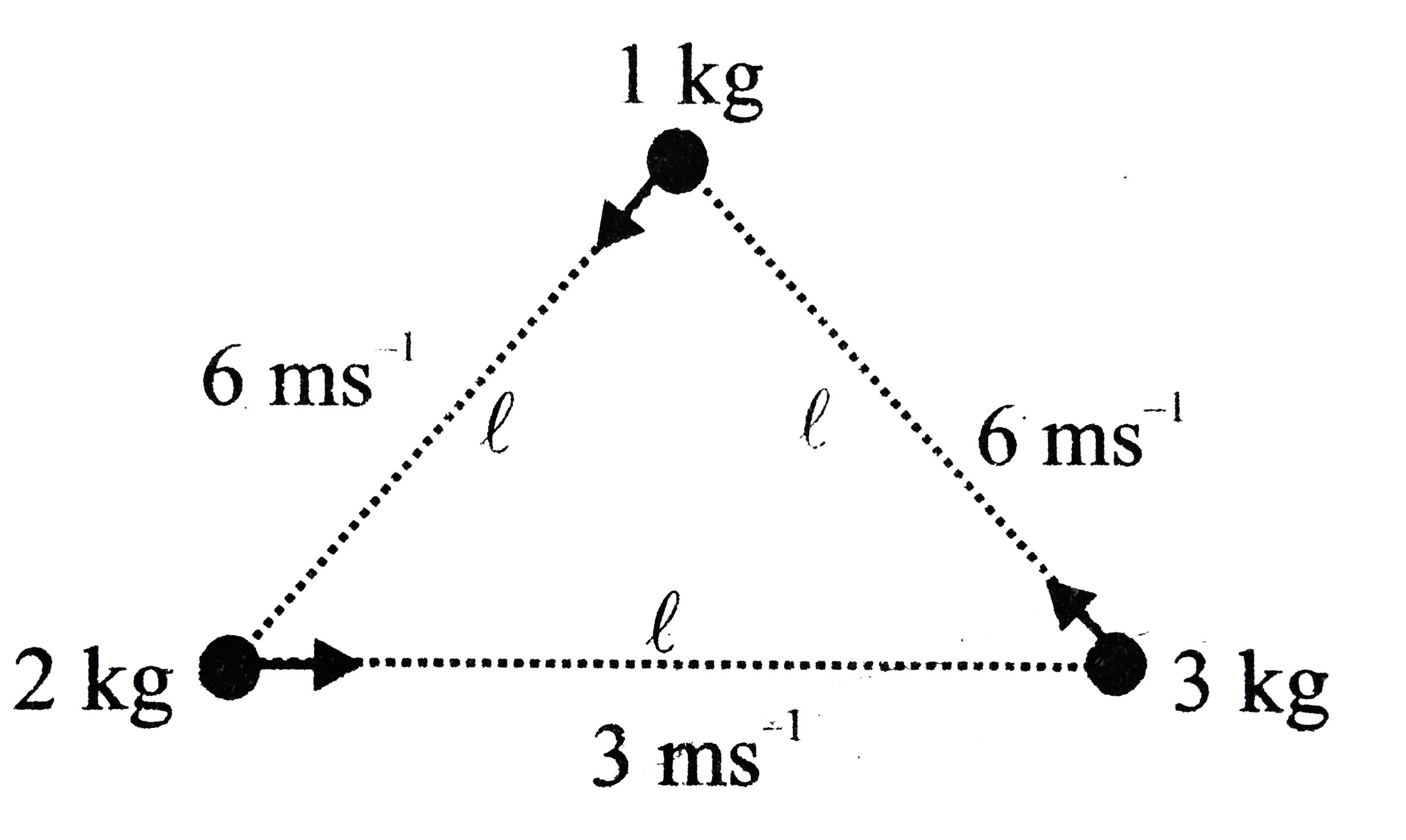
View Solution
