Maximum kinetic energy of a photoelectron is E when the wavelength of incident light is λ. If energy becomes four times when wavelength is reduced to one thrid, then work function of the metal is
3hcλ
hc3λ
hcλ
hc2λ
The correct Answer is:B
To solve the problem, we will follow these steps:
Step 1: Understand the relationship between energy, wavelength, and work function
The energy of a photon can be expressed as:
E=hν=hcλ
where h is Planck's constant, c is the speed of light, and λ is the wavelength of the incident light.
Step 2: Write the equation for the maximum kinetic energy of the photoelectron
The maximum kinetic energy (KE) of the photoelectron can be expressed as:
KE=E−ϕ
where ϕ is the work function of the metal.
Step 3: Set up equations for the two scenarios
1. For the first case, where the maximum kinetic energy is E and the wavelength is λ:
E=hcλ−ϕ(Equation 1)
2. For the second case, where the maximum kinetic energy becomes 4E and the wavelength is reduced to λ3:
4E=hcλ3−ϕ=3hcλ−ϕ(Equation 2)
Step 4: Substitute Equation 1 into Equation 2
From Equation 1, we can express E as:
E=hcλ−ϕ
Now, substituting this into Equation 2:
4(hcλ−ϕ)=3hcλ−ϕ
Step 5: Simplify the equation
Expanding the left side:
4hcλ−4ϕ=3hcλ−ϕ
Rearranging gives:
4hcλ−3hcλ=4ϕ−ϕ
This simplifies to:
hcλ=3ϕ
Step 6: Solve for the work function ϕ
Now, we can solve for ϕ:
ϕ=hc3λ
Final Answer
The work function of the metal is:
ϕ=hc3λ
---
The energy of a photon can be expressed as:
E=hν=hcλ
where h is Planck's constant, c is the speed of light, and λ is the wavelength of the incident light.
The maximum kinetic energy (KE) of the photoelectron can be expressed as:
KE=E−ϕ
where ϕ is the work function of the metal.
1. For the first case, where the maximum kinetic energy is E and the wavelength is λ:
E=hcλ−ϕ(Equation 1)
4E=hcλ3−ϕ=3hcλ−ϕ(Equation 2)
From Equation 1, we can express E as:
E=hcλ−ϕ
Now, substituting this into Equation 2:
4(hcλ−ϕ)=3hcλ−ϕ
Expanding the left side:
4hcλ−4ϕ=3hcλ−ϕ
Rearranging gives:
4hcλ−3hcλ=4ϕ−ϕ
This simplifies to:
hcλ=3ϕ
Now, we can solve for ϕ:
ϕ=hc3λ
The work function of the metal is:
ϕ=hc3λ
Topper's Solved these Questions
- MODERN PHYSICS - 1BOOK - DC PANDEY ENGLISHCHAPTER - MODERN PHYSICS - 1EXERCISE - Level 1 Subjective
40 Videos
- MODERN PHYSICS - 1BOOK - DC PANDEY ENGLISHCHAPTER - MODERN PHYSICS - 1EXERCISE - Level 2 Single Correct
22 Videos
- MODERN PHYSICS - 1BOOK - DC PANDEY ENGLISHCHAPTER - MODERN PHYSICS - 1EXERCISE - Level -1 Assertion And Reason
10 Videos
- MODERN PHYSICSBOOK - DC PANDEY ENGLISHCHAPTER - MODERN PHYSICSEXERCISE - Integer Type Questions
17 Videos
- MODERN PHYSICS - 2BOOK - DC PANDEY ENGLISHCHAPTER - MODERN PHYSICS - 2EXERCISE - Level 2 Subjective
10 Videos
Similar Questions
The KE of the photoelectrons is E when the incident wavelength is λ2. The KE becomes 2E when the incident wavelength is λ3. The work function of the metal is
View SolutionMaximum kinetic energy of photoelectrons from a metal
surface is K0 when wavelngth of incident light is λ. If wavelength is decreased
to λ∣2, the maximum kinetic energy of photoelectrons becomes
(a) =2K0 (b)>2K0 (c ) <2K0
View SolutionIf light of wavelength λ1 is allowed to fall on a metal , then kinetic energy of photoelectrons emitted is E1. If wavelength of light changes to λ2 then kinetic energy of electrons changes to E2. Then work function of the metal is
View SolutionThe kinetic energy of an electron is E when the incident wavelength is λ To increase ti KE of the electron to 2E, the incident wavelength must be
View SolutionThe maximum kinetic energy of photoelectron is doubled when the wavelength of light incident on the photosensitive changes from λ1 to λ2. Deduce expression for the threshold wavelength and work function for metals in terms of λ1 and λ2
View SolutionMaximum kinetic energy of photoelectrons emitted from a metal surface, when light of wavelength λ is incident on it, is 1 eV. When a light of wavelength λ3 is incident on the surfaces, maximum kinetic energy becomes 4 times. The work function of the metal is
View SolutionThe kinetic energy of the most energetic photoelectrons emitted from a metal surface is doubled when the wavelength of the incident radiation is reduced from λ1 to λ2 The work function of the metal is
View SolutionWhen the incident wavelengths are λ and λ/2 the kinetic energies of the emitted photo electrons are E and 2E. The work function of the metal is
View Solution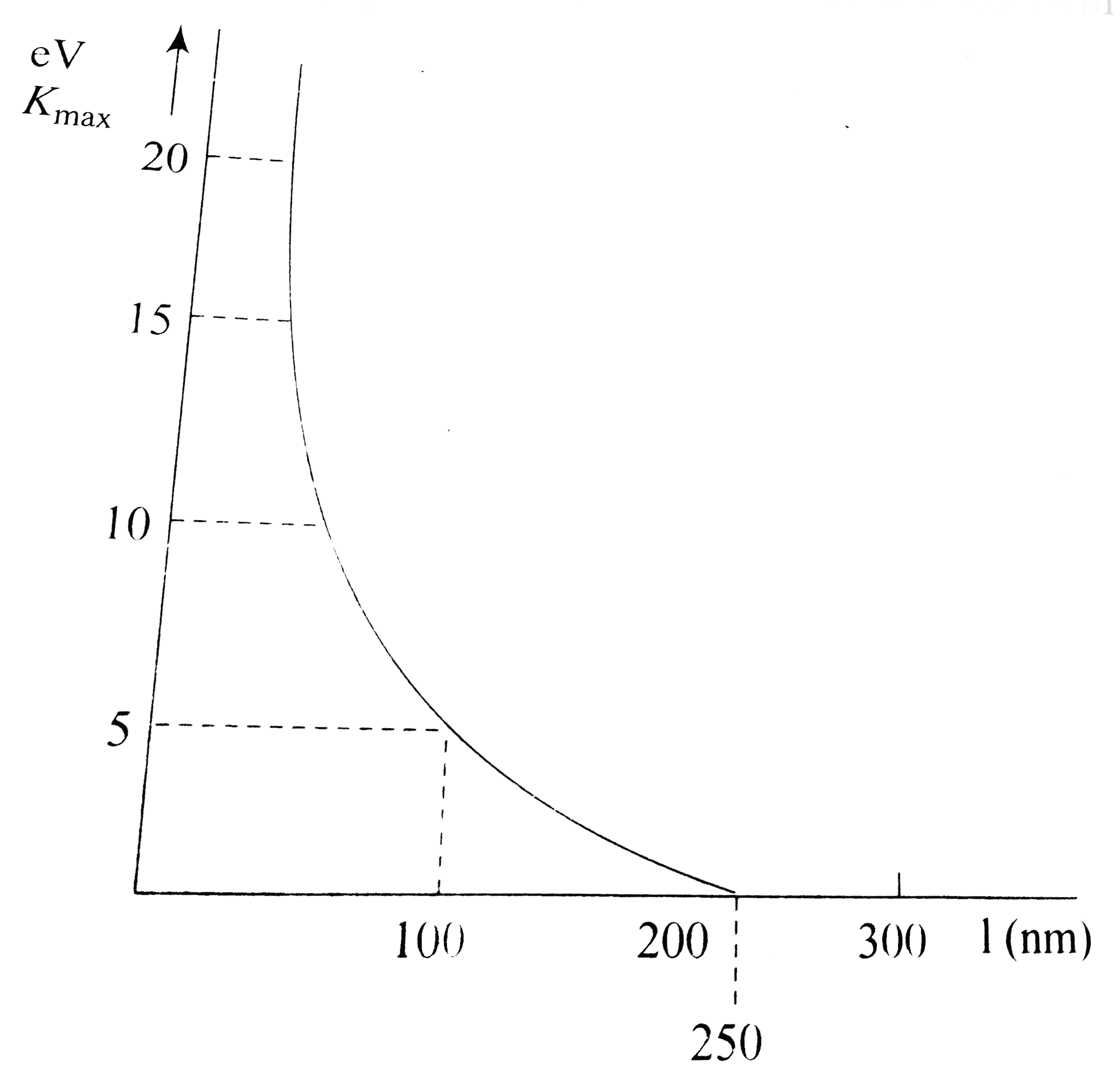
In a photoelectric effect experiment , the maximum kinetic energy of the ejected photoelectrons is measured for various wavelength of the incident light. Figure shows a graph of this maximum kinetic energy Kmax as a function of the wavelength λ of the light falling on the surface of the metal. Which of the following statement/i is/ are correct?
View SolutionIn an experiment of photo-electric effect, the graph of maximum kinetic energy Ek of the emitted photoelectrons versus the frequency v of the incident light is a straight line AB as shown in figure below :
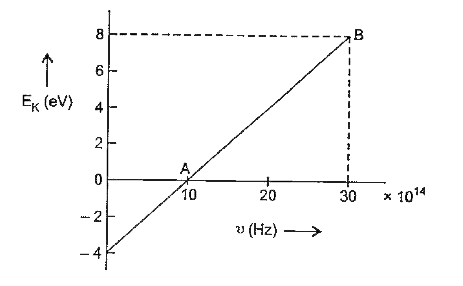
Work function of the metal.
View Solution
