A balloon is moving upwards with a speed of 20m/s. When it is at a height of 14 m from ground in front of a plane mirror in situation as shown in figure, a boy drops himself from the balloon. Find the time duration for which he will see the image of source S placed symmetrically before plane mirror during free fall.
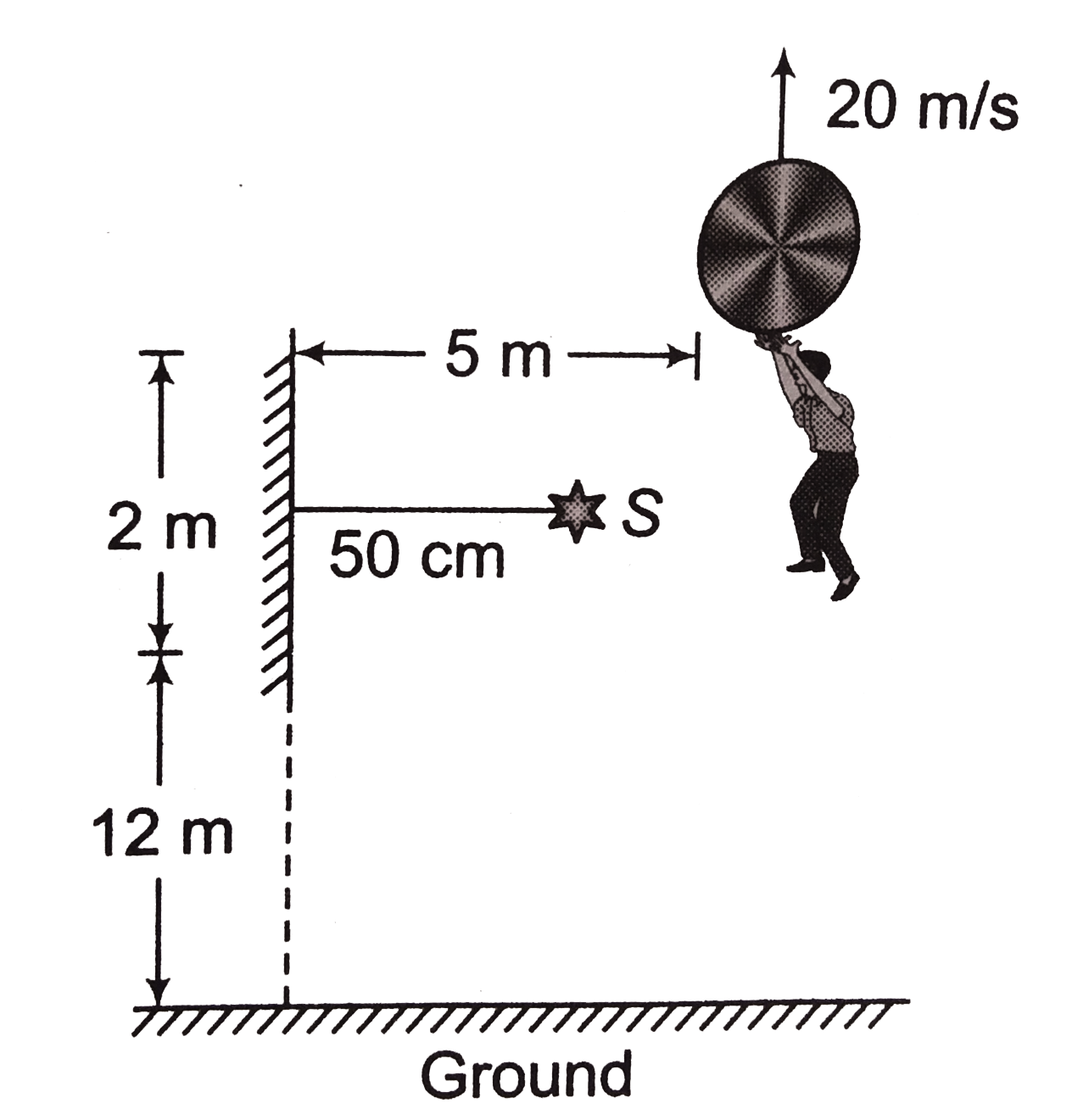
The correct Answer is:A
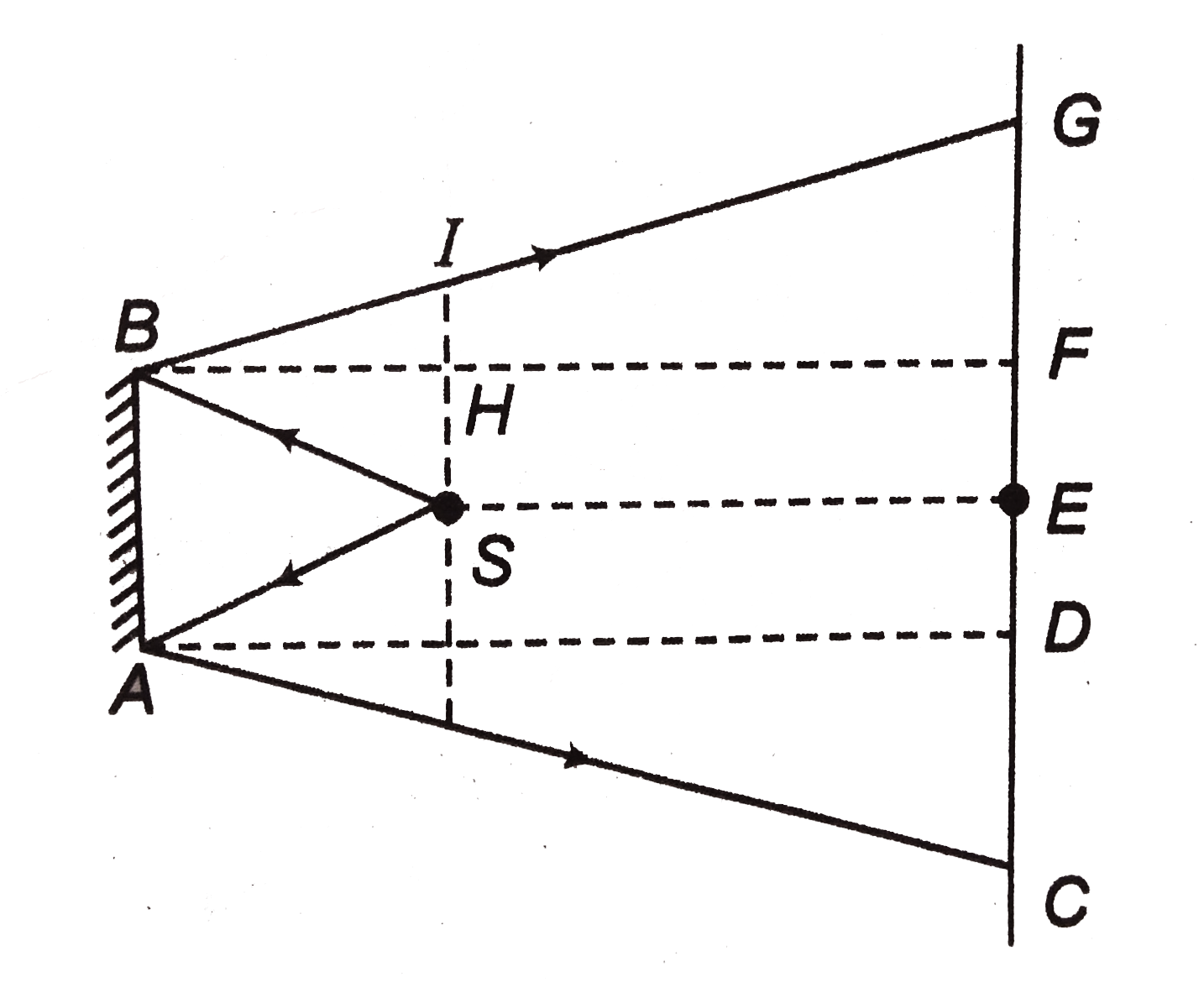
FGBF=IHBH=HSBH
∴FG=(BF)(HSBH)
=(5)(0.10.5)
FC=2+10=12m
The boy has dropped himself at point f. So, his velocity is 20m/s in upward direction. Let us from the time to move from F to topmost point and then from topmost point to point
C. from s=(ut)+(12)(at)2, we have
=−12=(20t)+(12)(−10)t2
Solving this equation we get, (t1)=4.53s.
Velocity of boy at point G,
v=√(202)−2×10×10
=14.4m/s(∴v2=u2−2gh)
Time taken to move the boy from G to topmost point and then from topmost point to G will be
(t2)=2vg=2.83s
∴ The required time is t=t1−t2=1.7s.
Topper's Solved these Questions
- REFLECTION OF LIGHTBook:DC PANDEY ENGLISHChapter:REFLECTION OF LIGHTExercise:Level 2 Comprehensive Based
Explore 4 Videos
- RAY OPTICSBook:DC PANDEY ENGLISHChapter:RAY OPTICSExercise:Medical entrance gallary
Explore 76 Videos
- REFRACTION OF LIGHTBook:DC PANDEY ENGLISHChapter:REFRACTION OF LIGHTExercise:Level 2 Subjective
Explore 21 Videos
Similar Questions
A person's eye is at a height of 1.5 m . He stands infront of a 0.3 m long plane mirror whose lower end is 0.8m above the ground. The length of the image he sees of himself is
View SolutionA body is dropped from a balloon meving up wigh a velocity of 4ms−2 when the balloon is at a height of 12.5 m from the ground.
The distance of separation between of separation between the body and the balloon after 5 is.
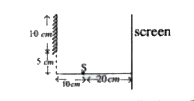
View SolutionA luminous point source s is placed between a plane mirror and a screen in the situation as shown in figure. Then the length of screen which will receive direct light as well as reflected light is
View SolutionA ball is thrown upwards from the ground with an initial speed of u. The ball is at height of 80m at two times, the time interval being 6 s. Find u. Take g=10m/s2.
View SolutionA ball is throuwn with a speed of 20 m//s from top of a buling 150 m high and simultaneously another ball is thrown vertically upward witn a speed of 30 m/s from the foot of the builing . Find the time when both the balls will meet (g=10m/s2)
View SolutionA balloon is going upwards with a constant velocity 15m/s. When the ballooon is at 50 m height, a stone is dropped outside from the balloon. How long will stone take to reach at the ground? (take g=10m/s2)
View SolutionA diverging lens of focal length 10cm is placed 10cm in front of a plane mirror as shown in Fig. Light from a very far away source falls on the lens. What is the distance of final image?

View SolutionA balloon is moving upwards with velocity 10m/s. It releases a stone which comes down to the ground in 11s. The height of the balloon from the ground at the moment when the stone was dropped is (g=10m/s2)
View SolutionA stone is dropped from a rising balloon at a height of 76 m above the ground and reaches the ground in 6s. What was the velocity of the balloon when the stone was dropped?
View SolutionA balloon carring a stone is moving vartically upward with velocity 12m/s. When the balloon is at height 64m, the stone is dropped. After how much time and with what velocity will it strike the ground?
View Solution