In an AC circuit, the power factor
is unity when the circuit contains an ideal resistance only
is unity when the circuit contains an ideal inductance only
is zero when the circuit contains an ideal resistance only
is zero when the circuit contains an ideal inductance only
The correct Answer is:A, D
To solve the question regarding the power factor in an AC circuit, we need to analyze the power factor formula and the conditions under which it takes specific values. The power factor (PF) is defined as:
Power Factor (PF)=cosϕ=R√R2+(XL−XC)2
Where:
- R is the resistance,
- XL is the inductive reactance,
- XC is the capacitive reactance.
1. Understanding Power Factor:
- The power factor is a measure of how effectively electrical power is being converted into useful work output. It is the cosine of the phase angle ϕ between the voltage and current in an AC circuit.
2. Case 1: Ideal Resistance Only:
- If the circuit contains only an ideal resistance, then XL=0 and XC=0.
- The power factor becomes:
cosϕ=R√R2+0=RR=1
- This means the power factor is unity (1) when the circuit contains only an ideal resistance. (Correct)
3. Case 2: Ideal Inductance Only:
- If the circuit contains only an ideal inductance, then R=0 and XC=0.
- The power factor becomes:
cosϕ=0√0+X2L=0
- This means the power factor is zero when the circuit contains only an ideal inductance. (Incorrect)
4. Case 3: Ideal Resistance Only (Revisited):
- As previously calculated, if the circuit contains only an ideal resistance, the power factor is 1. (Incorrect)
5. Case 4: Ideal Inductance Only (Revisited):
- As previously calculated, if the circuit contains only an ideal inductance, the power factor is 0. (Correct)
Conclusion:
- The correct statements regarding the power factor in the given options are:
- The power factor is unity (1) when the circuit contains an ideal resistance only.
- The power factor is zero (0) when the circuit contains an ideal inductance only.
- R is the resistance,
- XL is the inductive reactance,
- XC is the capacitive reactance.
- The power factor is a measure of how effectively electrical power is being converted into useful work output. It is the cosine of the phase angle ϕ between the voltage and current in an AC circuit.
- If the circuit contains only an ideal resistance, then XL=0 and XC=0.
- The power factor becomes:
cosϕ=R√R2+0=RR=1
- This means the power factor is unity (1) when the circuit contains only an ideal resistance. (Correct)
- If the circuit contains only an ideal inductance, then R=0 and XC=0.
- The power factor becomes:
cosϕ=0√0+X2L=0
- This means the power factor is zero when the circuit contains only an ideal inductance. (Incorrect)
- As previously calculated, if the circuit contains only an ideal resistance, the power factor is 1. (Incorrect)
- As previously calculated, if the circuit contains only an ideal inductance, the power factor is 0. (Correct)
- The correct statements regarding the power factor in the given options are:
- The power factor is unity (1) when the circuit contains an ideal resistance only.
- The power factor is zero (0) when the circuit contains an ideal inductance only.
Topper's Solved these Questions
- ALTERNATING CURRENTBOOK - DC PANDEY ENGLISHCHAPTER - ALTERNATING CURRENTEXERCISE - Level 2 Comprehension
6 Videos
- ALTERNATING CURRENTBOOK - DC PANDEY ENGLISHCHAPTER - ALTERNATING CURRENTEXERCISE - Level 2 Subjective
10 Videos
- ALTERNATING CURRENTBOOK - DC PANDEY ENGLISHCHAPTER - ALTERNATING CURRENTEXERCISE - Level- 2 Single Correct
18 Videos
- ATOMSBOOK - DC PANDEY ENGLISHCHAPTER - ATOMSEXERCISE - MEDICAL ENTRANCES GALLERY
42 Videos
Similar Questions
The potential differences across the resistance, capacitance and inductance are 80V,40V and 100V respectively in an L−C−R circuit. The power factor of this circuit is
View SolutionGiven below are two electric circuits A and B
Calculate the ratio of power factor of the circuit B to the power factor of circuit A.
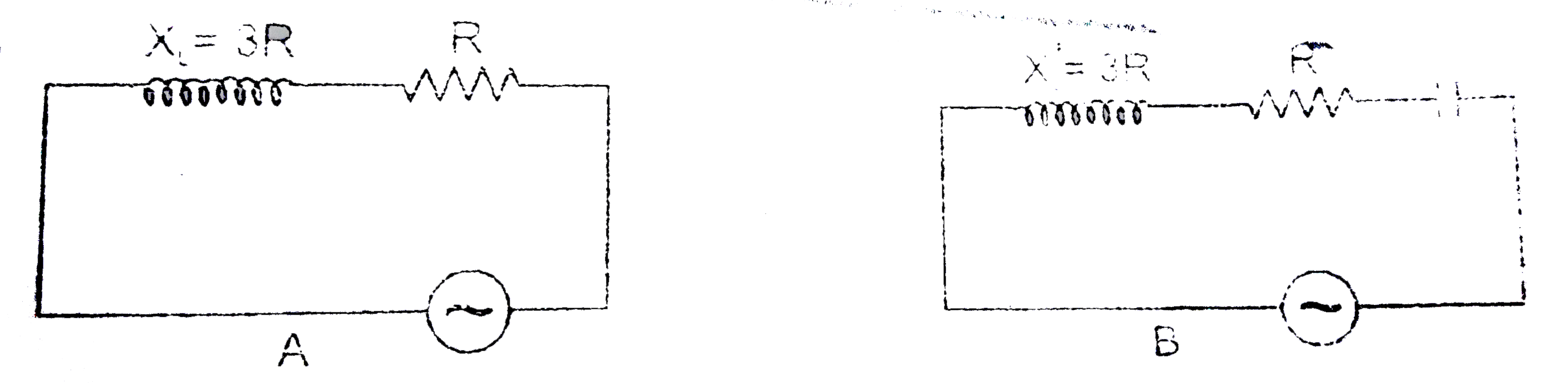
View SolutionIn the given circuit, power factor between A and B is 0.5 and over all power factor of the circuit is 1.
Find the value of Rand L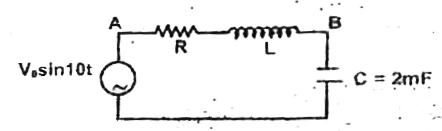
View SolutionIn the circuit shown there is a box and capacitance C connected to alternating power source of angular frequency of 2 rad//s. Box has power factor 1/√2 and circuit has overall power factor 1
1. Find the impedance of the box
View SolutionIn the circuit shown there is a box containing a resistor and an inductor and the box in series with the capacitance C connected to alternating power source of frequency to 2 rad/s. Box has power factor 1√2 and circuit has overall power factor 1. The impedance of the box is
View SolutionA 60 cycle AC, circuit has a resistance of 200Ω and inductor of 100 mH. What is the power factor? What capacitance placed in the circuit will make the power factor unity?
View SolutionIn a series LCR circuit, at resonance, power factor is …….. .
View SolutionIf V0 and I0 are the peak current and voltge across the resistor in a series L−C−R circuit, then the power dissipated in the circuit is (powerfac→r=cosθ)
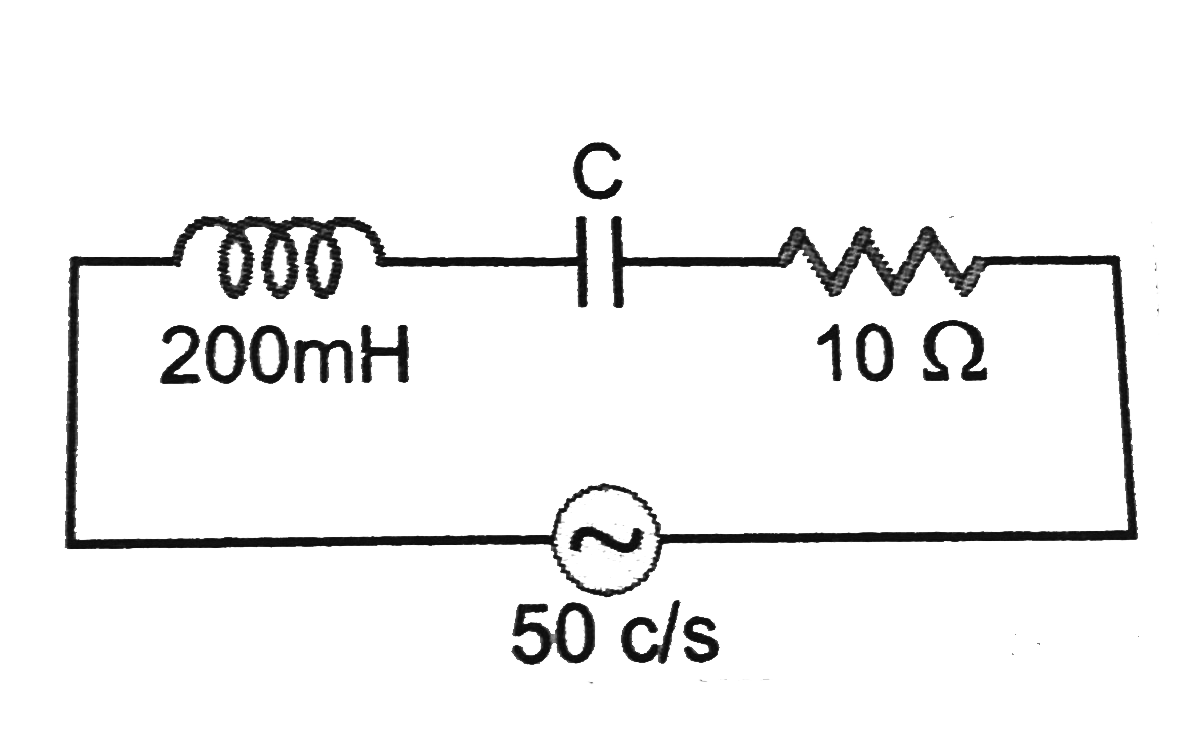
View SolutionIn the circuit shown in fin. Calculate the capacitance C of the capacitor, if the power factor of the circuit is unity. Also, calculate Q factor of the circuit.
View SolutionA series circuit has an impedance of 60.0Ω and a power factor of 0.720 at 50.0Hz. The source voltage lags the current.
(a) What circuit element, an inductor or a capacitor, should be placed in series with the circuit to raise its power factor?
(b) What size element will raise the power factor to unity?
View Solution
