When an alternating voltage of 220V is applied across a device P, a current of 0.25A flows through the circuit and it leads the applied voltage by a angle π2 radian. When the same voltage source is connected across another device Q, the same current is observed in the circuit but in phase with the applied voltage. What is the current when the same source is connected across a series combination of P and Q?
14√2 A lagging in phase by π4 with voltage
14√2 A leading in phase by π4 with voltage
1√2 A leading in phase by π4 with voltage
14√2 A leading in phase in π2 with voltage
The correct Answer is:B
To solve the problem, we need to analyze the two devices, P and Q, separately and then find the current when they are connected in series.
Step 1: Analyze Device P
When an alternating voltage of 220 V is applied across device P, a current of 0.25 A flows through the circuit, leading the applied voltage by an angle of π2 radians. This indicates that device P behaves like a capacitor.
Hint: Remember that in a purely capacitive circuit, the current leads the voltage by π2 radians.
Step 2: Calculate the Impedance of Device P
For device P, we can calculate the capacitive reactance XC using the formula:
XC=VrmsIrms=220V0.25A=880Ω
Hint: Use the formula for reactance to find the impedance in a capacitive circuit.
Step 3: Analyze Device Q
When the same voltage source is connected across device Q, the same current of 0.25 A is observed, but this time the current is in phase with the applied voltage. This indicates that device Q behaves like a resistor.
Hint: In a purely resistive circuit, the current is in phase with the voltage.
Step 4: Calculate the Resistance of Device Q
For device Q, we can calculate the resistance R using the same formula:
R=VrmsIrms=220V0.25A=880Ω
Hint: The resistance can be calculated in the same way as the reactance for device P.
Step 5: Calculate the Total Impedance in Series
When devices P and Q are connected in series, the total impedance Z is given by:
Z=√R2+X2C=√(880Ω)2+(880Ω)2=√2×(880)2=880√2Ω
Hint: Use the Pythagorean theorem to calculate the total impedance in a series circuit with resistive and reactive components.
Step 6: Calculate the Net Current in the Series Circuit
Now, we can find the net current Inet when the same voltage source is connected across the series combination of devices P and Q:
Inet=VrmsZ=220V880√2Ω=14√2A
Hint: Use Ohm's law to find the current in the series circuit.
Step 7: Determine the Phase Angle
To find the phase angle ϕ of the net current with respect to the applied voltage, we use:
cosϕ=RZ=880880√2=1√2
Thus, ϕ=π4 radians.
Hint: The phase angle can be found using the cosine of the ratio of resistance to total impedance.
Final Answer
The current when the same source is connected across a series combination of devices P and Q is:
Inet=14√2A
And the phase angle is π4 radians.
When an alternating voltage of 220 V is applied across device P, a current of 0.25 A flows through the circuit, leading the applied voltage by an angle of π2 radians. This indicates that device P behaves like a capacitor.
For device P, we can calculate the capacitive reactance XC using the formula:
XC=VrmsIrms=220V0.25A=880Ω
When the same voltage source is connected across device Q, the same current of 0.25 A is observed, but this time the current is in phase with the applied voltage. This indicates that device Q behaves like a resistor.
For device Q, we can calculate the resistance R using the same formula:
R=VrmsIrms=220V0.25A=880Ω
When devices P and Q are connected in series, the total impedance Z is given by:
Z=√R2+X2C=√(880Ω)2+(880Ω)2=√2×(880)2=880√2Ω
Now, we can find the net current Inet when the same voltage source is connected across the series combination of devices P and Q:
Inet=VrmsZ=220V880√2Ω=14√2A
To find the phase angle ϕ of the net current with respect to the applied voltage, we use:
cosϕ=RZ=880880√2=1√2
Thus, ϕ=π4 radians.
The current when the same source is connected across a series combination of devices P and Q is:
Inet=14√2A
And the phase angle is π4 radians.
Topper's Solved these Questions
- ALTERNATING CURRENTBOOK - DC PANDEY ENGLISHCHAPTER - ALTERNATING CURRENTEXERCISE - Level- 2More Than One Correct
8 Videos
- ALTERNATING CURRENTBOOK - DC PANDEY ENGLISHCHAPTER - ALTERNATING CURRENTEXERCISE - Level 2 Comprehension
6 Videos
- ALTERNATING CURRENTBOOK - DC PANDEY ENGLISHCHAPTER - ALTERNATING CURRENTEXERCISE - Level - 1 Subjective
6 Videos
- ATOMSBOOK - DC PANDEY ENGLISHCHAPTER - ATOMSEXERCISE - MEDICAL ENTRANCES GALLERY
42 Videos
Similar Questions
(a) Draw graphs showing the variations of inductive reactnace and capacitive reactance with frequency of the applied ac source .
(b) Draw the phasor diagram for a series RC circuit connected to an ac source.
(c ) An alternating voltage of 220 V is applied across a device X , a current of 0.25 A flows , which lag behind the applied voltage in phase by π2 radian . If the same voltage is applied across another device Y , the same current flows but now it is in phase with the applied voltage .
(i) Name the devices X and Y.
(ii) Calculate the current flowing in the circuit when the same voltage is applied across the series combination of X and Y.

View SolutionAn alternating voltage E=E0sinωt , is applied across a coil of inductor L. The current flowing through the circuit at any instant is
View Solution
Knowledge Check
When a voltage measuring device is connected to a.c. mains the meter shows the steady input voltage of 220V. This means
Ainput voltage cannot be ac voltage, but a dc voltage.Bmaximum input voltage is 220 VCthe meter reads voltage not V but <V2> and is calibrated to read √<V2>.Dthe pointer of the meter is stuck by some mechanical defect.
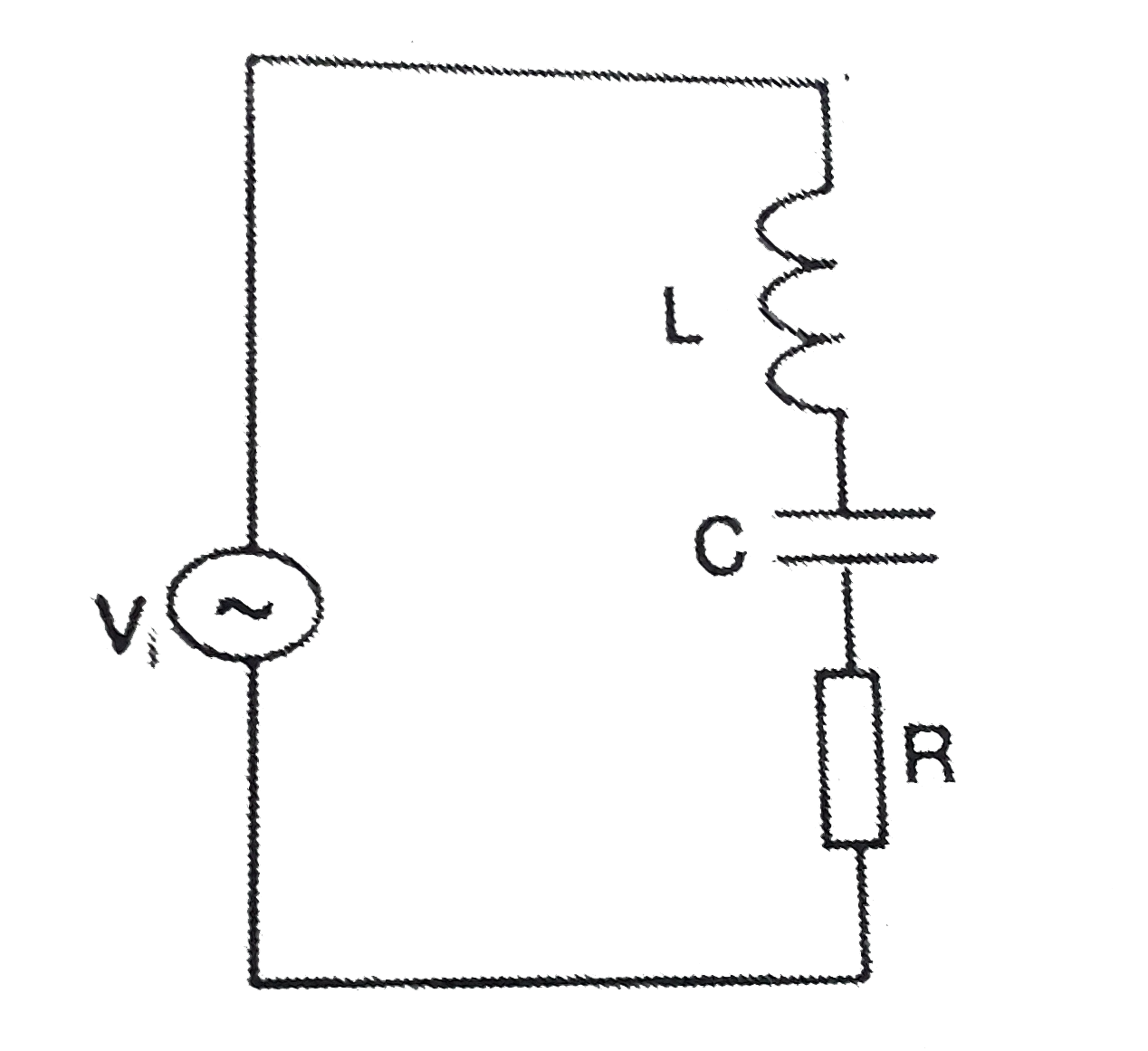
In the following circuit the current is in phase with the applied voltage. Therefore, the current in the circuit and the frequency of the source voltage respectively, are
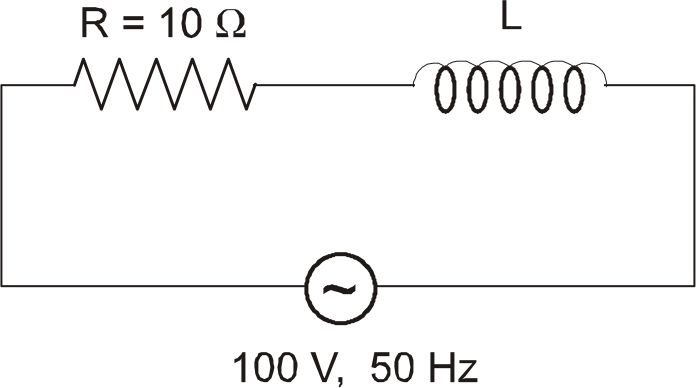
View SolutionWhen 100 V dc is applied across a coil, a current of 1A flows through it and when 100 V ac of 50 Hz is applied to the same coil, only 0.5 flows
The inductance of coil is
View SolutionIn LR circuit (shown in figure), current is lagging by π3 in phase with applied voltage, then select correct alternative:
View SolutionWhen a voltage measuring device is connected to a.c. mains the meter shows the steady input voltage of 220V. This means
View SolutionWhen a voltage measuring device is connected to a.c. mains the meter shows the steady input voltage of 220V. This means
View SolutionAn LCR circuit is connected to a source of alternating current. At resonance, the applied voltage and the current flowing through the circuit will have a phase difference of
View SolutionA 6 V, 12 W lamp is connected in series with a resistor R and a source of voltage 12 V.
What is the current flowing through the circuit?
View Solution
