If a 0.03 H inductor, a 10Ω resistor and a 2μF capacitor are connected in series. At what frequency will they resonate? What will be the phase angle at resonance?
To solve the problem step by step, we will follow these steps:
Step 1: Identify the given values
We have the following values:
- Inductance L=0.03H
- Resistance R=10Ω
- Capacitance C=2μF=2×10−6F
Step 2: Write the resonance condition
At resonance in an RLC circuit, the inductive reactance XL is equal to the capacitive reactance XC:
XL=XC
Where:
- XL=ωL
- XC=1ωC
Step 3: Set up the equation for resonance
Setting XL equal to XC:
ωL=1ωC
Step 4: Rearrange the equation
Multiplying both sides by ω:
ω2LC=1
Thus, we can express ω:
ω2=1LC
ω=1√LC
Step 5: Substitute the values of L and C
Substituting L and C into the equation:
ω=1√0.03×2×10−6
Step 6: Calculate ω
Calculating the value:
ω=1√0.03×2×10−6=1√6×10−8=1√6×104≈12.45×104≈4082.48rad/s
Step 7: Convert angular frequency to frequency
To find the frequency f, we use the relationship:
f=ω2π
Substituting the value of ω:
f=4082.482π≈4082.486.2832≈650Hz
Step 8: Calculate the phase angle at resonance
At resonance, the phase angle ϕ is given by:
cosϕ=RZ
Where Z (impedance) at resonance is equal to R:
Z=R
Thus:
cosϕ=RR=1
This implies:
ϕ=0∘
Final Answers
- Resonant frequency f≈650Hz
- Phase angle at resonance ϕ=0∘
---
We have the following values:
- Inductance L=0.03H
- Resistance R=10Ω
- Capacitance C=2μF=2×10−6F
At resonance in an RLC circuit, the inductive reactance XL is equal to the capacitive reactance XC:
XL=XC
Where:
- XL=ωL
- XC=1ωC
Setting XL equal to XC:
ωL=1ωC
Multiplying both sides by ω:
ω2LC=1
Thus, we can express ω:
ω2=1LC
ω=1√LC
Substituting L and C into the equation:
ω=1√0.03×2×10−6
Calculating the value:
ω=1√0.03×2×10−6=1√6×10−8=1√6×104≈12.45×104≈4082.48rad/s
To find the frequency f, we use the relationship:
f=ω2π
Substituting the value of ω:
f=4082.482π≈4082.486.2832≈650Hz
At resonance, the phase angle ϕ is given by:
cosϕ=RZ
Where Z (impedance) at resonance is equal to R:
Z=R
Thus:
cosϕ=RR=1
This implies:
ϕ=0∘
- Resonant frequency f≈650Hz
- Phase angle at resonance ϕ=0∘
Topper's Solved these Questions
- ALTERNATING CURRENTBOOK - DC PANDEY ENGLISHCHAPTER - ALTERNATING CURRENTEXERCISE - Level 1 Assertion-Reason
11 Videos
- ALTERNATING CURRENTBOOK - DC PANDEY ENGLISHCHAPTER - ALTERNATING CURRENTEXERCISE - Level - 1 Objective
30 Videos
- ALTERNATING CURRENTBOOK - DC PANDEY ENGLISHCHAPTER - ALTERNATING CURRENTEXERCISE - Exercise 28.1
3 Videos
- ATOMSBOOK - DC PANDEY ENGLISHCHAPTER - ATOMSEXERCISE - MEDICAL ENTRANCES GALLERY
42 Videos
Similar Questions
A 12 Ω resistor and a 0.21 H inductor are connected in series to an a.c. source operating at V, 50 cycle second. The phase angle between current and source vottage is
View SolutionA 12 Ω resistor and a 0.21 H inductor are connected in series to an a.c. source operating at V, 50 cycle second. The phase angle between current and source vottage is
View Solution
Knowledge Check
A 0.2kΩ resistor and 15μF capacitor are connected in series to a 220 V, 50 Hz ac source. The impadance of the circuit is
A250ΩB268ΩC29.15ΩD291.5Ω
Three resistors of 2Ω,3Ω and 4Ω are connected in
series
View SolutionA resistor R,an inductor L, and a capacitor C are connected in series to an oscillator of freqency υ.if the resonant frequency is υr, then the current lags behind voltage, when:
View SolutionAnswer the following:
(a) What do you understand by 'sharpness of resonance' for a series LCR resonant circuit? How is it related with the quality factor 'Q' of the circuit? Using the graphs given in the diagram, explain the factors which affect it. For which graph is the resistance (R ) minimum?
(b) A 2μF capacitor, 100Ω resistor and 8H inductor are connected in series with an ac source. Find the frequency of the ac source for which the current drawn in the circuit is maximum.
If the peak value of emf of the source is 200 V, calculate the (i) maximum current, and (ii) inductive and capacitive reactance of the circuit at resonance.
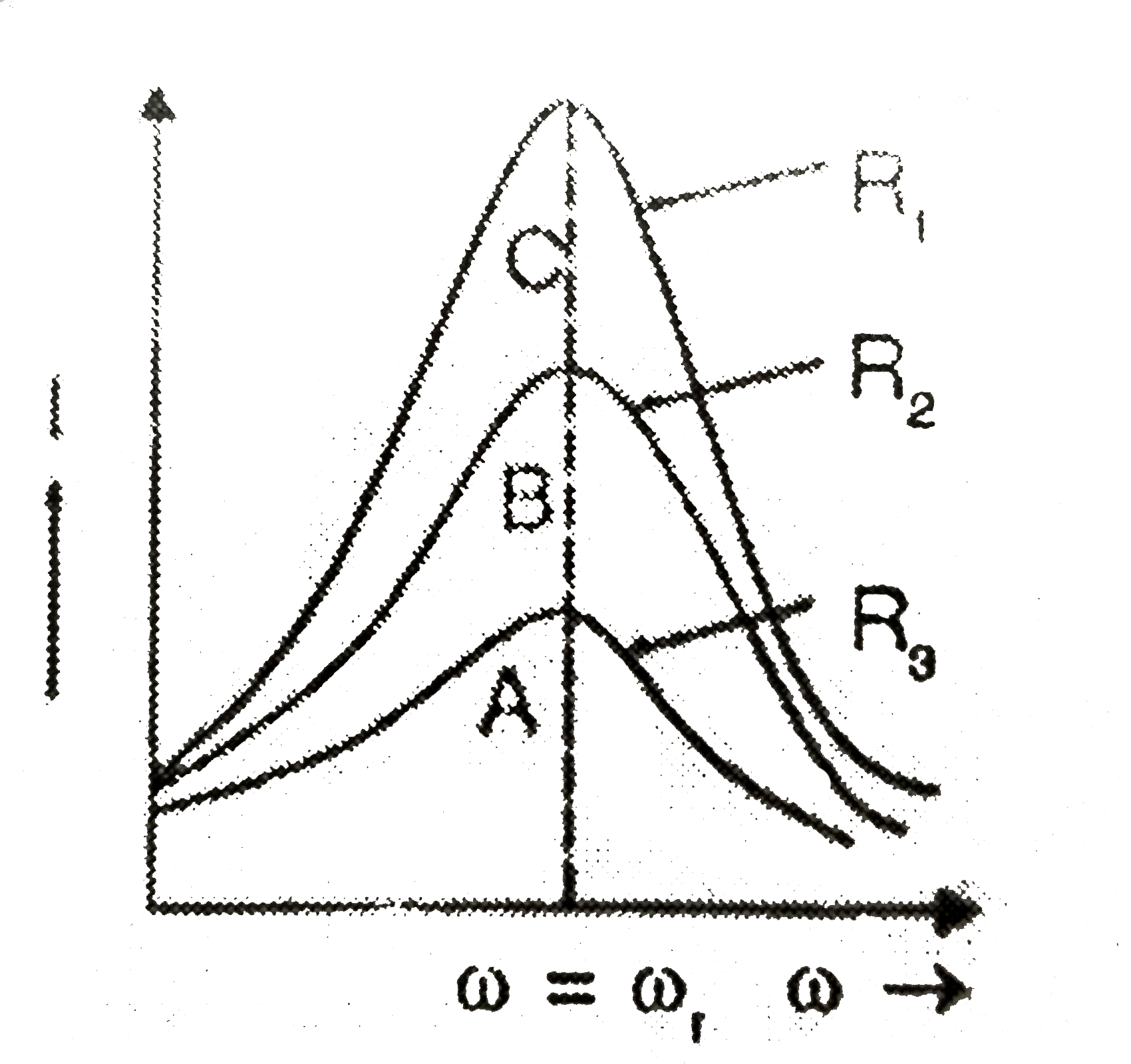
View SolutionA resistor R, an inductor L and a capacitor C are connected in series to an oscillator of frequency n. If the resonant frequency is nr, then the current lags behind voltage, when
View SolutionWhat is resonance ? What is resonant frequency ?
View SolutionA 0.21-H inductor and a 88−Ω resistor are connected in series to a 220-V, 50-Hz AC source. The current in the circuit and the phase angle between the current and the source voltage are respectively. (Useπ=22/7)
View SolutionA 0.21 H inductor and a 12Ω resistance are connected in series to a 220 V, 50 Hz ac source.
the phase angle between the current and the source voltage is
View Solution
