A metallic loop is placed in a non-uniform steady magnetic field. Will an emf be induced in the loop?
To determine whether an electromotive force (emf) is induced in a metallic loop placed in a non-uniform steady magnetic field, we can follow these steps:
Step 1: Understand the Concept of Magnetic Flux
Magnetic flux (Φ) through a surface is defined as the product of the magnetic field (B) and the area (A) through which it passes, taking into account the angle (θ) between the magnetic field lines and the normal to the surface. It is given by the formula:
Φ=B⋅A⋅cos(θ)
Step 2: Analyze the Magnetic Field
In this scenario, the magnetic field is described as non-uniform but steady. This means that while the strength of the magnetic field varies across different points in the loop, it does not change with time. For example, at different points in the loop, the magnetic field might be 3 Tesla at one point and 5 Tesla at another, but these values remain constant over time.
Step 3: Calculate the Total Magnetic Flux
To find the total magnetic flux through the loop, we would integrate the magnetic field over the area of the loop. However, since the magnetic field is steady (not changing with time), the total magnetic flux will also remain constant, even though its value may differ at various points in the loop.
Step 4: Apply Faraday's Law of Electromagnetic Induction
Faraday's law states that the induced emf (ε) in a closed loop is equal to the negative rate of change of magnetic flux through the loop:
ϵ=−dΦdt
Since the magnetic flux (Φ) is constant (as established in Step 3), the rate of change of flux (dΦ/dt) is zero.
Step 5: Conclude About the Induced EMF
Since the rate of change of magnetic flux is zero, we can conclude that:
ϵ=−dΦdt=0
Thus, no emf is induced in the loop.
Final Answer
No emf will be induced in the metallic loop placed in a non-uniform steady magnetic field.
---
Magnetic flux (Φ) through a surface is defined as the product of the magnetic field (B) and the area (A) through which it passes, taking into account the angle (θ) between the magnetic field lines and the normal to the surface. It is given by the formula:
Φ=B⋅A⋅cos(θ)
In this scenario, the magnetic field is described as non-uniform but steady. This means that while the strength of the magnetic field varies across different points in the loop, it does not change with time. For example, at different points in the loop, the magnetic field might be 3 Tesla at one point and 5 Tesla at another, but these values remain constant over time.
To find the total magnetic flux through the loop, we would integrate the magnetic field over the area of the loop. However, since the magnetic field is steady (not changing with time), the total magnetic flux will also remain constant, even though its value may differ at various points in the loop.
Faraday's law states that the induced emf (ε) in a closed loop is equal to the negative rate of change of magnetic flux through the loop:
ϵ=−dΦdt
Since the magnetic flux (Φ) is constant (as established in Step 3), the rate of change of flux (dΦ/dt) is zero.
Since the rate of change of magnetic flux is zero, we can conclude that:
ϵ=−dΦdt=0
Thus, no emf is induced in the loop.
No emf will be induced in the metallic loop placed in a non-uniform steady magnetic field.
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTIONBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Exercise 27.2
4 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Exercise 27.3
4 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Miscellaneous Examples
5 Videos
- CURRENT ELECTRICITYBOOK - DC PANDEY ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - Medical entrances gallery
97 Videos
- ELECTROMAGNETIC WAVESBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - Sec C
22 Videos
Similar Questions
Knowledge Check
A conducting circular loop is placed in a uniform magnetic field, B=0.025T with its plane perpendicular to the loop. The radius of the loop is made to shrink at a constant rate of 1mms−1. The induced emf when the radius is 2cm is
A2πμVBπμVCπ2μVD2μV
A coil of metal wire is kept stationary in a non-uniform magnetic field. An e.m.f. Is induced in the coil.
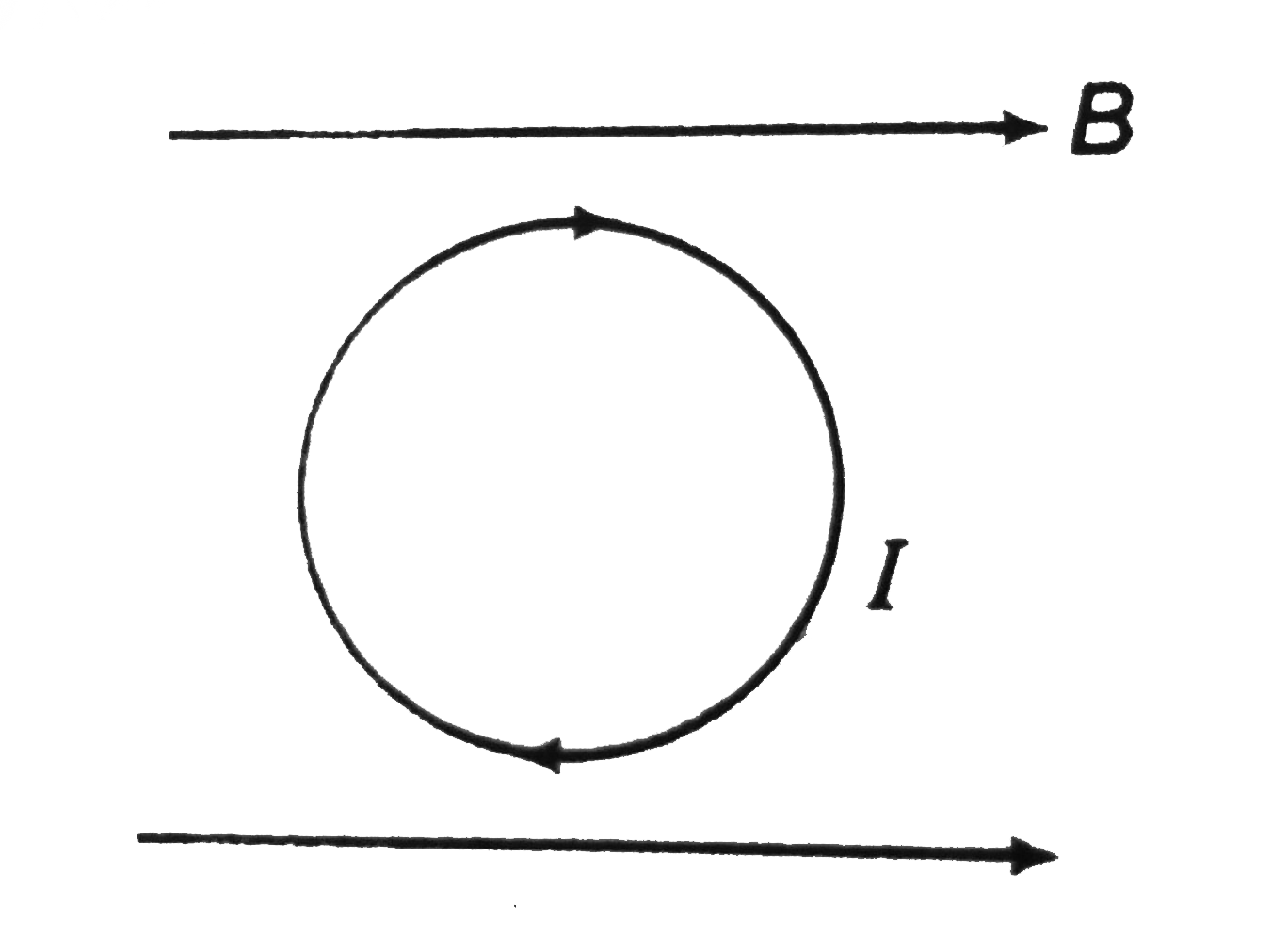
View SolutionAssertion : A current carrying loop is placed in uniform magnetic field as shown in figure. Torque in the loop in this case is zero.
Reason : Magnetic moment vector of the loop is perpendicular to paper inwards.
View SolutionA: When a conducting loop is kept stationary in a non-uniform magnetic field an emf is induced.
R: As per Faraday's law, whenever flux changes, an emf is induced.
View SolutionA current carrying loop is placed in the non-uniform magnetic field whose variation in space is shown in fig. Direction of magnetic field is into the plane of paper. The magnetic force experienced by the loop is
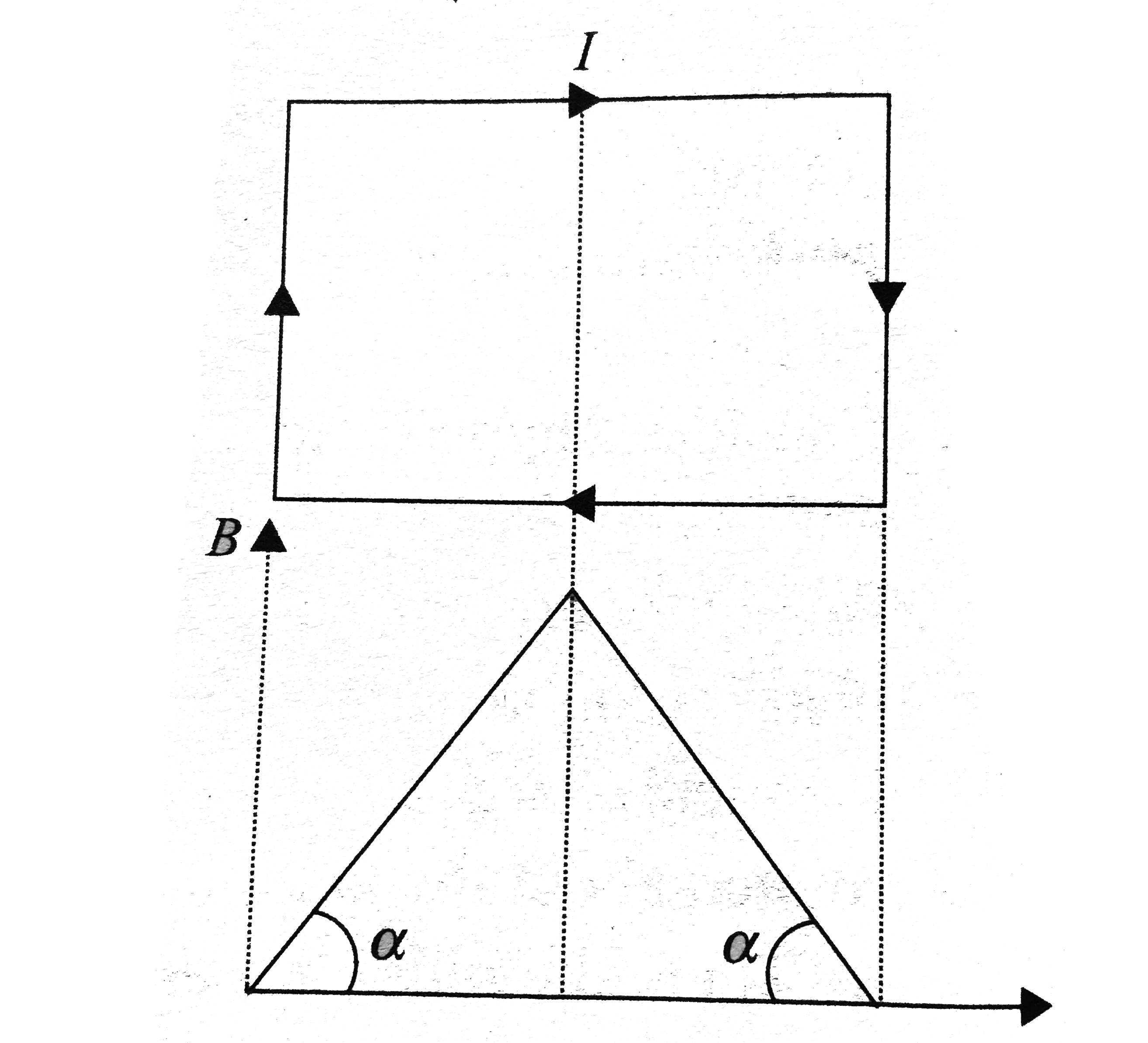
View SolutionAssertion If a loop is placed in a non-uniform (with respect to position) magnetic field, then induced emf is produced in the loop.
Reason In a non-uniform magnetic field, magnetic flux passing through the loop will change. Therefore, induced emf is produced.
View SolutionA metallic loop is placed in a magnetic field. If a current is passed through it, then
View SolutionA semi circular current loop is placed in an uniform magnetic field of 1 tesla as shown. If the radius of loop is 1 m, the magnetic force on the loop is
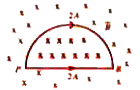
View Solution