An air capacitor is first charged through a battery. The charging battery is then removed and a electric slab of dielectric constant K=4 is inserted between the plates. Simultaneously, the distance between the plates is reduced to half, then find change, C,E,V and U.
To solve the problem step by step, we need to analyze the changes in capacitance (C), electric field (E), potential difference (V), and stored energy (U) when a dielectric slab is inserted into a charged capacitor and the distance between the plates is halved.
Step 1: Initial Parameters
Let:
- Initial capacitance C0=ϵ0Ad
- Initial electric field E0=V0d
- Initial potential difference V0
- Charge Q on the capacitor after charging through the battery.
Step 2: Inserting the Dielectric
When a dielectric slab with dielectric constant K=4 is inserted, the new capacitance C′ can be calculated using the formula:
C′=K⋅C0=4⋅C0
Step 3: Reducing the Distance
The distance between the plates is reduced to half, so the new distance d′ is:
d′=d2
The new capacitance can be expressed as:
C′=K⋅ϵ0Ad′=4⋅ϵ0Ad2=8⋅ϵ0Ad=8⋅C0
Step 4: Electric Field Calculation
The electric field E′ after inserting the dielectric and reducing the distance is given by:
E′=V′d′
Since the charge Q remains constant (battery is removed), the new potential difference V′ can be calculated using:
V′=QC′=Q8C0
Thus, the new electric field becomes:
E′=V′d′=Q8C0d2=Q8C0⋅2d=Q4C0d=E04
Step 5: Potential Difference Calculation
From the above, we find:
V′=QC′=Q8C0=V08
Step 6: Energy Calculation
The stored energy U′ in the capacitor is given by:
U′=Q22C′=Q22⋅8C0=Q216C0=U08
where U0=Q22C0 is the initial energy.
Summary of Changes
- New Capacitance C′=8C0
- New Electric Field E′=E04
- New Potential Difference V′=V08
- New Stored Energy U′=U08
Let:
- Initial capacitance C0=ϵ0Ad
- Initial electric field E0=V0d
- Initial potential difference V0
- Charge Q on the capacitor after charging through the battery.
When a dielectric slab with dielectric constant K=4 is inserted, the new capacitance C′ can be calculated using the formula:
C′=K⋅C0=4⋅C0
The distance between the plates is reduced to half, so the new distance d′ is:
d′=d2
The new capacitance can be expressed as:
C′=K⋅ϵ0Ad′=4⋅ϵ0Ad2=8⋅ϵ0Ad=8⋅C0
The electric field E′ after inserting the dielectric and reducing the distance is given by:
E′=V′d′
Since the charge Q remains constant (battery is removed), the new potential difference V′ can be calculated using:
V′=QC′=Q8C0
Thus, the new electric field becomes:
E′=V′d′=Q8C0d2=Q8C0⋅2d=Q4C0d=E04
From the above, we find:
V′=QC′=Q8C0=V08
The stored energy U′ in the capacitor is given by:
U′=Q22C′=Q22⋅8C0=Q216C0=U08
where U0=Q22C0 is the initial energy.
- New Capacitance C′=8C0
- New Electric Field E′=E04
- New Potential Difference V′=V08
- New Stored Energy U′=U08
Topper's Solved these Questions
- CAPACITORSBOOK - DC PANDEY ENGLISHCHAPTER - CAPACITORSEXERCISE - Exercise
155 Videos
- CAPACITORSBOOK - DC PANDEY ENGLISHCHAPTER - CAPACITORSEXERCISE - OBJECTIVE_TYPE
1 Videos
- ATOMSBOOK - DC PANDEY ENGLISHCHAPTER - ATOMSEXERCISE - MEDICAL ENTRANCES GALLERY
42 Videos
- COMMUNICATION SYSTEMBOOK - DC PANDEY ENGLISHCHAPTER - COMMUNICATION SYSTEMEXERCISE - Subjective
11 Videos
Similar Questions
A parallel plate capacitor is charged by a battery. After some time the battery is disconnected and a dielectric slab of dielectric constant K is inserted between the plates. How would (i) the capacitance, (ii) the electric field between the plates and (iii) the energy stored in the capacitor, be affected ? Justify your answer.
View SolutionAn air-cored parallel plate capacitor having a capacitance C is charged by connecting it to a battery. Now, it is disconnected from the battery and a dielectric slab of dielectric constant K is inserted between its plates so as to completely fill the space between the plates. Compare :
(I) Initial and final capacitance
(ii) Initial and final charge.
(iii) Initial and final potential difference.
(iv) Initial an final electric field between the plates.
(v) Initial and final energy stored in the capacitor.
View SolutionAir filled capacitor is charged by a battery and after charging battery is removed. A slab of dielectric material is inserted in it to fill the space completely . The electric field in the capacitor is
View SolutionA parallel plate capacitor (without dielectric) is charged by a battery and kept connected to the battery. A dielectric salb of dielectric constant 'k' is inserted between the plates fully occupying the space between the plates. The energy density of electric field between the plates will:
View SolutionA parallel capacitor of capacitance C is charged and disconnected from the battery. The energy stored in it is E. If a dielectric slab of dielectric constant 6 is inserted between the plates of the capacitor then energy and capacitance will become.
View SolutionA capacitor is connected to a battery of voltage V. Now a di-electric slab of di-electric constant k is completely inserted between the plates, then the final charge on the capacitor will be : (If initial charge is q0)
View SolutionThe potential enery of a charged parallel plate capacitor is U0. If a slab of dielectric constant K is inserted between the plates, then the new potential energy will be
View SolutionThe potential enery of a charged parallel plate capacitor is U0. If a slab of dielectric constant K is inserted between the plates, then the new potential energy will be
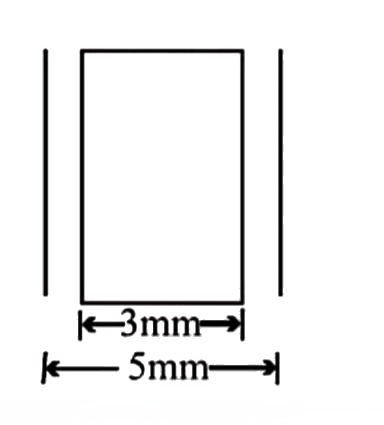
View SolutionSeparation between the plates of parallel plate capacitor is 5 mm. this capacitor, having air as the dielectric medium between the plates, is charged to a potential difference 25 V using a battery. The battery is then disconnected and a dielectric slab of thickness 3mm and dielectric constant K=10 is placed between the plates as shown. potential difference between the plates after the dielectric slab has been introduced is-
View SolutionAn uncharged parallel plate capacitor is connected to a battery. The electric field between the plates is 10V/m. Now a dielectric of dielectric constant 2 is inserted between the plates filling the entries space. The electric field between the plates now is
View Solution
