Question

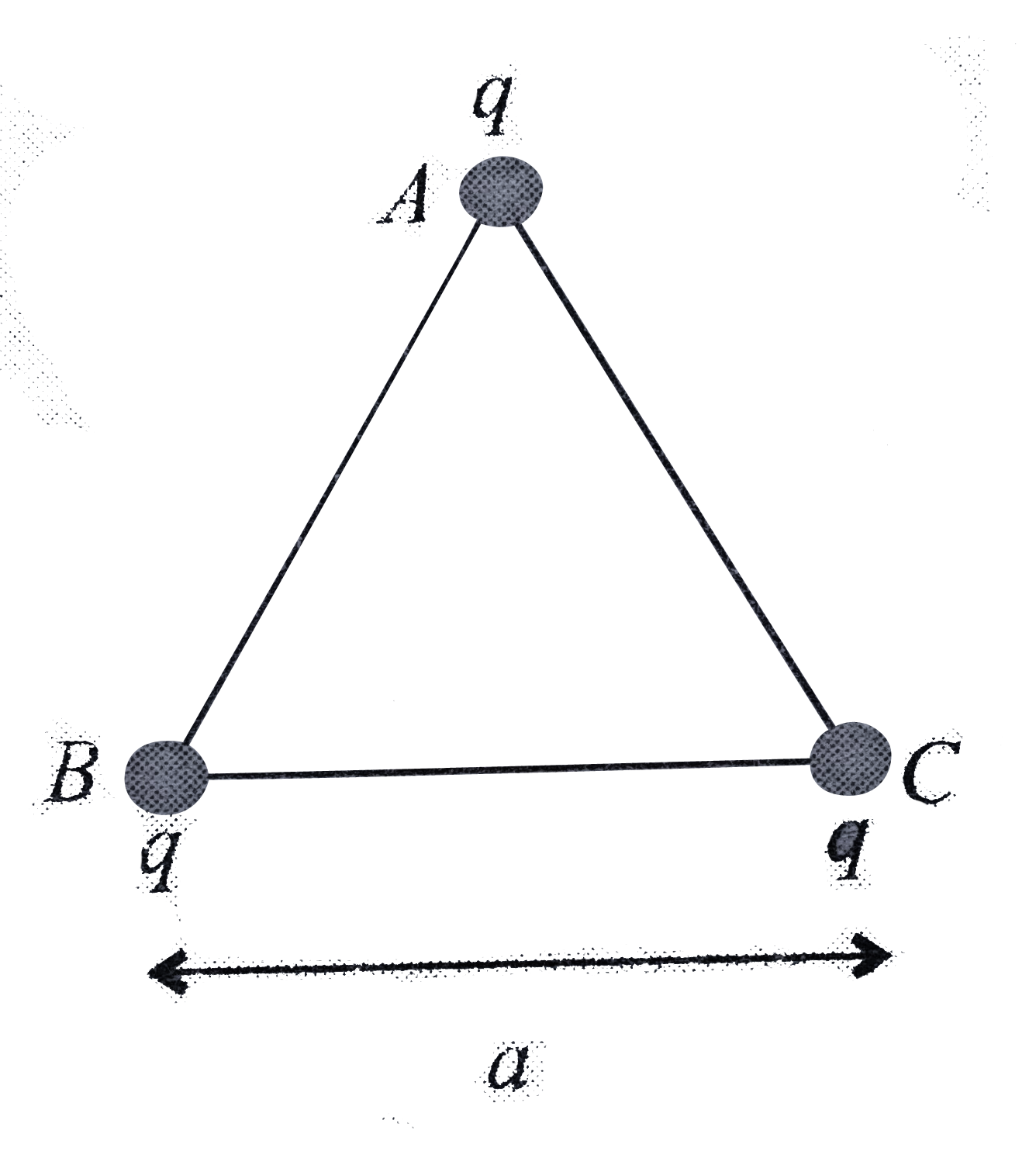
Two identical charges are placed at the two corners of an equilateral triangle. The potential energy of the system is U. The work done in bringing an identical charge from infinity to the third vertex is

Options

A. `U`
B. `2U`
C. `3U`
D. `4U`

Answer

B

Explanation

To solve the problem step by step, we will analyze the situation involving the potential energy of the system of charges.

Step 1: Understand the Configuration
We have two identical charges, let's say each charge is \( Q \), placed at two corners of an equilateral triangle. The distance between these two charges is \( a \).

Step 2: Calculate Initial Potential Energy
The potential energy \( U \) of the system with just the two charges at points A and B can be calculated using the formula for the potential energy between two point charges:
\( U = \frac{k Q^2}{a} \)
where \( k \) is Coulomb's constant.

Step 3: Bringing the Third Charge
Now, we want to bring a third identical charge \( Q \) from infinity to the third vertex \( C \) of the triangle.

Step 4: Calculate Final Potential Energy
When the third charge is brought to vertex \( C \), we need to consider the potential energy contributions from all pairs of charges:
1. Between charge at A and C:
\( U_{AC} = \frac{k Q^2}{a} \)
2. Between charge at B and C:
\( U_{BC} = \frac{k Q^2}{a} \)
3. Between charges at A and B (already calculated):
\( U_{AB} = \frac{k Q^2}{a} \)

Now, the total final potential energy \( U_f \) of the system when the third charge is at C is:
\( U_f = U_{AB} + U_{AC} + U_{BC} = \frac{k Q^2}{a} + \frac{k Q^2}{a} + \frac{k Q^2}{a} = 3 \cdot \frac{k Q^2}{a} = 3U \)

Step 5: Calculate Work Done
The work done \( W \) in bringing the charge from infinity to point C is equal to the change in potential energy of the system:
\( W = U_f - U = 3U - U = 2U \)

Final Answer
Thus, the work done in bringing the identical charge from infinity to the third vertex is:
\( W = 2U \)

---