At a far away distance r along the axis from a electric dipole electric field is E. Find the electric field at distance 2r along the perpendicular bisector.
The correct Answer is:A
To find the electric field at a distance 2r along the perpendicular bisector of an electric dipole, we can follow these steps:
1. Understanding the Electric Field of a Dipole:
The electric field E at a distance r along the axis of a dipole is given by the formula:
E=2kpr3
where k is the Coulomb's constant and p is the dipole moment.
2. Identifying the Point of Interest:
We need to find the electric field at a point Q located at a distance 2r along the perpendicular bisector of the dipole.
3. Using the Formula for the Perpendicular Bisector:
The electric field EQ at a distance r along the perpendicular bisector of a dipole is given by:
EQ=kpr3
For our case, since we are at a distance 2r, we can substitute r with 2r in the formula:
EQ=kp(2r)3
4. Calculating the Electric Field:
Simplifying the expression, we have:
EQ=kp8r3
5. Relating to the Given Electric Field E:
From the earlier step, we know that:
E=2kpr3
To relate EQ to E, we can express kp in terms of E:
kp=Er32
Substituting this into the expression for EQ:
EQ=Er328r3=E16
6. Final Result:
Thus, the electric field at a distance 2r along the perpendicular bisector is:
EQ=E16
The electric field E at a distance r along the axis of a dipole is given by the formula:
E=2kpr3
where k is the Coulomb's constant and p is the dipole moment.
We need to find the electric field at a point Q located at a distance 2r along the perpendicular bisector of the dipole.
The electric field EQ at a distance r along the perpendicular bisector of a dipole is given by:
EQ=kpr3
For our case, since we are at a distance 2r, we can substitute r with 2r in the formula:
EQ=kp(2r)3
Simplifying the expression, we have:
EQ=kp8r3
From the earlier step, we know that:
E=2kpr3
To relate EQ to E, we can express kp in terms of E:
kp=Er32
Substituting this into the expression for EQ:
EQ=Er328r3=E16
Thus, the electric field at a distance 2r along the perpendicular bisector is:
EQ=E16
Topper's Solved these Questions
- ELECTROSTATICSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Example Type 6
4 Videos
- ELECTROSTATICSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Example Type 8
3 Videos
- ELECTROSTATICSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Medical entrances gallery
37 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITORSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITORSEXERCISE - (C) Chapter exercises
50 Videos
- GRAVITATIONBOOK - DC PANDEY ENGLISHCHAPTER - GRAVITATIONEXERCISE - All Questions
135 Videos
Similar Questions
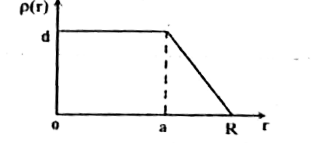
The electric field at r= R is
View SolutionAn electric dipole placed in a nonuniform electric field experience
View SolutionElectric field on the axis of a small electric dipole at a distance r is →E1 and →E2 at a distance of 2r on a line of perpendicular bisector is
View SolutionAn electric dipole is placed in a uniform electric field. The net electric force on the dipole
View SolutionTwo particles A and B, having opposite charges2.0×10−6 and −2.0×10−6C , are placed at a separaton of 1.0 cm.(a) write down the electric dipole moment (b) Calculate the electric field at a point on the axis of the dipole 1.0 m away from the centre. (c ) Calculate the electric field at a point on the perpendicular bisector of the dipole and 1.0 m away from the centre.
View SolutionThe electric field due to a short dipole at a distance r, on the axial line, from its mid point is the same as electric field at a distance r′ on the equatorial line, from its mid point.Determine the ratio r/r'.
View SolutionA charge q is uniformly distributed along an insulating straight wire of length 2l as shown in Fig. Find an expression for the electric potential at a point located a distance d from the distribution along its perpendicular bisector.
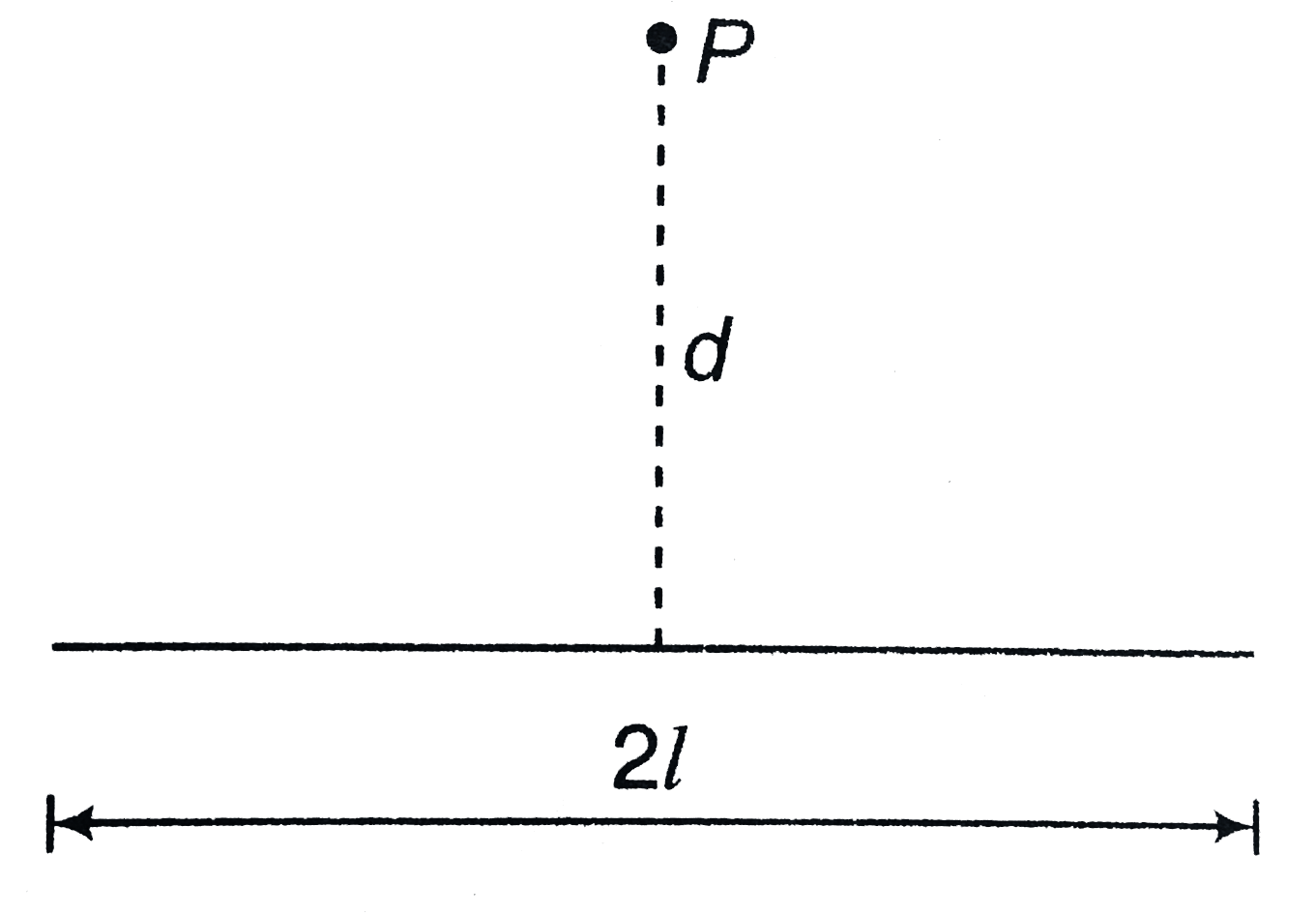
View SolutionDue to an electric dipole shown in fig., the electric field intensity is parallel to dipole axis :

View SolutionThe figure shows electric field lines. If EA and EB are electric fields at A and B and distance AB is r, then

View SolutionThe electric field at a distance 3R/2 from the centre of a charge conducting spherical shell of radius R is E. The electric field at a distance R/2 from the centre of the sphere is
View Solution
