A conductor has a temperature independent resistance R and a total heat capacity C. At the moment t=0 it is connected to a DC voltage V. Find the times dependence of the conductors temperature t assuming the thermal power dissipated into surrounding space to vary as q=k(T−T0) where k is a constant T0 is the surrounding temperature (equal to conductor's temperature at the initial moment).
The correct Answer is:A, B, C
To find the time dependence of the conductor's temperature T(t) when a DC voltage V is applied, we can follow these steps:
Step 1: Understand the Heat Generation and Loss
The power P generated in the conductor due to the applied voltage is given by:
P=V2R
This power will increase the temperature of the conductor. However, the conductor also loses heat to the surroundings. The rate of heat loss Q is given by:
Q=k(T−T0)
where T0 is the surrounding temperature.
Step 2: Set Up the Heat Balance Equation
The change in heat energy dQ in the conductor can be expressed using its heat capacity C:
dQ=CdTdt
The net heat change in the conductor can be described by the equation:
V2R−k(T−T0)=CdTdt
Step 3: Rearrange the Equation
Rearranging the equation gives:
CdTdt+k(T−T0)=V2R
This can be rewritten as:
dTdt+kC(T−T0)=V2RC
Step 4: Solve the Differential Equation
This is a first-order linear differential equation. To solve it, we can use an integrating factor. The integrating factor μ(t) is given by:
μ(t)=e∫kCdt=ektC
Multiplying through by the integrating factor:
ektCdTdt+kCektC(T−T0)=V2RCektC
Step 5: Integrate Both Sides
Integrating both sides with respect to t:
ddt(TektC)=V2RCektC+kT0CektC
Integrating gives:
TektC=∫(V2RC+kT0C)ektCdt+C1
Step 6: Solve for T
After integrating, we can express T:
T(t)=T0+V2kR(1−e−ktC)
Final Expression
Thus, the time dependence of the conductor's temperature is:
T(t)=T0+V2kR(1−e−ktC)
The power P generated in the conductor due to the applied voltage is given by:
P=V2R
This power will increase the temperature of the conductor. However, the conductor also loses heat to the surroundings. The rate of heat loss Q is given by:
Q=k(T−T0)
where T0 is the surrounding temperature.
The change in heat energy dQ in the conductor can be expressed using its heat capacity C:
dQ=CdTdt
The net heat change in the conductor can be described by the equation:
V2R−k(T−T0)=CdTdt
Rearranging the equation gives:
CdTdt+k(T−T0)=V2R
This can be rewritten as:
dTdt+kC(T−T0)=V2RC
This is a first-order linear differential equation. To solve it, we can use an integrating factor. The integrating factor μ(t) is given by:
μ(t)=e∫kCdt=ektC
Multiplying through by the integrating factor:
ektCdTdt+kCektC(T−T0)=V2RCektC
Integrating both sides with respect to t:
ddt(TektC)=V2RCektC+kT0CektC
Integrating gives:
TektC=∫(V2RC+kT0C)ektCdt+C1
After integrating, we can express T:
T(t)=T0+V2kR(1−e−ktC)
Thus, the time dependence of the conductor's temperature is:
T(t)=T0+V2kR(1−e−ktC)
Topper's Solved these Questions
- CURRENT ELECTRICITYBOOK - DC PANDEY ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - Example
65 Videos
- CURRENT ELECTRICITYBOOK - DC PANDEY ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - Check point
70 Videos
- CURRENT ELECTRICITYBOOK - DC PANDEY ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - Level 2 Comprehension Example Type
2 Videos
- COMMUNICATION SYSTEMBOOK - DC PANDEY ENGLISHCHAPTER - COMMUNICATION SYSTEMEXERCISE - Subjective
11 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Medical entrances gallery
25 Videos
Similar Questions

Two ends of a rod of uniform cross sectional area are kept at temperature 3T0 and T0 as shown. Thermal conductivity of rod varies as k=αT, (where α is a constant and T is absolute temperature). In steady state, the temperature of the middle section of the rod is
View SolutionFind the relatio between volume and temperature of a gas in a process, in which the molar heat capacity C varies with temperature T as C=CV+αT. [α is a constant] .
View SolutionThe temperature T of a cooling object drops at a rate proportional to the difference T−S where S is constant temperature of surrounding medium. If initially T=150∘C; find the temperature of the cooling object at any time t.
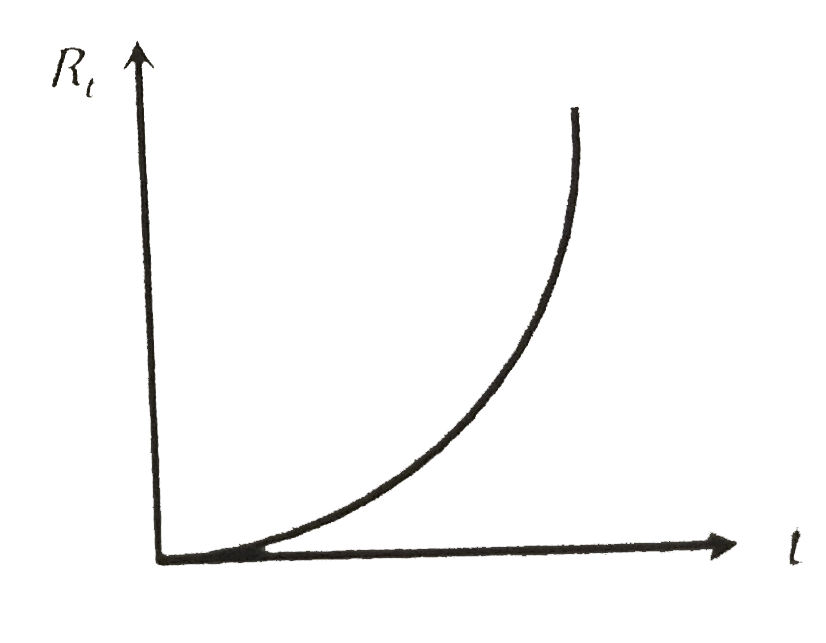
View SolutionThe resistance R of a conductor varies with temperature t as shown in the figure. If the variation is represented by Rt=R0[1+αt+βt2], then
View SolutionThe specific heat of many solids at low temperatures varies with absolute temperature T according to the relation S=AT3, where A is a constant. The heat energy required to raise the temperature of a mass m of such a solid from T = 0 to T = 20 K is
View SolutionThe specific heat of a metal at low temperatures varies according to S=aT3, where a is a constant and T is absolute temperature. The heat energy needed to raise unit mass of the metal from temperature T=1K to T=2K is
View SolutionThe co-efficient of thermal expansion of a rod is temperature dependent and is given by the formula α=aT, where a is a positive constant at T in∘C. if the length of the rod is l at temperature 0∘C, then the temperature at which the length will be 2l is
View SolutionThe temperature coefficient of resistance of conductor varies as α(T)=3T2+2T. If R0 is resistance at T = 0and R is resistance at T, then
View SolutionThe rate of dissipation of heat by a black body at temperature T is Q. What will be the the rate of dissipation of heat by another body at temperature 2T and emissivity 0.25?
View SolutionIf a piece of metal is heated to temperature θ and the allowed to cool in a room which is at temperature θ0, the graph between the temperature T of the metal and time t will be closet to
View Solution
