Two conducting rods when connected between two points at constant but different temperatures separately, the rate of heat flow through them is q1andq2.
When they are connected in series, the net rate of heat flow is q1+q2
When they are connected in series, the net rate of heat flow is (q1q2q1+q2)
When they are connected in parallel, the net rate of heat flow is q1+q2
When they are connected in parallel, the net rate of heat flow is (q1q2q1+q2)
The correct Answer is:B, C
To solve the problem regarding the rate of heat flow through two conducting rods connected at constant but different temperatures, we will analyze the situation in both series and parallel configurations.
1. Identify the Given Variables:
- Let q1 be the rate of heat flow through the first rod.
- Let q2 be the rate of heat flow through the second rod.
- Let R1 be the resistance of the first rod.
- Let R2 be the resistance of the second rod.
- Let θ be the temperature difference across the rods.
2. Use the Formula for Heat Flow:
The rate of heat flow through a conductor is given by the formula:
q=θR
Therefore, for the first rod:
q1=θR1
And for the second rod:
q2=θR2
3. Case 1: Rods Connected in Series:
- When the rods are connected in series, the effective resistance Reff is:
Reff=R1+R2
- The total heat flow qseries through the series connection is:
qseries=θReff=θR1+R2
- Using the expressions for q1 and q2, we can express this as:
qseries=q1q2q1+q2
4. Case 2: Rods Connected in Parallel:
- When the rods are connected in parallel, the effective resistance Reff is:
1Reff=1R1+1R2
- This can be rewritten as:
Reff=R1R2R1+R2
- The total heat flow qparallel through the parallel connection is:
qparallel=θReff=θ(R1+R2)R1R2
- Again, using the expressions for q1 and q2, we can express this as:
qparallel=q1+q2
5. Conclusion:
- For the series connection, the heat flow is given by:
qseries=q1q2q1+q2
- For the parallel connection, the heat flow is given by:
qparallel=q1+q2
Final Answer:
- The correct expressions for heat flow are:
- In series: qseries=q1q2q1+q2
- In parallel: qparallel=q1+q2
- Let q1 be the rate of heat flow through the first rod.
- Let q2 be the rate of heat flow through the second rod.
- Let R1 be the resistance of the first rod.
- Let R2 be the resistance of the second rod.
- Let θ be the temperature difference across the rods.
The rate of heat flow through a conductor is given by the formula:
q=θR
Therefore, for the first rod:
q1=θR1
And for the second rod:
q2=θR2
- When the rods are connected in series, the effective resistance Reff is:
Reff=R1+R2
- The total heat flow qseries through the series connection is:
qseries=θReff=θR1+R2
- Using the expressions for q1 and q2, we can express this as:
qseries=q1q2q1+q2
- When the rods are connected in parallel, the effective resistance Reff is:
1Reff=1R1+1R2
- This can be rewritten as:
Reff=R1R2R1+R2
- The total heat flow qparallel through the parallel connection is:
qparallel=θReff=θ(R1+R2)R1R2
- Again, using the expressions for q1 and q2, we can express this as:
qparallel=q1+q2
- For the series connection, the heat flow is given by:
qseries=q1q2q1+q2
- For the parallel connection, the heat flow is given by:
qparallel=q1+q2
- The correct expressions for heat flow are:
- In series: qseries=q1q2q1+q2
- In parallel: qparallel=q1+q2
Topper's Solved these Questions
- CALORIMETRY & HEAT TRANSFERBook:DC PANDEY ENGLISHChapter:CALORIMETRY & HEAT TRANSFERExercise:Level 2 Subjective
Explore 14 Videos
- CALORIMETRY & HEAT TRANSFERBook:DC PANDEY ENGLISHChapter:CALORIMETRY & HEAT TRANSFERExercise:Level 2 Single Correct
Explore 7 Videos
- BASIC MATHEMATICSBook:DC PANDEY ENGLISHChapter:BASIC MATHEMATICSExercise:Exercise
Explore 13 Videos
- CALORIMETRY AND HEAT TRANSFERBook:DC PANDEY ENGLISHChapter:CALORIMETRY AND HEAT TRANSFERExercise:Medical entrance s gallery
Explore 38 Videos
Similar Questions
heat flows between two bodies due to difference in their
View SolutionA and B are two points on uniform metal ring whose centre is O The angle AOB=θ A and B are maintaind at two different constant temperatures When θ=180∘ the rate of total heat flow from A to B is 1.2W When θ=90∘ this rate will be .
View Solution
Knowledge Check
Heat is flowing through two cylindrical rods of the same material. The diamters of the rods are in the ratio 1:2 and the length in the ratio 2:1. If the temperature difference between the ends is same then ratio of the rate of flow of heat through them will be
A1:1B1:8C2:1D8:1
A copper rod and a steel rod of equal cross -sections and lengths (L) are joined side by side and connected between two heat baths as shown in the figure. If heat flows through them from x=0 to x=2L at a steady rate, and conductivities of the metals are Kcu & Ksteel(Kcu>Ksteel), then the temperature varies with x as (convention and radiation are negligible)
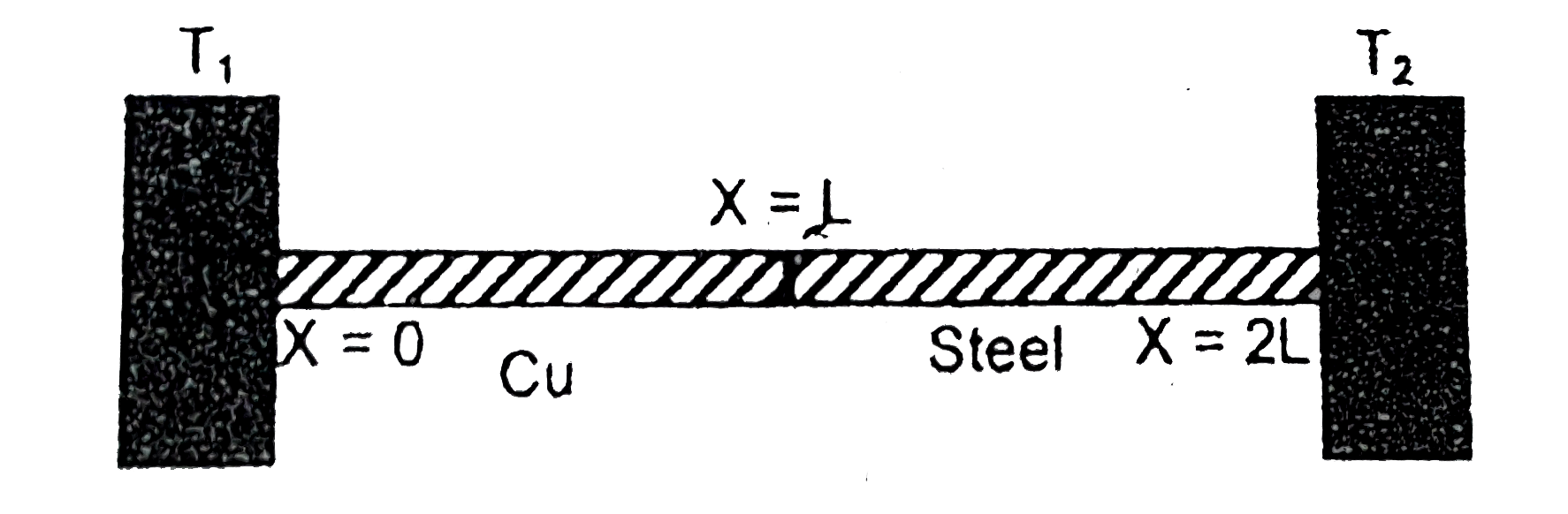
View Solution
Three rods of same dimensions are arranged as shown in Fig. They have thermal conductivities K1,K2 and K3. The points P and Q are maintained at different temeperature for the heat to flow at the same rate along PRQ and PQ. Whi of the following options correct?
View SolutionTwo conducting spheres of radius R and 3R carry charges Q and −2Q. Between these spheres a neutral conducting sphere of radius 2R is connected. The separation between the sphere is considerably large Charge flows through conducting wire due to potential difference.

The final charge on initially neutral conducting sphere is :
View SolutionTwo conducting spheres of radius R and 3R carry charges Q and −2Q. Between these spheres a neutral conducting sphere of radius 2R is connected. The separation between the sphere is considerably large Charge flows through conducting wire due to potential difference.

The decrease in electric potential energy of sphere of radius R is :
View SolutionTwo conducting spheres of radius R and 3R carry charges Q and −2Q. Between these spheres a neutral conducting sphere of radius 2R is connected. The separation between the sphere is considerably large Charge flows through conducting wire due to potential difference.

The final electric potential of sphere of radius 3R will be :
View SolutionFive rods of same dimensions are arranged as shown in the figure. They have thermal conductivities K1,K2,K3,K4 and K5 . When points A and B are maintained at different temperatures, no heat flows through the central rod if

View SolutionThe end of two rods of different materials with their thermal conductivities, area of cross-section and lengths all in the ratio 1:2 are maintained at the same temperature difference. If the rate of flow of heat in the first rod is 4cal/s. Then, in the second rod rate of heat flow in cal/s will be
View Solution