An iron ball has a diameter of 6cm and is 0.010mm too large to pass through a hole in a brass plate when the ball and plate are at a temperature of 30∘C. At what temperature, the same for ball and plate, will the ball just pass through the hole?
Take the values of (prop) from Table 20.2.
The correct Answer is:C
To solve the problem, we need to determine the temperature at which the iron ball will just pass through the hole in the brass plate. The diameter of the iron ball is 6 cm, and it is currently 0.010 mm too large to pass through the hole at 30°C.
1. Convert Measurements:
- The diameter of the iron ball is given as 6 cm. We convert this to millimeters:
6cm=60mm
- The ball is too large by 0.010 mm, so the effective diameter of the hole must be:
Diameter of hole=60mm−0.010mm=59.990mm
2. Understand Linear Expansion:
- The linear expansion of materials can be described by the formula:
ΔL=L⋅α⋅ΔT
- Where:
- ΔL = change in length (or diameter in this case)
- L = original length (or diameter)
- α = coefficient of linear expansion
- ΔT = change in temperature
3. Identify Coefficients of Linear Expansion:
- From the problem, we need the coefficients of linear expansion for brass and iron:
- αbrass=19×10−6°C−1
- αiron=12×10−6°C−1
4. Calculate the Effective Change in Diameter:
- The change in diameter of the ball and the hole must equal the initial difference of 0.010 mm:
ΔL=0.010mm=60⋅(αbrass−αiron)⋅(T−30)
5. Substituting Values:
- Substitute αbrass and αiron into the equation:
0.010=60⋅(19×10−6−12×10−6)⋅(T−30)
- Simplifying the coefficients:
0.010=60⋅(7×10−6)⋅(T−30)
6. Rearranging the Equation:
- Rearranging gives:
0.010=60⋅7×10−6⋅(T−30)
0.010=4.2×10−4⋅(T−30)
7. Solving for Temperature:
- Divide both sides by 4.2×10−4:
T−30=0.0104.2×10−4≈23.81
- Therefore,
T≈30+23.81≈53.81°C
8. Final Temperature:
- Rounding off gives:
T≈50.8°C
Conclusion:
The temperature at which the iron ball will just pass through the hole in the brass plate is approximately 50.8 °C.
- The diameter of the iron ball is given as 6 cm. We convert this to millimeters:
6cm=60mm
- The ball is too large by 0.010 mm, so the effective diameter of the hole must be:
Diameter of hole=60mm−0.010mm=59.990mm
- The linear expansion of materials can be described by the formula:
ΔL=L⋅α⋅ΔT
- Where:
- ΔL = change in length (or diameter in this case)
- L = original length (or diameter)
- α = coefficient of linear expansion
- ΔT = change in temperature
- From the problem, we need the coefficients of linear expansion for brass and iron:
- αbrass=19×10−6°C−1
- αiron=12×10−6°C−1
- The change in diameter of the ball and the hole must equal the initial difference of 0.010 mm:
ΔL=0.010mm=60⋅(αbrass−αiron)⋅(T−30)
- Substitute αbrass and αiron into the equation:
0.010=60⋅(19×10−6−12×10−6)⋅(T−30)
- Simplifying the coefficients:
0.010=60⋅(7×10−6)⋅(T−30)
- Rearranging gives:
0.010=60⋅7×10−6⋅(T−30)
0.010=4.2×10−4⋅(T−30)
- Divide both sides by 4.2×10−4:
T−30=0.0104.2×10−4≈23.81
- Therefore,
T≈30+23.81≈53.81°C
- Rounding off gives:
T≈50.8°C
The temperature at which the iron ball will just pass through the hole in the brass plate is approximately 50.8 °C.
Topper's Solved these Questions
- THERMOMETRY,THERMAL EXPANSION & KINETIC THEORY OF GASESBook:DC PANDEY ENGLISHChapter:THERMOMETRY,THERMAL EXPANSION & KINETIC THEORY OF GASESExercise:Exercise 20.3
Explore 7 Videos
- THERMOMETRY,THERMAL EXPANSION & KINETIC THEORY OF GASESBook:DC PANDEY ENGLISHChapter:THERMOMETRY,THERMAL EXPANSION & KINETIC THEORY OF GASESExercise:Exercise 20.4
Explore 3 Videos
- THERMOMETRY,THERMAL EXPANSION & KINETIC THEORY OF GASESBook:DC PANDEY ENGLISHChapter:THERMOMETRY,THERMAL EXPANSION & KINETIC THEORY OF GASESExercise:Exercise 20.1
Explore 5 Videos
- THERMOMETRY THERMAL EXPANSION AND KINETIC THEORY OF GASESBook:DC PANDEY ENGLISHChapter:THERMOMETRY THERMAL EXPANSION AND KINETIC THEORY OF GASESExercise:Medical entrance gallary
Explore 30 Videos
- UNIT AND DIMENSIONSBook:DC PANDEY ENGLISHChapter:UNIT AND DIMENSIONSExercise:Assertion And Reason
Explore 2 Videos
Similar Questions
A ball does not pass through a copper ring at room temperature. The same ball, after heating, passes through the same ring. It shows due to heating, the ball
View SolutionA cylindrical steel plug is inserted into a circular hole of diameter 2.60 cm in a brass plate. When the plug and the plates are at a temperature of 20∘C, the diameter of the plug is 0.010 cm smaller than that of the hole. The temperature at which the plug will just fit in it is
(Given,αsteel=11×10−6C−1andαbrass=19×10−6C−1
View SolutionAn aluminum plate fixed in a horizontal position has a hole of diameter 2.000 cm. A steel sphere of diameter 2.005 cm rests on this hole. All the lengths refer to a temperature of 10∘C.The temperature of the entire system is slowly increased. At what temperature will the ball fall down? coefficient of linear expansion of aluminum is 23×10−6C−1 and that of steel is 11×10−6C−1.
View SolutionA converging lens has a focal length of 30cm. Rays from a 2.0cm high filament that pass through the lens from a virtual image at a distance of 50cm from the lens. Where is the filament located? What is the height of the image?
View SolutionTwo recangular plates A and B placed at a distance 2a apart, are connected to a battery to produce an electric field. There are insulators between plantes C and other two plates. A magnetic field exists along z-axis. A charged particle of mass m and charge q passes through a hole at the middle of the plate A with velocity v and strikes at Q which is the middle of the bottom edge of plate B after passing through a hole inplate C. If E=mv2/qa, what will be the speed of the particle at Q?
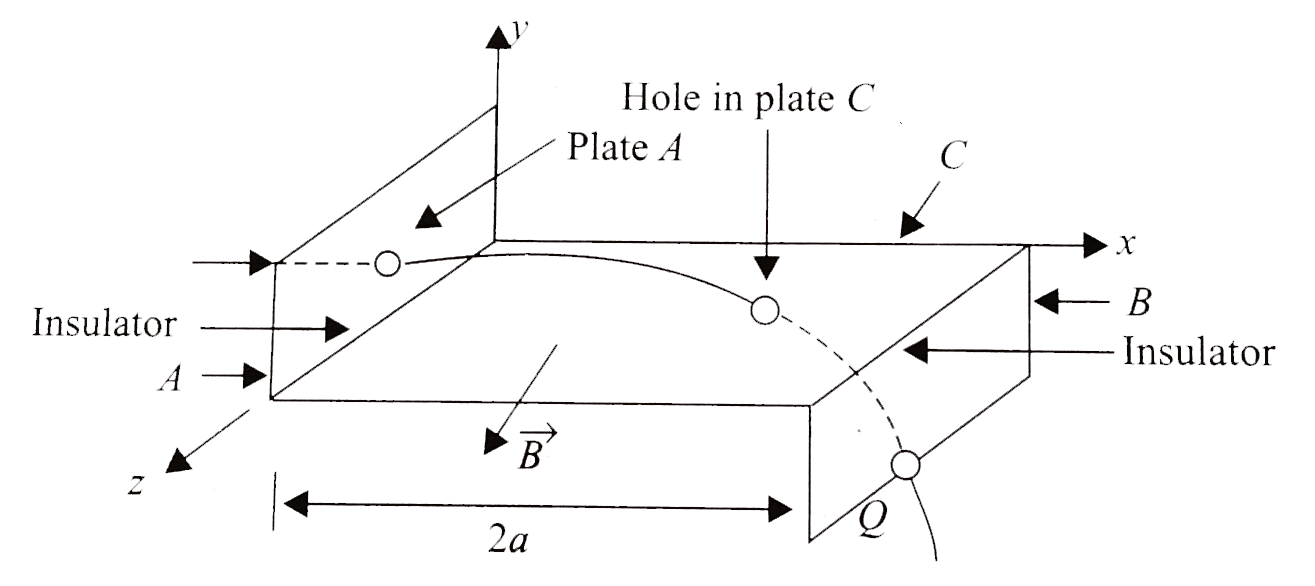
View SolutionTwo rings are suspended from the points A and B on the ceiling of a room with the help of strings of length 1.2 m each as shown. The points A and B are separated from each other by a distance AB = 1.2 m. A boy standing on the floor throws a small ball so that it passes through the two rings whose diameter is slightly greater than the ball. At the moment when the boy throws the ball, his hand is at a height of 1.0 m above the floor. A stop watch which is switched on at the moment of throwing the ball reads 0.2 s when the ball passes through the first ring and 0.6 s when it passes through the second ring.
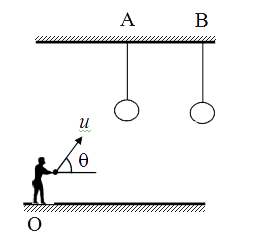
The angle of projection of the ball is:
View SolutionIn the figure shown a parallel plate capacitor is connected across a source of emf ε. The plates are square shaped with edge 'l' and separated by a distance d. A dielectric slab of dielectric constant k and thickness d is inserted between the plates with constant speed v. Find the current in the connecting wires, ignore the resistance of connecting wires. A current of equal strength is passed through a coil of resistance R and dipped into water kept in a bucket at 0∘C. What would be the temperature of the water at the end of 5 minutes if mass of the water is m and specific heat of the water is c?

View SolutionA carpenter builds an outer house wall with a layer of wood 2.0 cm thick on the outside and a layer of an insulation 3.5 cm thick as the inside wall surface. The wood has K=0.08W/m.K and the insulation has K=0.01W/m.K . The interior surface temperature is 19∘C and the exterior surface temperature is −10∘C.
(a) What is the temperature at the plane where the wood meets the insulation?
(b) What is the rate of heat flow per square metre through this wall ?
View SolutionTwo rings are suspended from the points A and B on the ceiling of a room with the help of strings of length 1.2 m each as shown. The points A and B are separated from each other by a distance AB = 1.2 m. A boy standing on the floor throws a small ball so that it passes through the two rings whose diameter is slightly greater than the ball. At the moment when the boy throws the ball, his hand is at a height of 1.0 m above the floor. A stop watch which is switched on at the moment of throwing the ball reads 0.2 s when the ball passes through the first ring and 0.6 s when it passes through the second ring.

When the ball lands on the floor, the stop watch reads:
View SolutionTwo rings are suspended from the points A and B on the ceiling of a room with the help of strings of length 1.2 m each as shown. The points A and B are separated from each other by a distance AB = 1.2 m. A boy standing on the floor throws a small ball so that it passes through the two rings whose diameter is slightly greater than the ball. At the moment when the boy throws the ball, his hand is at a height of 1.0 m above the floor. A stop watch which is switched on at the moment of throwing the ball reads 0.2 s when the ball passes through the first ring and 0.6 s when it passes through the second ring.
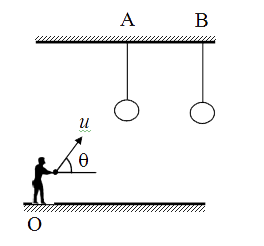
The maximum height attained by the ball above the floor is:
View Solution

