An organ pipe P1 open at one end vibrating in its first harmonic and another pipe P2 open at ends vibrating in its third harmonic are in resonance with a given tuning fork. The ratio of the length of P1 to that P2 is
The correct Answer is:C
To find the ratio of the lengths of the two organ pipes P1 and P2, we need to use the principles of harmonics for open and closed pipes.
1. Understanding the Harmonics:
- For an organ pipe open at one end (like P1), the fundamental frequency (first harmonic) is given by:
f1=V4L1
- For an organ pipe open at both ends (like P2), the frequency for the third harmonic is given by:
f2=3V2L2
2. Setting Up the Resonance Condition:
- Since both pipes are in resonance with the same tuning fork, we can set their frequencies equal:
f1=f2
- Substituting the expressions for f1 and f2:
V4L1=3V2L2
3. Eliminating V:
- We can cancel V from both sides (assuming V≠0):
14L1=32L2
4. Cross-Multiplying:
- Cross-multiply to solve for the relationship between L1 and L2:
2L2=12L1
5. Finding the Ratio:
- Rearranging gives:
L1L2=212=16
Final Answer:
The ratio of the length of P1 to that of P2 is:
L1L2=16
- For an organ pipe open at one end (like P1), the fundamental frequency (first harmonic) is given by:
f1=V4L1
- For an organ pipe open at both ends (like P2), the frequency for the third harmonic is given by:
f2=3V2L2
- Since both pipes are in resonance with the same tuning fork, we can set their frequencies equal:
f1=f2
- Substituting the expressions for f1 and f2:
V4L1=3V2L2
- We can cancel V from both sides (assuming V≠0):
14L1=32L2
- Cross-multiply to solve for the relationship between L1 and L2:
2L2=12L1
- Rearranging gives:
L1L2=212=16
The ratio of the length of P1 to that of P2 is:
L1L2=16
Topper's Solved these Questions
- SOUND WAVESBOOK - DC PANDEY ENGLISHCHAPTER - SOUND WAVESEXERCISE - INTRODUCTORY EXERCISE
1 Video
- SOUND WAVESBOOK - DC PANDEY ENGLISHCHAPTER - SOUND WAVESEXERCISE - Exercise 19.6
2 Videos
- SOUND WAVESBOOK - DC PANDEY ENGLISHCHAPTER - SOUND WAVESEXERCISE - Exercise 19.4
2 Videos
- SOLVD PAPERS 2017 NEET, AIIMS & JIPMERBOOK - DC PANDEY ENGLISHCHAPTER - SOLVD PAPERS 2017 NEET, AIIMS & JIPMEREXERCISE - Solved paper 2018(JIPMER)
38 Videos
- SUPERPOSITION OF WAVESBOOK - DC PANDEY ENGLISHCHAPTER - SUPERPOSITION OF WAVESEXERCISE - Level 2 Subjective
8 Videos
Similar Questions
An organ pipe P1 closed at one end and vibrating in its first overtone, and another pipe P2 open at both ends and vibrating in its third overtone, are in resonance with a given tuning fork. The ratio of the length of P1 to that of P2 is
View SolutionAn organ pipe A closed at one end vibrating in its fundamental frequency and another pipe B open at both ends is vibrating in its second overtone are in resonance with a given tuning fork . The ratiio of length of pipe A to that of B is
View SolutionAn organ pipe open at one end is vibrating in first overtone and is in resonance with another pipe open at both ends and vibrating in third harmonic. The ratio of length of two pipes is–
View SolutionAn open organ pipe of length L vibrates in its second harmonic mode. The correct statement about the Pressure variation is
View SolutionThird overtone of a closed organ pipe is in unison with fourth harmonic of an open organ pipe . Find the ratio of the lengths of the pipes.
View SolutionA massless uniform rod is subjected to froce F at its free end as shown in figure. The ratio of tensile stress at plane P1 to stress at P2 is
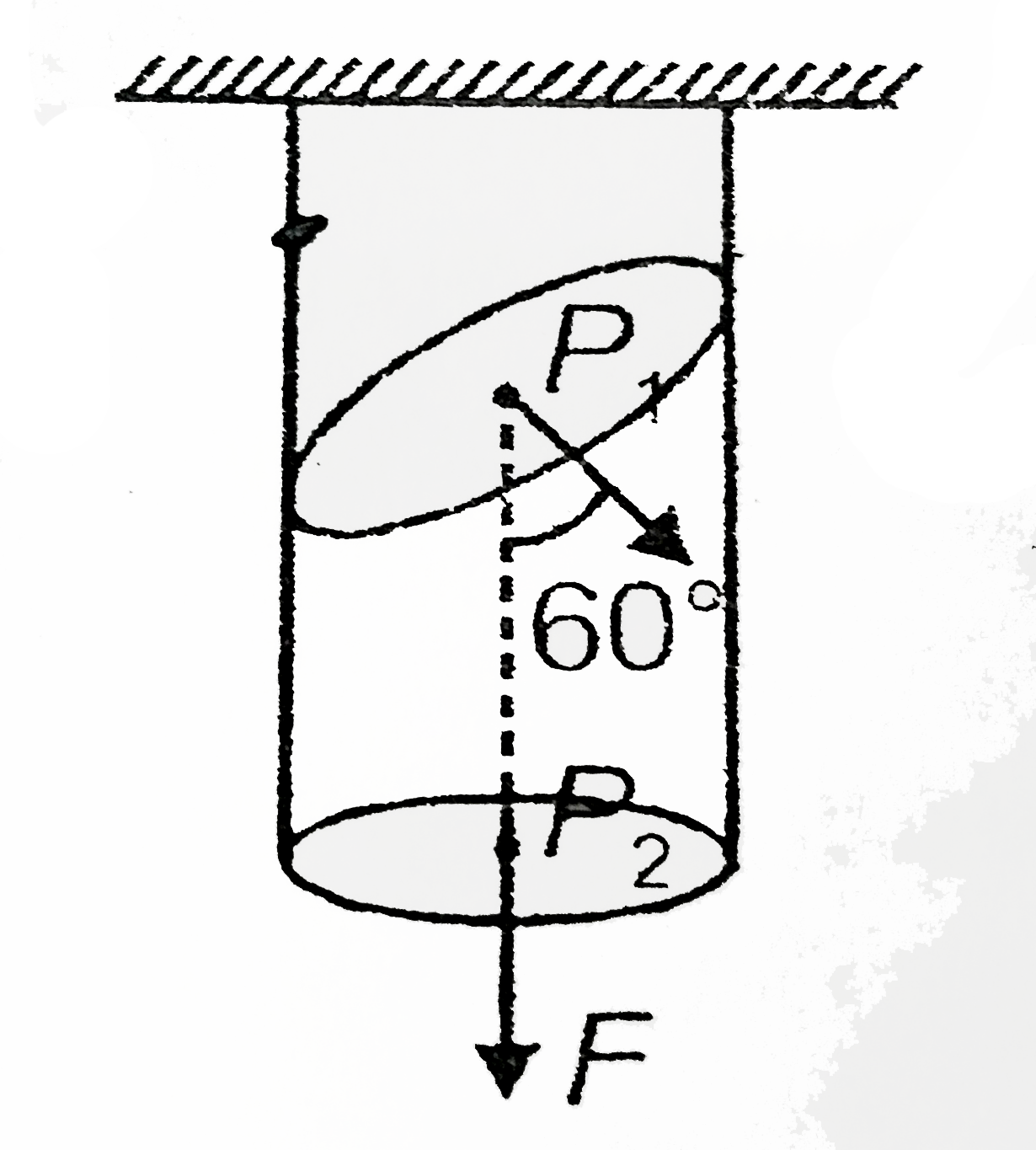
View SolutionAn air column in pipe, which is closed at one end, will be in resonance with a vibrating tuning fork of frequency 264Hz if the length of the column in cm is :
View SolutionA sonometer wire having a length of 1.50 m between the bridges vibrates in its second harmonic in resonance with a tuning fork of frequency 256 Hz. What is the speed of the transverse wave on the wire ?
View SolutionThird overtone of a closed organ pipe is in unison with fourth harmonic of an open organ pipe. Find the ratio of lengths of the two pipes.
View SolutionA tuning fork produces resonance at length 27 cm of a pipe closed at one end. Calculate the length of the pipe open at both ends which will produce resonance with the same tuning fork.
View Solution
