A vehicle , with a horn of frequency n is moving with a velocity of 30m/s in a direction prependicular to the straight line joining the observer and the vehicle . The observer perceives the sound to have a grequency (n+n1) . If the sound velocity in air is 330m/s , then
n1=10n
n1=0
n1=0.1n
n1=−0.1n
The correct Answer is:B
To solve the problem, we need to determine the change in frequency (n1) perceived by the observer when the vehicle is moving with a horn of frequency n. Here's a step-by-step breakdown of the solution:
Step 1: Understand the Scenario
We have a vehicle emitting sound at a frequency n and moving with a velocity of 30m/s perpendicular to the line joining the observer and the vehicle. The speed of sound in air is given as 330m/s.
Step 2: Identify the Apparent Frequency Formula
The apparent frequency f′ perceived by the observer can be calculated using the Doppler effect formula. However, since the source is moving perpendicular to the line of sight, the formula simplifies. The apparent frequency is given by:
f′=f⋅vv−vs
Where:
- f′ is the apparent frequency.
- f is the original frequency (n).
- v is the speed of sound in air (330 m/s).
- vs is the speed of the source (30 m/s).
Step 3: Apply the Formula
Since the source is moving perpendicular to the observer, the effective frequency perceived by the observer does not change due to the Doppler effect in this specific case. Thus, we can consider:
f′=f=n
Step 4: Relate Apparent Frequency to the Given Condition
According to the problem, the observer perceives the sound to have a frequency f′=n+n1. Since we established that f′=n:
n=n+n1
Step 5: Solve for n1
Rearranging the equation gives:
n−n=n1
This simplifies to:
n1=0
Conclusion
The value of n1 is 0.
Final Answer
Thus, the frequency perceived by the observer is the same as the emitted frequency, and n1=0.
---
We have a vehicle emitting sound at a frequency n and moving with a velocity of 30m/s perpendicular to the line joining the observer and the vehicle. The speed of sound in air is given as 330m/s.
The apparent frequency f′ perceived by the observer can be calculated using the Doppler effect formula. However, since the source is moving perpendicular to the line of sight, the formula simplifies. The apparent frequency is given by:
- f′ is the apparent frequency.
- f is the original frequency (n).
- v is the speed of sound in air (330 m/s).
- vs is the speed of the source (30 m/s).
Since the source is moving perpendicular to the observer, the effective frequency perceived by the observer does not change due to the Doppler effect in this specific case. Thus, we can consider:
According to the problem, the observer perceives the sound to have a frequency f′=n+n1. Since we established that f′=n:
Rearranging the equation gives:
The value of n1 is 0.
Thus, the frequency perceived by the observer is the same as the emitted frequency, and n1=0.
Topper's Solved these Questions
- SOUND WAVESBOOK - DC PANDEY ENGLISHCHAPTER - SOUND WAVESEXERCISE - Level 1 Subjective
45 Videos
- SOUND WAVESBOOK - DC PANDEY ENGLISHCHAPTER - SOUND WAVESEXERCISE - Subjective Questions
1 Video
- SOUND WAVESBOOK - DC PANDEY ENGLISHCHAPTER - SOUND WAVESEXERCISE - Level 1 Assertion And Reason
10 Videos
- SOLVD PAPERS 2017 NEET, AIIMS & JIPMERBOOK - DC PANDEY ENGLISHCHAPTER - SOLVD PAPERS 2017 NEET, AIIMS & JIPMEREXERCISE - Solved paper 2018(JIPMER)
38 Videos
- SUPERPOSITION OF WAVESBOOK - DC PANDEY ENGLISHCHAPTER - SUPERPOSITION OF WAVESEXERCISE - Level 2 Subjective
8 Videos
Similar Questions
A vehicle, with a horn of frequency n is moving with a velocity of 30 m/s in a direction perpendicular to the straight line joining the observer and the vehicle. The observer perceives the sound to have a frequency n+n1. Then (if the sound velocity in air is 300 m/s)
View SolutionThe source (S) of sound is moving constant velocity v0 as shown in diagram. An observer O listens to the sound emmited by the source. The observed frequency of the sound
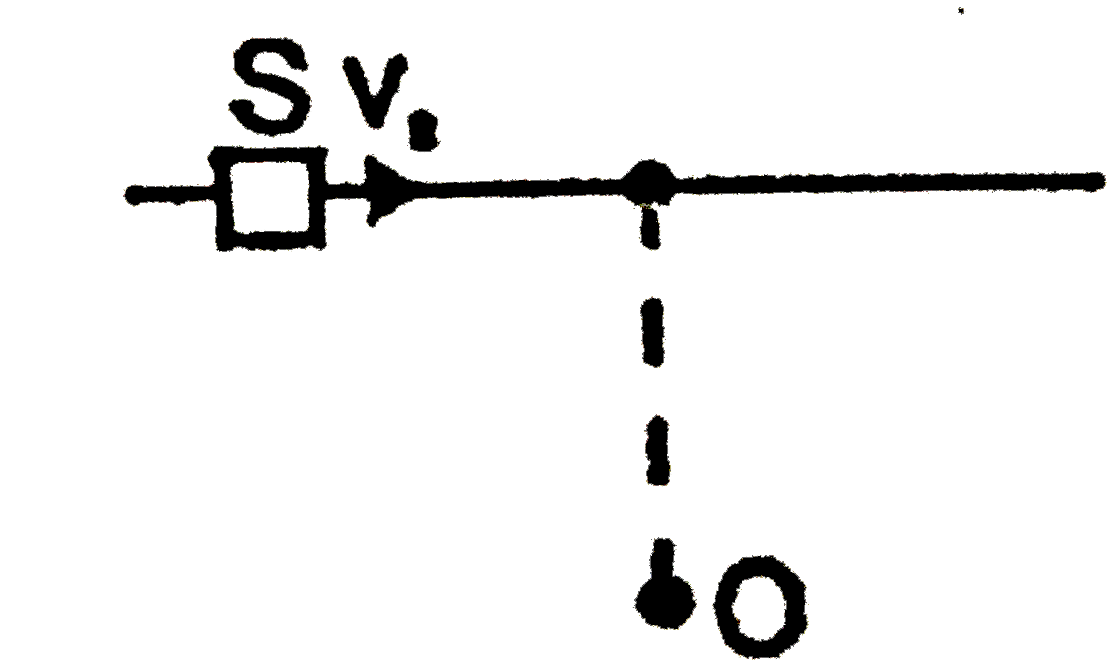
View SolutionDoppler shift in frequency of sound is independent of (Source is moving on the straight line joining source and observer)
View SolutionA source of sound of frequency 500 Hz is moving towards an observer with velocity 30 m/s . The speed of sound is 330 m/s . the frequency heard by the observer will be
View SolutionAn engine blowing a whistle of frequency 133 Hz moves with a velocity of 60ms towards a hill from which an echo is heard. Calculate the frequency of the echo heard by the driver. (velocity of sound in air in 340ms.)
View Solution
A tuning fork of frequency 380 Hz is moving towards a wall with a velocity of 4ms Then the number of beats heard by a stationary listener between direct and reflected sound will be (velocity of sound in air is 340ms)
View SolutionAn engine blowing a whistle of frequency 133 Hz moves with a velocity of 60ms towards a wall from which an echo is heard. Calculate the frequency of the echo heard by the driver. (velocity of sound in air in 340ms.)
View SolutionA vehicle sounding a whistle of frequency 256Hz is moving on a straight road,towards a hill with velocity of 10ms−1. The number of beats per second observed by a person travelling in the vehicle is (velocity of sound = 300ms−1
View SolutionA source of sound which emitting a sound of frequency 600 Hz is moving towards a wall with a velocity 30 m/s. Three observes A, B, C moving with velocity 20 m/s, A away from the wall and B towards the wall and Inside the source, Velocity of sound in air is 330 m/s.
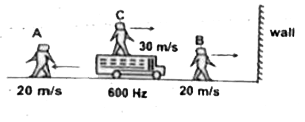
Find the frequency of direct sound observed by observer A
View SolutionA source of sound which emitting a sound of frequency 600 Hz is moving towards a wall with a velocity 30 m/s. Three observes A, B, C moving with velocity 20 m/s, A away from the wall and B towards the wall and Inside the source, Velocity of sound in air is 330 m/s.

Frequency of directed sound observer by observer C.
View Solution
