Sound waves of frequency 660HZ fall normally on perfectly reflecting wall. The distance from the wall at which the air particles have the maximum amplitude of vibration is (speed of sound in air = 330m/s)
The correct Answer is:A, B
To solve the problem, we need to determine the distance from the wall at which the air particles have the maximum amplitude of vibration when sound waves of frequency 660 Hz fall normally on a perfectly reflecting wall. The speed of sound in air is given as 330 m/s.
1. Identify the Properties of the Wave:
- Frequency (f) = 660 Hz
- Speed of sound (v) = 330 m/s
2. Calculate the Wavelength (λ):
- We use the formula that relates speed, frequency, and wavelength:
v=f⋅λ
- Rearranging the formula to find the wavelength:
λ=vf
- Substituting the known values:
λ=330m/s660Hz=0.5m
3. Identify the Node and Antinode:
- At the wall (reflecting surface), there is a node (point of no displacement).
- The first antinode (point of maximum displacement) occurs at a distance of λ4 from the wall.
4. Calculate the Distance to the First Antinode:
- We calculate the distance from the wall to the first antinode:
Distance to antinode=λ4=0.5m4=0.125m
- Converting to a fraction:
0.125m=18m
5. Final Answer:
- The distance from the wall at which the air particles have the maximum amplitude of vibration is 18m.
Summary:
The distance from the wall at which the air particles have the maximum amplitude of vibration is 18m.
---
- Frequency (f) = 660 Hz
- Speed of sound (v) = 330 m/s
- We use the formula that relates speed, frequency, and wavelength:
v=f⋅λ
- Rearranging the formula to find the wavelength:
λ=vf
- Substituting the known values:
λ=330m/s660Hz=0.5m
- At the wall (reflecting surface), there is a node (point of no displacement).
- The first antinode (point of maximum displacement) occurs at a distance of λ4 from the wall.
- We calculate the distance from the wall to the first antinode:
Distance to antinode=λ4=0.5m4=0.125m
- Converting to a fraction:
0.125m=18m
- The distance from the wall at which the air particles have the maximum amplitude of vibration is 18m.
The distance from the wall at which the air particles have the maximum amplitude of vibration is 18m.
Topper's Solved these Questions
- SUPERPOSITION OF WAVESBOOK - DC PANDEY ENGLISHCHAPTER - SUPERPOSITION OF WAVESEXERCISE - Exercise 18.4
3 Videos
- SUPERPOSITION OF WAVESBOOK - DC PANDEY ENGLISHCHAPTER - SUPERPOSITION OF WAVESEXERCISE - Level 1 Assertion And Reason
10 Videos
- SUPERPOSITION OF WAVESBOOK - DC PANDEY ENGLISHCHAPTER - SUPERPOSITION OF WAVESEXERCISE - Exercise 18.2
4 Videos
- SOUND WAVESBOOK - DC PANDEY ENGLISHCHAPTER - SOUND WAVESEXERCISE - Exercise 19.7
4 Videos
- THERMOMETRY THERMAL EXPANSION AND KINETIC THEORY OF GASESBOOK - DC PANDEY ENGLISHCHAPTER - THERMOMETRY THERMAL EXPANSION AND KINETIC THEORY OF GASESEXERCISE - Medical entrance gallary
30 Videos
Similar Questions
Distance travelled by the sound produced by a tuning fork of frequency 50 Hz completing 200 vibrations is, (the velocity of sound in air is 330 m/s)
View Solution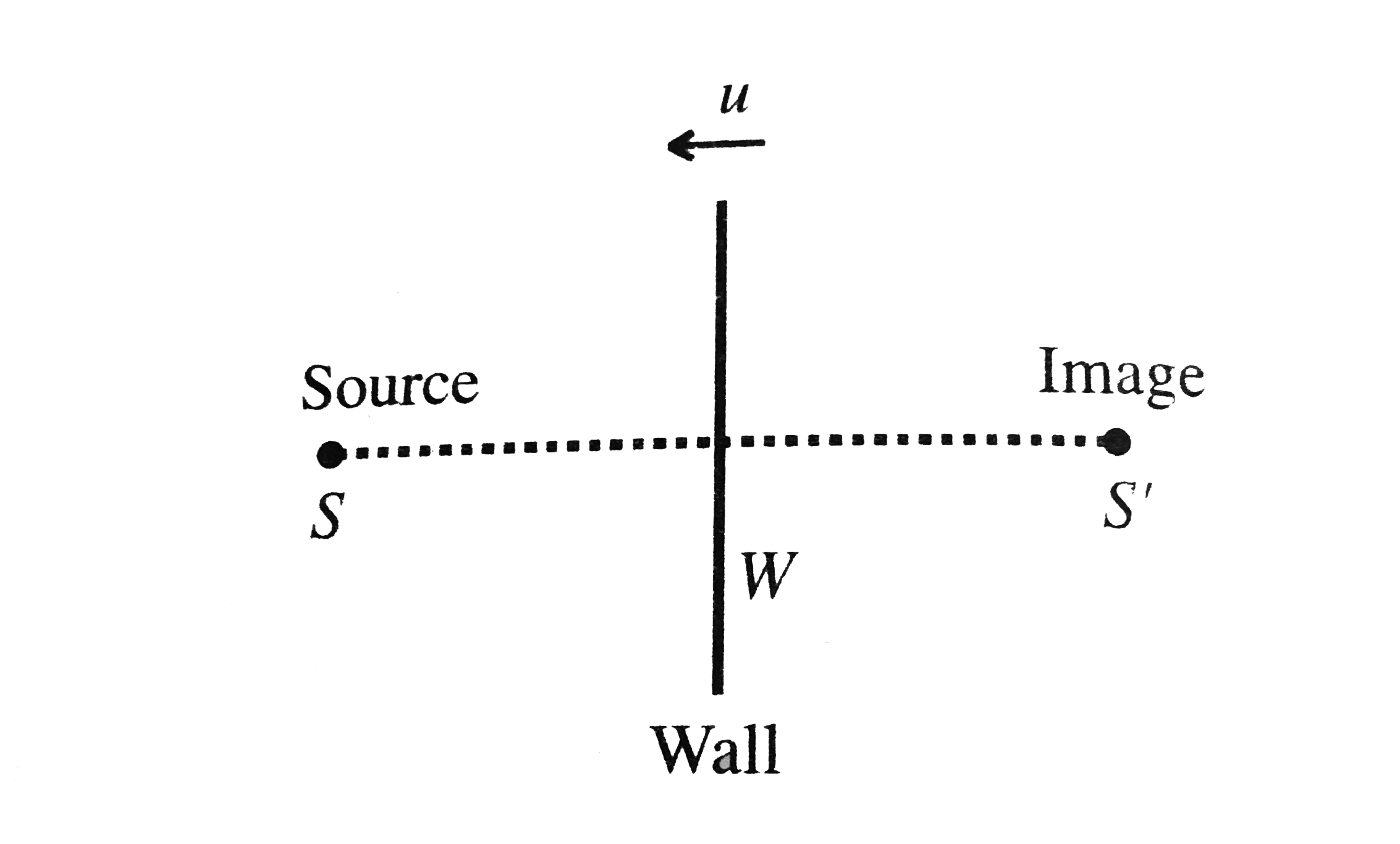 A driver in a stationary car horns which produces monochromatic sound waves of frequency n=1000Hz, normally towards a reflecting wall. If the wall approaches the car will a velocity u=3.3ms, calculate the frequency of sound reflected from wall and heard by the driver. What is the percentage change of sound frequency of reflection from the wall?
A driver in a stationary car horns which produces monochromatic sound waves of frequency n=1000Hz, normally towards a reflecting wall. If the wall approaches the car will a velocity u=3.3ms, calculate the frequency of sound reflected from wall and heard by the driver. What is the percentage change of sound frequency of reflection from the wall?
View SolutionA soure of sound of frequency 165 Hz generates sound waves which get fully reflected from a wall . A person standing at the wall starts moving away from the wall. The minimum distance of the point from the wall at which the person hears maximum sound is (velcoity of sound = 330 ms−1)
View SolutionA car blowing a horn of frequency 350 Hz is moving normally towards a wall a speed of 5 m/s The beat frequency heard by a person standing between the car and wall is (speed of sound in air =350 m/s )
View SolutionCalculate the minimum distance in air required between the source of sound and the obstacle to hear an echo. Take speed of sound in air = 350 ms−1
View SolutionA driver in a stationary car horns which produces sound waves having frequency 2000 Hz. The waves are directed normally towards a reflecting wall. If the wall approaches the car with a velocity u = 3.3 m/s. The change in the frequency of sound after reflection from the wall is x%. Then x
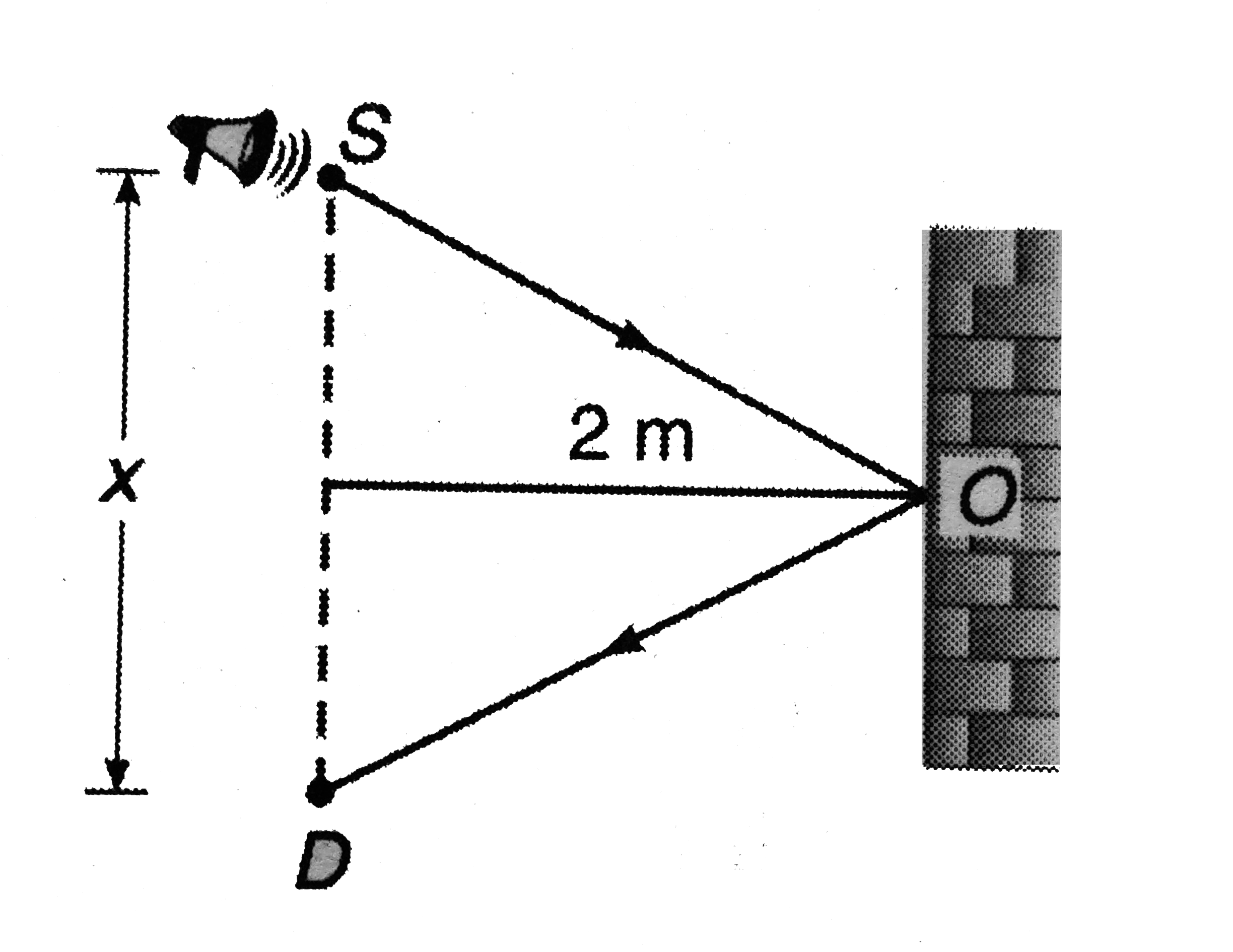
View SolutionA source of sound emitting waves at 360HZ is placed in front of a vertical wall, at a distance 2m from it. A detector is also placed in front of the wall at the same distance from it. Find the minimum distance between the source and the detestor for which the detector detects a maximum of sound. Take speed of sound in air=360m/s. Assume that there is not phase change in reflected wave.
View SolutionBus moving with speed v forwards a stationary wall. it produces sound of frequency f=420Hz.Theheardequencyofref≤ctedsoundomwallbydriveris490 Hz.Calca––tethespeedvofbus.Thevelocityofsound∈airis330 m/s.
View SolutionA man standing 25 m away from a wall produces a sound and receives the reflected sound.
Calculate the time after which he receives the reflected sound if the speed of sound in air is 350 m s−1.
View SolutionA man standing 25 m away from a wall produces a sound and receives the reflected sound.
Calculate the time after which he receives the reflected sound if the speed of sound in air is 350ms−1.
View Solution
