Vibrations of period 0.25s propagate along a straight line at a velocity of 48cm/s. One second after the the emergence of vibrations at the intial point, displacement of the point, 47cm from it is found to be 3cm. [Assume that at intial point particle is in its mean position at t=0 and moving upwards]. Then,
amplitude of vibrations is 6cm
amplitude of vibrations is 3√2cm
amplitude of vibrations is 3cm
None of these
The correct Answer is:A
∵ ω=2πT=2π0.25
=8πrad/s
v=ωk
∴k=ωv=8π0.48=(503)πm−1
y=Asin(ωt−kx)
=Asin(8πt−503πx)
Put, y=3cm, t= 1s,x=0.47mshow∈gwe≥tA = 6 cm
Topper's Solved these Questions
- WAVE MOTIONBook:DC PANDEY ENGLISHChapter:WAVE MOTIONExercise:Level 2 More Than One Correct
Explore 6 Videos
- WAVE MOTIONBook:DC PANDEY ENGLISHChapter:WAVE MOTIONExercise:Level 2 Subjective
Explore 7 Videos
- WAVE MOTIONBook:DC PANDEY ENGLISHChapter:WAVE MOTIONExercise:Level 1 Subjective
Explore 17 Videos
- VECTORSBook:DC PANDEY ENGLISHChapter:VECTORSExercise:Medical enrances gallery
Explore 9 Videos
- WORK, ENERGY & POWERBook:DC PANDEY ENGLISHChapter:WORK, ENERGY & POWERExercise:Level 2 Comprehension Based
Explore 2 Videos
Similar Questions
A tiny mass performs S.H.M along a straight line with a time period of T=0.60sec and amplitude A=10.0cm. Calculate the mean velocity (in m/sec) in the time to displace by A2.
View SolutionA particle moving along straight line has velocity v=μs where s is in the displacement . If s=s0 then which of the following graph best represent s versus t
View SolutionThe velocity (v)-time (t) graph of a partide moving along a straight line is as shown in the figure. The displacement of the particle from t = 0 to t = 4 is
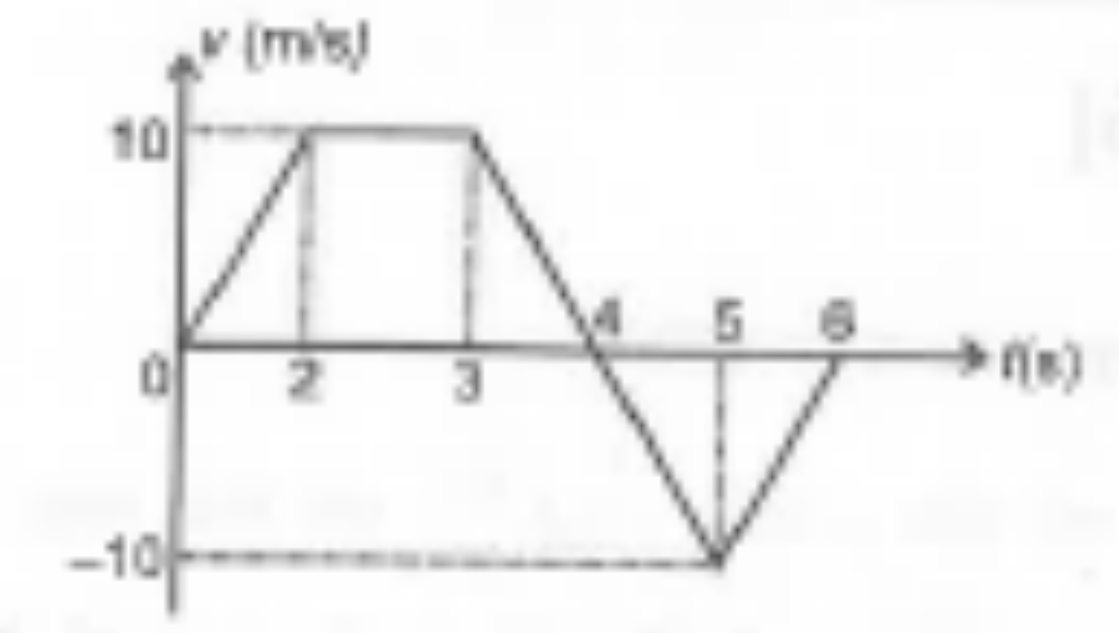
View SolutionA body executes S.H.M. of period 20 seconds. Its velocity is 5cms−1, 2 seconds after it has passed the mean position. Find the amplitude of the bob
(cos36∘=0.809)
View SolutionVelocity of a particle moving in a straight line varies with its displacement as v=(√4+4s)m/s. Displacement of particle at time t=0 is s=0. Find displacement of particle at time t=2s.
View SolutionA 2 m-long string fixed at both ends is set into vibrations in its first overtone. The wave speed on the string is 200 m s and the amplitude is 0.5 cm. (a) Find the wavelength and the frequency. (b) Write the equation giving the displacement of different points as a function of time. Choose the X-axis along the string with the origin at one end and t = 0 at the instant when the point x= 50 cm has reached its maximum displacement.
View SolutionA particle moving along a straight line with uniform acceleration has velocities 7m/s at A and 17m/s at C. B is the mid point of AC. Then :-
View SolutionA particle starts motion from rest and moves along a straight line. Its velocity-time graph is shown. Find out speed of particle at t=2s and at t=3s.

View SolutionFor a particle moving in a straight line, the displacement of the particle at time t is given by
S=t3−6t2+3t+7
What is the velocity of the particle when its acceleration is zero?
View SolutionFor a particle moving in a straight line, the displacement of the particle at time t is given by
S=t3−6t2+3t+7
What is the velocity of the particle when its acceleration is zero?
View Solution

