The equation of a wave is given by along the x-axis. (All the quantities are expressed in SI units). The phase difference between the points separated by a distance of along x-axis is
The correct Answer is:B
To find the phase difference between two points separated by a distance of 10 m along the x-axis for the wave described by the equation Y=5sin(10π(t−0.01x)), we can follow these steps:
Step 1: Identify the wave equation
The given wave equation is:
Y=5sin(10π(t−0.01x))
Step 2: Rewrite the wave equation in standard form
The standard form of a wave equation is:
Y=Asin(ωt−kx)
From the given equation, we can see that:
- ω=10π
- k=10π×0.01=0.1π
Step 3: Determine the phase difference formula
The phase difference Δϕ between two points separated by a distance Δx is given by:
Δϕ=kΔx
Step 4: Substitute the values
We know:
- k=0.1π
- Δx=10m
Now, substituting these values into the phase difference formula:
Δϕ=(0.1π)(10)=1π
Step 5: Final result
Thus, the phase difference between the points separated by a distance of 10 m is:
Δϕ=π
Conclusion
The correct option is B: π.
---
The given wave equation is:
Y=5sin(10π(t−0.01x))
The standard form of a wave equation is:
Y=Asin(ωt−kx)
From the given equation, we can see that:
- ω=10π
- k=10π×0.01=0.1π
The phase difference Δϕ between two points separated by a distance Δx is given by:
Δϕ=kΔx
We know:
- k=0.1π
- Δx=10m
Δϕ=(0.1π)(10)=1π
Thus, the phase difference between the points separated by a distance of 10 m is:
Δϕ=π
The correct option is B: π.
Topper's Solved these Questions
- WAVE MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - WAVE MOTIONEXERCISE - Level 1 Subjective
17 Videos
- WAVE MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - WAVE MOTIONEXERCISE - Level 2 Single Correct
5 Videos
- WAVE MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - WAVE MOTIONEXERCISE - Objective Questions
1 Videos
- VECTORSBOOK - DC PANDEY ENGLISHCHAPTER - VECTORSEXERCISE - Medical enrances gallery
9 Videos
- WORK, ENERGY & POWERBOOK - DC PANDEY ENGLISHCHAPTER - WORK, ENERGY & POWEREXERCISE - Level 2 Comprehension Based
2 Videos
Similar Questions
The equation of a travelling wave is given as y=5sin10π(t−Q.01x), along the x-axis . Here, all quantities are in SI units. The phase difference between the points separated by a distance of 10m alond x-axis is
View SolutionThe displacement equation of a wave is y = 0.5 sin π(2+−0.01x) where x is in meter and t is in second. Find the frequency, amplitude, speeds and phase difference between two particles situated at a distance of 5 m from each other.
View Solution
Knowledge Check
For the travelling harmonic wave
y(x, t) = 2 cos2π(10t - 0.008x + 0.35) where X and Y are in cm and t is in s. The phase difference between oscillatory motion of two points separated by distance of 0.5 m isA0.2πradB0.4πradC0.6πradD0.8πrad
A plane progressive wave is given by y=3×10−7sin(8500t−25x), where t is in second y is in m. Find the amplitude, and phase difference between two points separated by a distance 0.01m.
View SolutionThe equation of a wave is y=4sin{π2(2t+x8)} where y , x are in cm and time in seconds. The phase difference between two position of the same particle which are occupied at time interval of 0.4 s is xπ×10−1 , what is the value of x ?
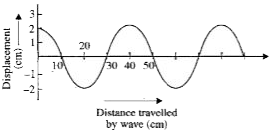
View SolutionA wave travelling along the length of a string is shown in Fig. 14.4.12. Using the scale on the given axis, find
(i) The amplitude of the wave
(ii) The wavelength of the wave
(iii) If the frequency of the wave is 10 Hz, What is the speed of the wave?
(iv) What is the initial phase of the wave ?
(v) What is the phase difference between two points separated by a distance 10 cm ?
(vi) If this wave is made to travel through water what is the wavelength of the wave, if the speed of, the waves in water is 10 m/s.
View SolutionThe equation of a transverse wave is given by
y=10sinπ(0.01x−2t)
where x and y are in cm and t is in second. Its frequency is
View SolutionThe equation of a simple harmonic progressive wave is given by y = A sin (100πt−3x) . Find the distance between 2 particles having a phase difference of π3.
View SolutionFor the harmonic travelling wave y=2cos2pi(10t-0.0080x+3.5) where x and y ar in cm and t is in second. What is the phase diffference between the oscillatory motion at two points separated by a distance of
View SolutionA travelling wave in a string is represented by y=3sin(π2t−π4x). The phase difference between two particles separated by a distance 4 cm is ( Take x and y in cm and t in seconds )
View Solution
