One end of a horizontal rope is attached to a prong of an electrically driven fork that vibrates at 120Hz. The other end passes over a pulley and supports a 1.50kg mass. The linear mass density of the rope is 0.0550kg/m.
(a) What is the speed of a transverse wave on the rope?
(b) Whatis the wavelength?
How would your answer to parts (a) and (b) change if the mass were increased to 3.00kg?
The correct Answer is:A, B, C
To solve the problem step by step, we will break it down into parts (a) and (b) as outlined in the question.
Part (a): Finding the Speed of the Transverse Wave on the Rope
1. Identify the Tension in the Rope:
The tension (T) in the rope is equal to the weight of the mass hanging from it. This can be calculated using the formula:
T=m⋅g
where:
- m=1.50kg (mass)
- g=9.81m/s2 (acceleration due to gravity)
Substituting the values:
T=1.50kg⋅9.81m/s2=14.715N
2. Calculate the Speed of the Wave:
The speed (v) of the transverse wave on the rope can be calculated using the formula:
v=√Tμ
where:
- μ=0.0550kg/m (linear mass density)
Substituting the values:
v=√14.715N0.0550kg/m
v=√267.545≈16.35m/s
Part (b): Finding the Wavelength
1. Use the Wave Speed and Frequency:
The wavelength (λ) can be calculated using the formula:
λ=vf
where:
- f=120Hz (frequency)
Substituting the values:
λ=16.35m/s120Hz≈0.13625m
Changes When the Mass is Increased to 3.00 kg
1. Calculate New Tension:
If the mass is increased to m=3.00kg:
T=3.00kg⋅9.81m/s2=29.43N
2. Calculate New Speed:
The new speed (v2) can be calculated as:
v2=√T2μ=√29.43N0.0550kg/m
v2=√535.636≈23.2m/s
3. Calculate New Wavelength:
The new wavelength (λ2) can be calculated as:
λ2=v2f=23.2m/s120Hz≈0.1933m
Summary of Results
- Part (a): Speed of the wave with 1.5 kg mass: ≈16.35m/s
- Part (b): Wavelength with 1.5 kg mass: ≈0.136m
- With 3.0 kg mass: Speed: ≈23.2m/s, Wavelength: ≈0.1933m
The tension (T) in the rope is equal to the weight of the mass hanging from it. This can be calculated using the formula:
T=m⋅g
where:
- m=1.50kg (mass)
- g=9.81m/s2 (acceleration due to gravity)
T=1.50kg⋅9.81m/s2=14.715N
The speed (v) of the transverse wave on the rope can be calculated using the formula:
v=√Tμ
where:
- μ=0.0550kg/m (linear mass density)
v=√14.715N0.0550kg/m
v=√267.545≈16.35m/s
The wavelength (λ) can be calculated using the formula:
λ=vf
where:
- f=120Hz (frequency)
λ=16.35m/s120Hz≈0.13625m
If the mass is increased to m=3.00kg:
T=3.00kg⋅9.81m/s2=29.43N
The new speed (v2) can be calculated as:
v2=√T2μ=√29.43N0.0550kg/m
v2=√535.636≈23.2m/s
The new wavelength (λ2) can be calculated as:
λ2=v2f=23.2m/s120Hz≈0.1933m
- Part (a): Speed of the wave with 1.5 kg mass: ≈16.35m/s
- Part (b): Wavelength with 1.5 kg mass: ≈0.136m
- With 3.0 kg mass: Speed: ≈23.2m/s, Wavelength: ≈0.1933m
Topper's Solved these Questions
- WAVE MOTIONBook:DC PANDEY ENGLISHChapter:WAVE MOTIONExercise:Exercise 17.6
Explore 6 Videos
- WAVE MOTIONBook:DC PANDEY ENGLISHChapter:WAVE MOTIONExercise:Level 1 Assertion And Reason
Explore 10 Videos
- WAVE MOTIONBook:DC PANDEY ENGLISHChapter:WAVE MOTIONExercise:Exercise 17.4
Explore 2 Videos
- VECTORSBook:DC PANDEY ENGLISHChapter:VECTORSExercise:Medical enrances gallery
Explore 9 Videos
- WORK, ENERGY & POWERBook:DC PANDEY ENGLISHChapter:WORK, ENERGY & POWERExercise:Level 2 Comprehension Based
Explore 2 Videos
Similar Questions
What is the speed of a transverse wave in a rope of length 10 m and mass 80 gm under a tension of 80 N?
View SolutionA uniform rope of mass m and length L hangs from a celling. (a) Show that the speed of a transverse wave on the rope is a function of y, the distance from the lower end, and is given by t=2√L/g.
View SolutionIn an experiment of standing waves, a string 90cm long is attached to the prong of an electrically driven tuning fork that scillates perpendicular to the length of the string at a frequency of 60Hz. The mass of the string is 0.044kg. What tension (in newton) must the string be under (weights are attached to the other end) if it is to oscillate in four loops?
View SolutionOne end of 12.0m long rubber tube with a total mass of 0.9kg is fastened to a fixed support. A cord attached to the other end passes over a pulley and support an object with a mass of 5.0kg. The tube is struck a transverse blow at one end. Find the time required for the pulse to reach the other end.(g=9.8m/s2)
View SolutionOne end of a long string of linear mass density 10−2kgm−1 is connected to an electrically driven tuning fork of frequency 150 Hz. The other end passes over a pulley and is tied to a pan containig a mass of 90 kg. the pulley end absorbs all the incoming energy so that reflected waves from this end have neglidible amplitude , At t =0, the left end (fork end ) of the string is at x=0 has a transverse displacement of 2.5 cm and is moving along positive y-direction. the amplitude of the wave is 5 cm. write down the transverse displacement y (in cetimetres) as function of x(in metres) and t (in seconds ) that describes the wave on the string.
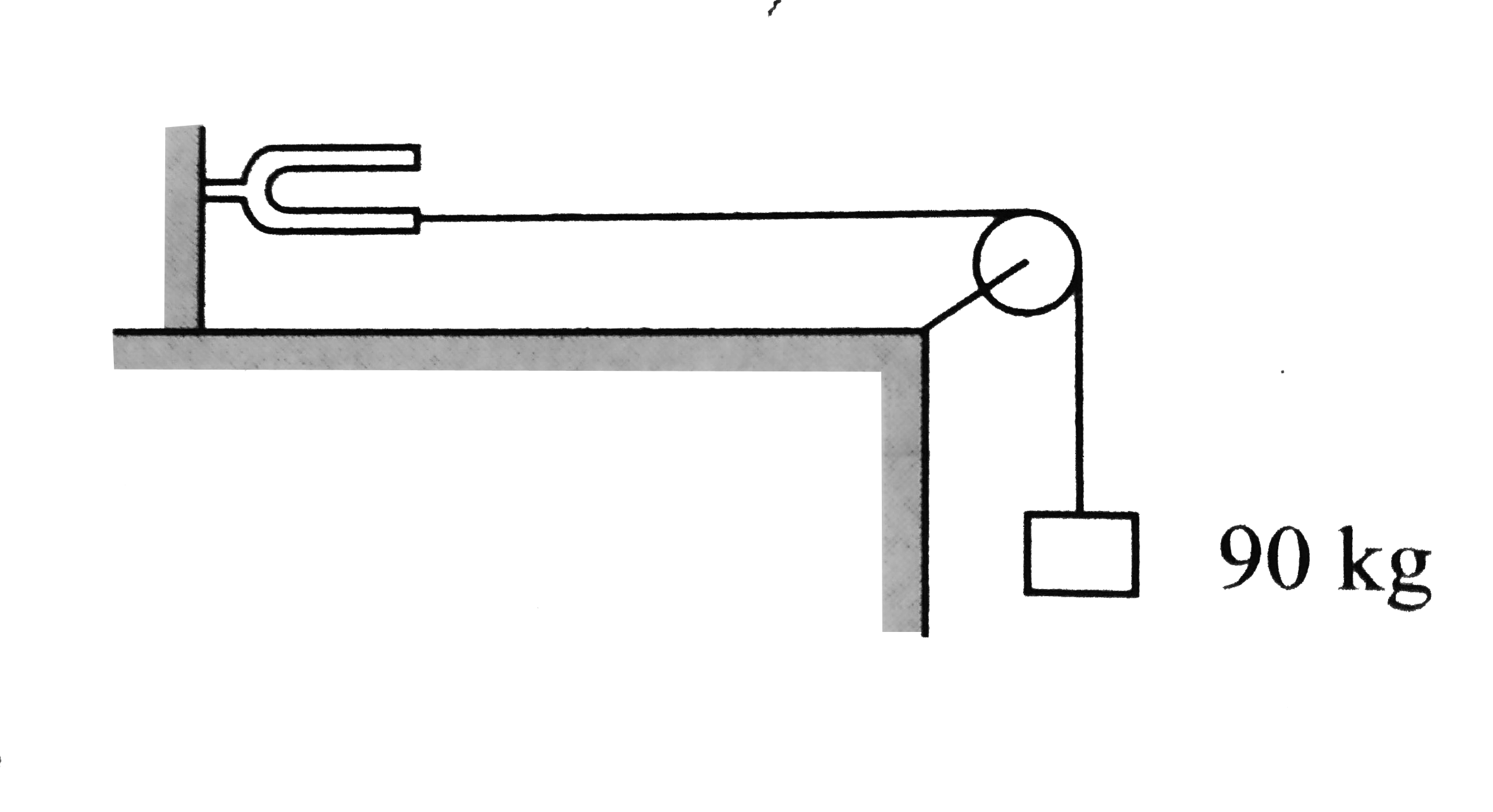
View SolutionOne end of a long string of linear mass dnesity 8.0×10−3kgm−1 is connected to an electrically driven tuning fork of frequency 256 Hz. The other end passes over a pulley and is tied to a pan containing a mass of 90 kg. The pulley end absorbs all the incoming energy so that reflected waves at this end have negligible amplitude. At t=0 the left end (fork end) of the string x=0 has zero transverse displacement (y=0) and is moving along positive y-direction. The amplitude of the wave is 5.0 cm. Write down the transverse displacement y as function of x and t that describest the wave on the string.
View SolutionA 1.50 m long rope is stretched between two supports with a tension that makes the speed of transverse waves 48.0m/s. What are the wavelength and frequency of
(a) the fundamental?
(b) the second overtone?
(c) the fourth harmonic?
View SolutionA uniform rope of length 12 mm and mass 6 kg hangs vertically from a rigid support. A block of mass 2 kg is attached to the free end of the rope. A transverse pulse of wavelength 0.06 m is produced at the lower end of the rope. What is the wavelength of the pulse when it reaches the top of the rope?
View SolutionA uniform rope of length 12 mm and mass 6 kg hangs vertically from a rigid support. A block of mass 2 kg is attached to the free end of the rope. A transverse pulse of wavelength 0.06 m is produced at the lower end of the rope. What is the wavelength of the pulse when it reaches the top of the rope?
View SolutionA uniform rope of length 10 cm and mass 4 kg hangs vertically from a rigid support. A block of mass 2 kg is attached to the free end of the rope. A transverse pulse of wavelength 0.06 m is produced at the lower end of the rope, what is the wavelength of the pulse when it reaches the top of the rope?
View Solution

