A streched string is forced to transmit transverse waves by means of an oscillator coupled to one end. The string has a diameter of 4mm. The amplititude of the oscillation is 10−4 m and the frequency is 10Hz. Tension in the string is 100 N and mass density of wire is 4.2×103kg/m3. Find
(a) the equation of the waves along the string
(b) the energy per unit volume of the wave
(c) the average energy flow per unit time across any section of the string and
(d) power required to drive the oscillator.
The correct Answer is:A, B, C, D
(a) Speed of transverse wave on the string is
v=√TρS (asμ=ρS)
Substituting the values,we have
v=
⎷100(4.2×103)(π4)(4.0×10−3)2=43.53m/s
ω=2πf=20π=62.83rad/s
k=ωv=1.44m−1
:. Equation of the waves along the string, y(x,t)=Asin(kx−ωt)
=(10−4m)sin[(1.44m−1)x−(62.83rade/s)t]
(b) Energy per unit volume of the string,u=energy density=12ρω2A2
Subsitutituting the values, we have
=u=(12)(4.2×103)(62.83)2(10−4)2
=8.29×10−2J/m3
(c) Average energy flow per unit time, P=power=(12ρω2A2)(Sv)=(u)(Sv)
Susbstituting the values, we have P=(8.29×10−2)(π4)(4×10−3)2(43.53)
4.53×10−5J/s
(d) Therefore, power required to drive the oscillator is 4.53×10−5W.
Topper's Solved these Questions
- WAVE MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - WAVE MOTIONEXERCISE - Example Type 1
1 Videos
- WAVE MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - WAVE MOTIONEXERCISE - Example Type 2
1 Videos
- VECTORSBOOK - DC PANDEY ENGLISHCHAPTER - VECTORSEXERCISE - Medical enrances gallery
9 Videos
- WORK, ENERGY & POWERBOOK - DC PANDEY ENGLISHCHAPTER - WORK, ENERGY & POWEREXERCISE - Level 2 Comprehension Based
2 Videos
Similar Questions
A transverse wave is travelling on a string. The equation of the wave
View SolutionA wire stretched between two rigid supports vibrates in its fundamental mode with a frequency of 45Hz. The mass of the wire is 3.5×10−2kg and its linear mass density is 4.0×10−2kgm−1. What is (a) the speed of a transverse wave on the string , and (b) the tension in the string?
View Solution
Knowledge Check
A wire is stretched between two rigid supports vibrates in its fundamental mode with a frequency of 50 Hz. The mass of the wire is 30 g and its linear density is 4×10−2 kg m s−1. The speed of the transverse wave at the string is
A25ms−1B50ms−1C75ms−1D100ms−1
When the tension in a string is increased by 44%. the frequency increased by 10Hz the frequency of the string is
View SolutionA string wave equation is given y = 0.002 sin(300t−15x) and mass density is (μ=0.1kgm). Then find the tension in the string
View SolutionThe equation of a transverse wave propagating in a string is given by
y=0.02sin(x+30t)
where, xandy are in second.
If linear density of the string is 1.3×10−4kg/m, then the tension in the string is
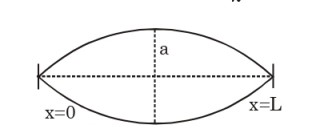
View SolutionA string of mass per unit length μ is clamped at both ends such that one end of the string is at x=0 and the other is at x=L. When string vibrates in fundamental mode, amplitude of the midpoint of string is a and tension in the string is F. Find the total oscillation energy (in J) stored in the string. (Use L=1 m, F = 10N, a = 1/pi m).
View SolutionThe velocity of waves in a string fixed at both ends is 2 m / s . The string forms standing waves with nodes 5.0 cm apart. The frequency of vibration of the string in Hz is
View SolutionA string of length L and mass M hangs freely from a fixed point . Calculate the velocity of the transverse wave along the string at any position.
(b)Calculate time taken by a transverse pulse to traverse the string.
View SolutionA piano string having a mass per unit length equal to 5.00×103kg/m is under a tension of 1350N, Find the speed with which a wave travels on this string.
View Solution
