A solid sphere a cone and a cylinder are floating in water. All have same mass, density and radius. Let f1f2,and f3 are the fraction of their volumes inside the water and h1,h2 and h3 are depths inside water. Then



f1=f2=f3
f3>f2>f1
h3<h1
h3<h2
The correct Answer is:A, C, D
Fraction of volume immersed in given by
f=ρsρl
ρs and ρl are same, Hence:
f1=f2=f3
Base area in third case is uniform. Hence h3 is minimum.
Topper's Solved these Questions
- FLUID MECHANICSBook:DC PANDEY ENGLISHChapter:FLUID MECHANICSExercise:Level 2 Comprehension Based
Explore 7 Videos
- FLUID MECHANICSBook:DC PANDEY ENGLISHChapter:FLUID MECHANICSExercise:Subjective
Explore 24 Videos
- FLUID MECHANICSBook:DC PANDEY ENGLISHChapter:FLUID MECHANICSExercise:Level 2 Single Correct
Explore 36 Videos
- EXPERIMENTSBook:DC PANDEY ENGLISHChapter:EXPERIMENTSExercise:Subjective
Explore 15 Videos
- GENERAL PHYSICSBook:DC PANDEY ENGLISHChapter:GENERAL PHYSICSExercise:INTEGER_TYPE
Explore 2 Videos
Similar Questions
Knowledge Check
The pressure P1 at the top of a dam and P2 at a depth h from the top inside water (density ρ) are related as :
AP1>P2BP1=P2CP1−P2=hρgDP2−P1=hρg
A solid sphere and a solid cylinder of same mass are rolled down on two inclined planes of heights h1 and h2 respectively. If at the bottom of the plane the two objects have same linear velocities, then the ratio of h1:h2 is
View SolutionA rubber ball floats on water with its 1/3rd volume outside water. What is the density of rubber?
View SolutionA point source of light is placed at a distance h below the surface of a large deep lake.
(a) Show that the fraction f of the light energy that escapes directly from the water surface is independent of h and is given by f=12−12n√n2−1 where n is the index of refraction of water.
(Note: Absorption within the water and reflection at the surface, except where it is total, have been neglected)
(b) Evaluate this ratio for n=4/3.
View SolutionA right circular cylinder and a right circular cone have the same radius and the same volume. The ratio of the height of the cylinder to that of the cone is (a) 3:5 (b) 2:5 (c) 3:1 (d) 1:3
View SolutionTwo cubical blocks identical in dimensions float in water in such a way that 1st block floats with half part immersed in water and second block floats with 3/4 of its volume inside the water. The ratio of densities of blocks is
View SolutionA thermometer uses density of water as thermometric property. Actual reading in thermometer is height of water (h) which inversely proportional to the density of water (d). In certain temp range is symmetrical ablout maximum.
Two identical bodies (of same mass and specific heat) at different temp T1 and T2 show the same reading of height h1=h2 in the thermometer. The bodies are brought in contact and allowed to reach the equilibrium. The thermometric reading height of water for final equilibrium state hf satisfies
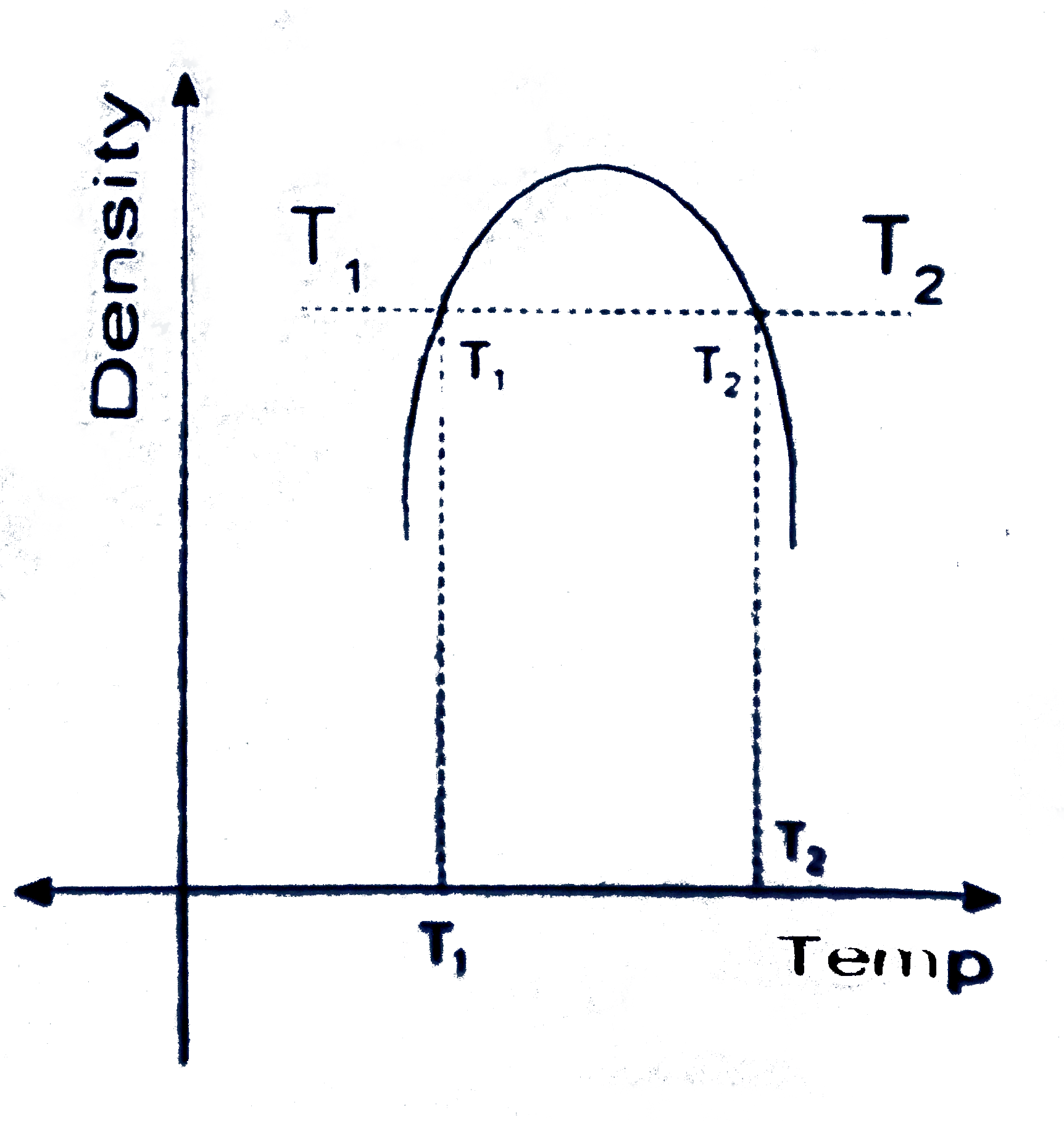
View SolutionAn ice berg floats on fresh water with a part of it outside the water surface. Calculate the fraction of the volume of the ice berg which is below the water surface. (Density of ice = 917kgm−3, Density of water = 1000kgm−3 )
View Solution

