A block in SHM starts from +A position. Write S−t equation of the block, if S is measured from −A.
S=A(1+cosωt)
S=2A(1+cosωt)
S=A(cosωt)
S=A(1+2cosωt)
The correct Answer is:A, C
To find the S−t equation of a block in Simple Harmonic Motion (SHM) that starts from the position +A, with S measured from −A, we can follow these steps:
Step 1: Understand the Initial Position
The block starts at position +A at time t=0. In SHM, the position x of the block can be described by the equation:
x(t)=Acos(ωt)
where A is the amplitude and ω is the angular frequency.
Step 2: Define the New Reference Point
Since S is measured from −A, we need to relate S to the position x. The distance S from −A to the block's position x can be expressed as:
S=x+A
This is because when the block is at −A, S will be zero.
Step 3: Substitute the Position Equation
Now, substitute the expression for x(t) into the equation for S:
S=(Acos(ωt))+A
Step 4: Simplify the Expression
Combine the terms:
S=A+Acos(ωt)
Factoring out A:
S=A(1+cos(ωt))
Final Equation
Thus, the equation relating S and t is:
S(t)=A(1+cos(ωt))
The block starts at position +A at time t=0. In SHM, the position x of the block can be described by the equation:
x(t)=Acos(ωt)
where A is the amplitude and ω is the angular frequency.
Since S is measured from −A, we need to relate S to the position x. The distance S from −A to the block's position x can be expressed as:
S=x+A
This is because when the block is at −A, S will be zero.
Now, substitute the expression for x(t) into the equation for S:
S=(Acos(ωt))+A
Combine the terms:
S=A+Acos(ωt)
Factoring out A:
S=A(1+cos(ωt))
Thus, the equation relating S and t is:
S(t)=A(1+cos(ωt))
Topper's Solved these Questions
- SIMPLE HARMONIC MOTIONBook:DC PANDEY ENGLISHChapter:SIMPLE HARMONIC MOTIONExercise:Example Type 9
Explore 1 Video
- SIMPLE HARMONIC MOTIONBook:DC PANDEY ENGLISHChapter:SIMPLE HARMONIC MOTIONExercise:Example Type 10
Explore 1 Video
- SIMPLE HARMONIC MOTIONBook:DC PANDEY ENGLISHChapter:SIMPLE HARMONIC MOTIONExercise:Example Type 7
Explore 1 Video
- SEMICONDUCTORS AND ELECTRONIC DEVICESBook:DC PANDEY ENGLISHChapter:SEMICONDUCTORS AND ELECTRONIC DEVICESExercise:More than One Option is Correct
Explore 3 Videos
- SOLVD PAPERS 2017 NEET, AIIMS & JIPMERBook:DC PANDEY ENGLISHChapter:SOLVD PAPERS 2017 NEET, AIIMS & JIPMERExercise:Solved paper 2018(JIPMER)
Explore 38 Videos
Similar Questions
Softest s-block metal is :-
View SolutionA block is performin SHM of amplitude 'A' in vertical direction. When block i8s at 'y' (measured from mean position), it detaches froms spring, so that spring contracts and does not effect the motion of the block. Find 'y⋅' such that block attains maximum height from the mean position. (given Aω2>g)
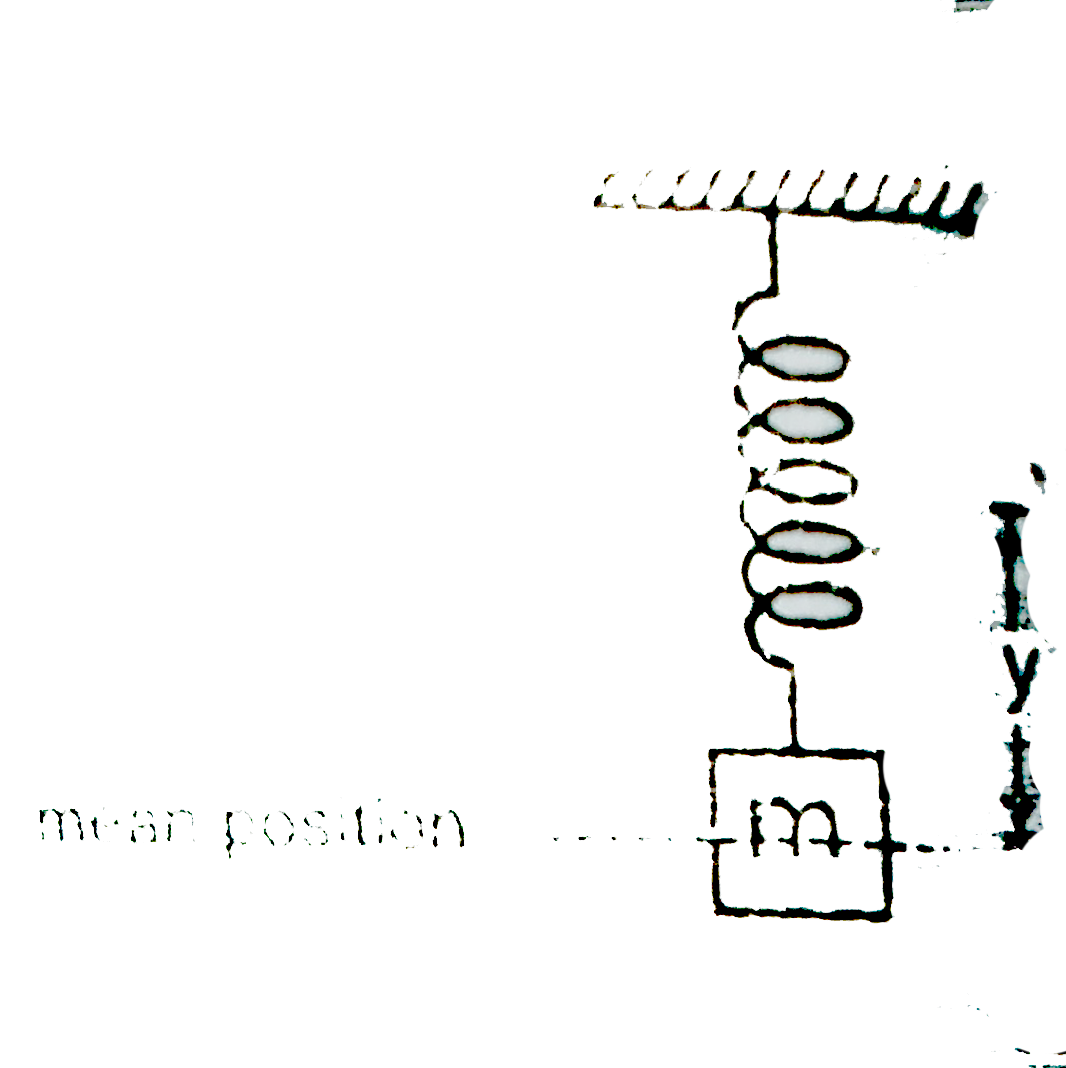
View SolutionA spring block system is kept inside the smooth surface of a trolley as shown in figure.

At t=0 trolley is given an acceleration 'a' in the direction shown in figure. Write S−t equation of the block
(a) with respect to trolley.
(b) with respect to ground.
View SolutionA 100g block is connected to a horizontal massless spring of force constant 25.6N/m. The block is free to oscillate on a horizontal fricationless surface. The block is displced by 3cm from the equilibrium position, and at t=0, it si released from rest at x=0, The position-time graph of motion of the block is shown in figure.
_S01_052_Q01.png)
Let us now make a slight change to the initial conditions. At t=0, let the block be released from the same position with an initial velocity v1=64cm/s. Position of the block as a function of time can be expressed as
View SolutionA 100g block is connected to a horizontal massless spring of force constant 25.6N/m. The block is free to oscillate on a horizontal fricationless surface. The block is displced by 3cm from the equilibrium position, and at t=0, it si released from rest at x=0, The position-time graph of motion of the block is shown in figure.
_S01_050_Q01.png)
When the block is at position A on the graph, its
View SolutionA block of mass 2.0 kg is pushed down an inclined plane of inclination 370 with a force of 20N acting parallel to the incline. It is found that the block moves on the incline with an acceleration of 10ms2. If the block started from rest, find the work done a. by the applied force in the first second b. by the weight of the block in the first second and c. by the frictional force acting on the block in the first second. Take g=10ms2.
View SolutionA constant force of 10 N act on a block as shown in figure initial velocity of the block is zero. It is observed from three frames of reference S1,S2 and ground. The frame S1 start from rest and move with constnat acceleration 10m/s2. The frames S1andS2 and block start moving simultaneously at t=0.
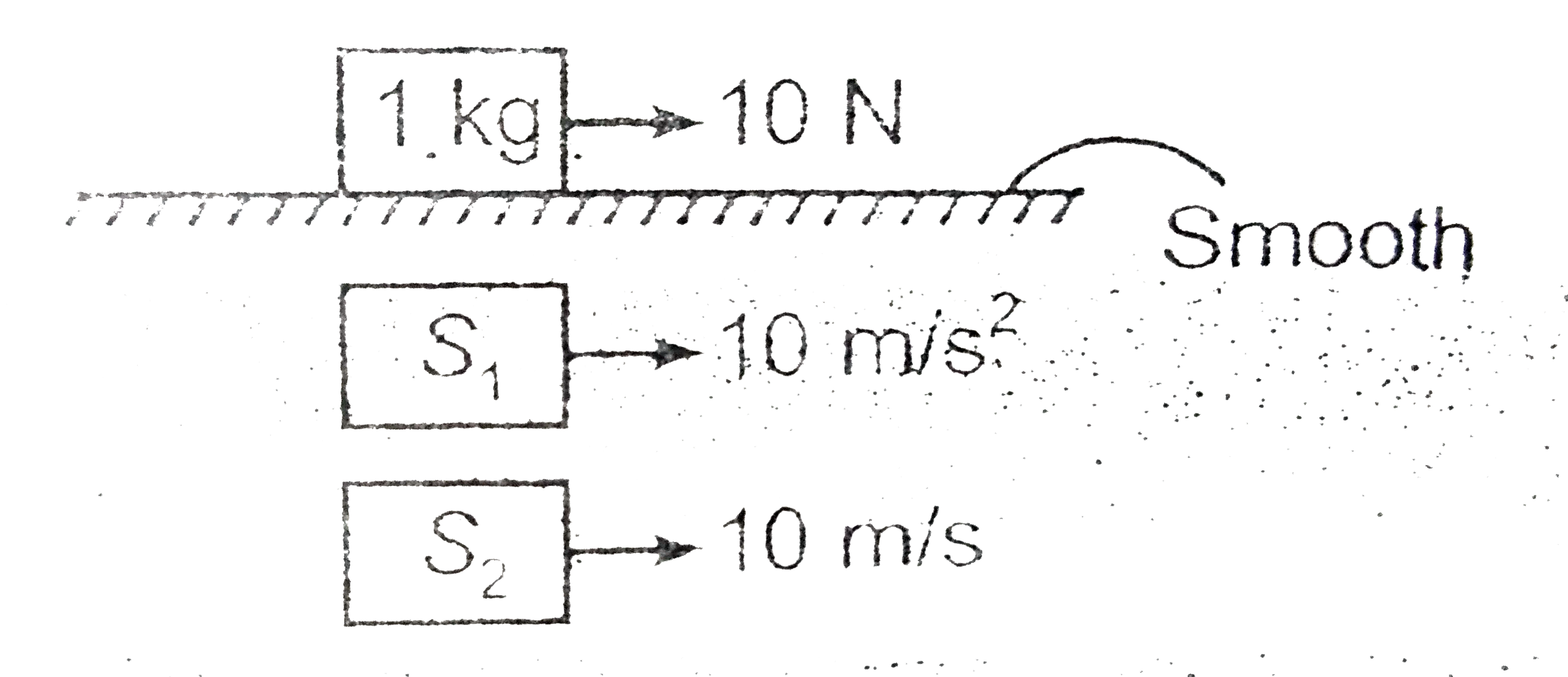
Net work done on block in 1 s as observed from frame S2 is
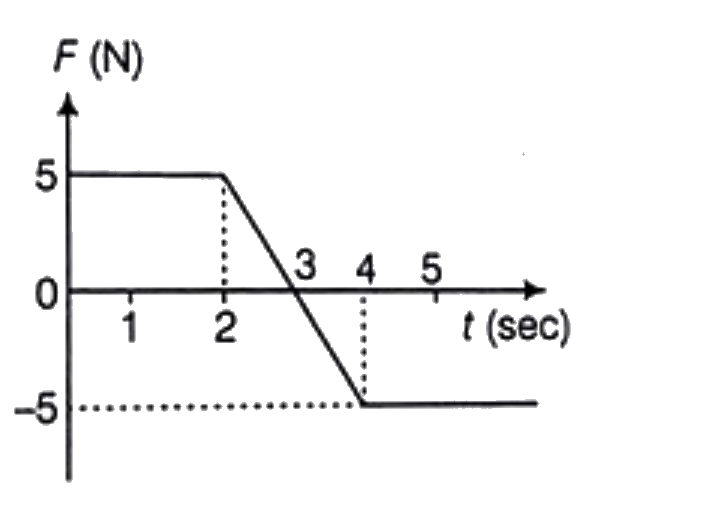
View SolutionA block of the mass of 1 kg is moving on the x-axis . A force F acting on the block is shown . The velocity of the block at time t = 2 s is - 3ms−1 what is the speed of the block at time t = 4 s?
View Solution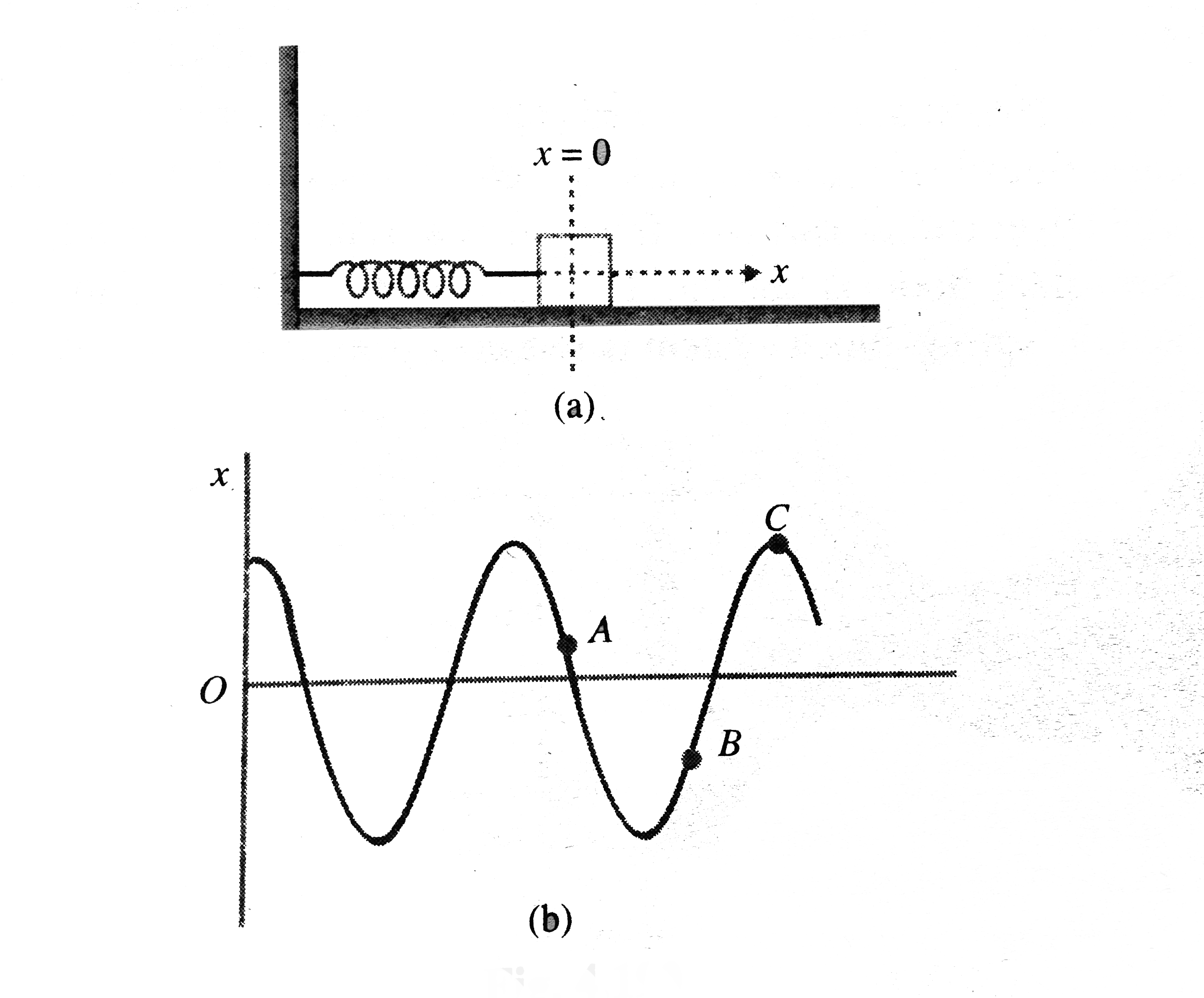
A 100 g block is connected to a horizontal massless spring of force constant 25.6Nm As shown in Fig. the block is free to oscillate on a horizontal frictionless surface. The block is displaced 3 cm from the equilibrium position and , at t=0, it is released from rest at x=0 It executes simple harmonic motion with the postive x-direction indecated in Fig. The position time (x−t) graph of motion of the block is as shown in Fig.
Q. When the block is at position B on the graph its.
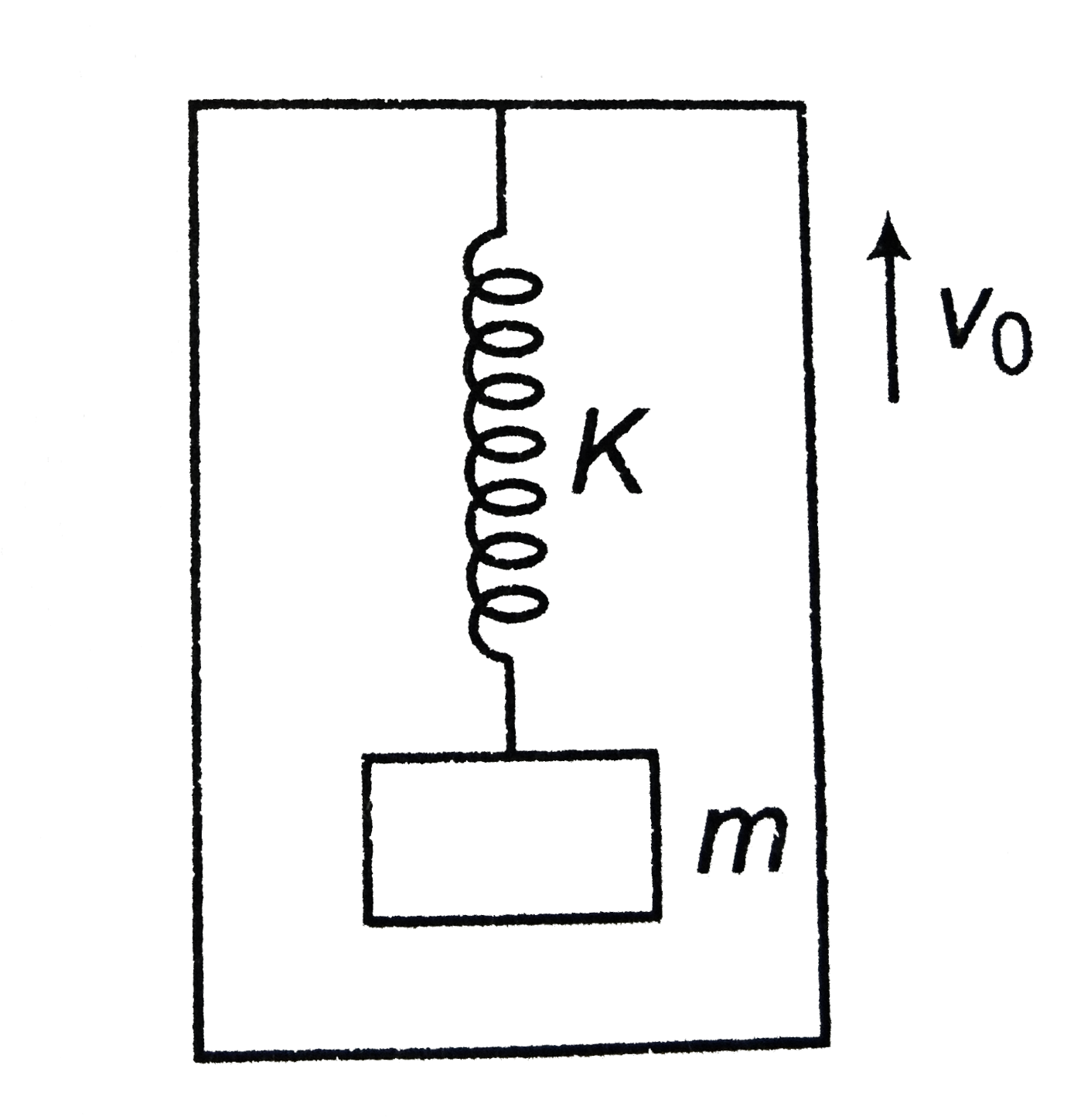
View SolutionA spring block system is kept inside a lift moving with a constant velocity v0 as shown in figure. Block is in equilibrium and at rest with respect to lift. The lift is suddenly stopped at time t=0. Taking upward direction as the positive direction, write x−t equation of the block.
View Solution