A satellite is revolving around a planet in a circular orbit. What will happen, if its speed is increased from υ0 to
(a) √1.5υ0 (b) 2υ0
The correct Answer is:A, B, C
To solve the problem, we need to analyze the effects of increasing the speed of a satellite in a circular orbit around a planet. We will consider two cases: when the speed is increased to √1.5υ0 and when it is increased to 2υ0.
Step 1: Understand the initial conditions
The satellite is initially revolving around a planet in a circular orbit with speed υ0. The gravitational force provides the necessary centripetal force for the satellite's circular motion.
Step 2: Establish the relationship between gravitational force and centripetal force
The gravitational force acting on the satellite is given by:
Fg=GMmr2
where G is the gravitational constant, M is the mass of the planet, m is the mass of the satellite, and r is the radius of the orbit.
The centripetal force required for circular motion is given by:
Fc=mv2r
where v is the speed of the satellite.
Setting these two forces equal gives:
GMmr2=mv2r
We can cancel m from both sides (assuming m≠0) and rearranging gives:
v2=GMr
Thus, the orbital speed υ0 is:
υ0=√GMr
Step 3: Analyze the first case √1.5υ0
Now, if the speed is increased to √1.5υ0:
v=√1.5υ0
The new speed is greater than the original orbital speed.
To find out what happens, we need to determine if this speed is greater than the escape velocity ve. The escape velocity is given by:
ve=√2GMr=√2υ0
Since √1.5≈1.22, we have:
√1.5υ0<√2υ0
This means that the satellite will not escape the gravitational pull of the planet. Instead, it will move into an elliptical orbit.
Step 4: Analyze the second case 2υ0
Now, if the speed is increased to 2υ0:
v=2υ0
We compare this with the escape velocity:
2υ0>√2υ0
Since 2υ0 is greater than the escape velocity, the satellite will have enough kinetic energy to escape the gravitational influence of the planet.
Conclusion
(a) When the speed is increased to √1.5υ0, the satellite will not escape and will move into an elliptical orbit.
(b) When the speed is increased to 2υ0, the satellite will escape the gravitational pull of the planet.
The satellite is initially revolving around a planet in a circular orbit with speed υ0. The gravitational force provides the necessary centripetal force for the satellite's circular motion.
The gravitational force acting on the satellite is given by:
Fg=GMmr2
where G is the gravitational constant, M is the mass of the planet, m is the mass of the satellite, and r is the radius of the orbit.
Fc=mv2r
where v is the speed of the satellite.
GMmr2=mv2r
We can cancel m from both sides (assuming m≠0) and rearranging gives:
v2=GMr
Thus, the orbital speed υ0 is:
υ0=√GMr
Now, if the speed is increased to √1.5υ0:
v=√1.5υ0
The new speed is greater than the original orbital speed.
ve=√2GMr=√2υ0
√1.5υ0<√2υ0
This means that the satellite will not escape the gravitational pull of the planet. Instead, it will move into an elliptical orbit.
Now, if the speed is increased to 2υ0:
v=2υ0
We compare this with the escape velocity:
2υ0>√2υ0
Since 2υ0 is greater than the escape velocity, the satellite will have enough kinetic energy to escape the gravitational influence of the planet.
(a) When the speed is increased to √1.5υ0, the satellite will not escape and will move into an elliptical orbit.
Topper's Solved these Questions
- GRAVITATIONBOOK - DC PANDEY ENGLISHCHAPTER - GRAVITATIONEXERCISE - Level 2 Single Correct
22 Videos
- GRAVITATIONBOOK - DC PANDEY ENGLISHCHAPTER - GRAVITATIONEXERCISE - Level 2 More Than One Correct
10 Videos
- GRAVITATIONBOOK - DC PANDEY ENGLISHCHAPTER - GRAVITATIONEXERCISE - Level 1 Single Correct
27 Videos
- GENERAL PHYSICSBOOK - DC PANDEY ENGLISHCHAPTER - GENERAL PHYSICSEXERCISE - INTEGER_TYPE
2 Videos
- KINEMATICSBOOK - DC PANDEY ENGLISHCHAPTER - KINEMATICSEXERCISE - INTEGER_TYPE
10 Videos
Similar Questions
Knowledge Check
A satellite is moving around the earth with speed v in a circular orbit of radius r. IF the orbit radius is decreased by 1%, its speed will
Aincrease by 1%Bincrease by 0.5 %Cdecrease by 1%Ddecrease by 0.5 %
A satellite is revolving around the earth. Ratio of its orbital speed and escape speed will be.
View SolutionA satellite is revolving around earth in a circular orbit. At some instant the speed of the satellite is increased √2 times its orbital speed keeping its direction unchanged. Then, the new path of the satellite is :
View SolutionA satellite is revolving around earth in a circular orbit at a uniform speed v . If gravitational force suddenly disappears , speed of the satellite will be
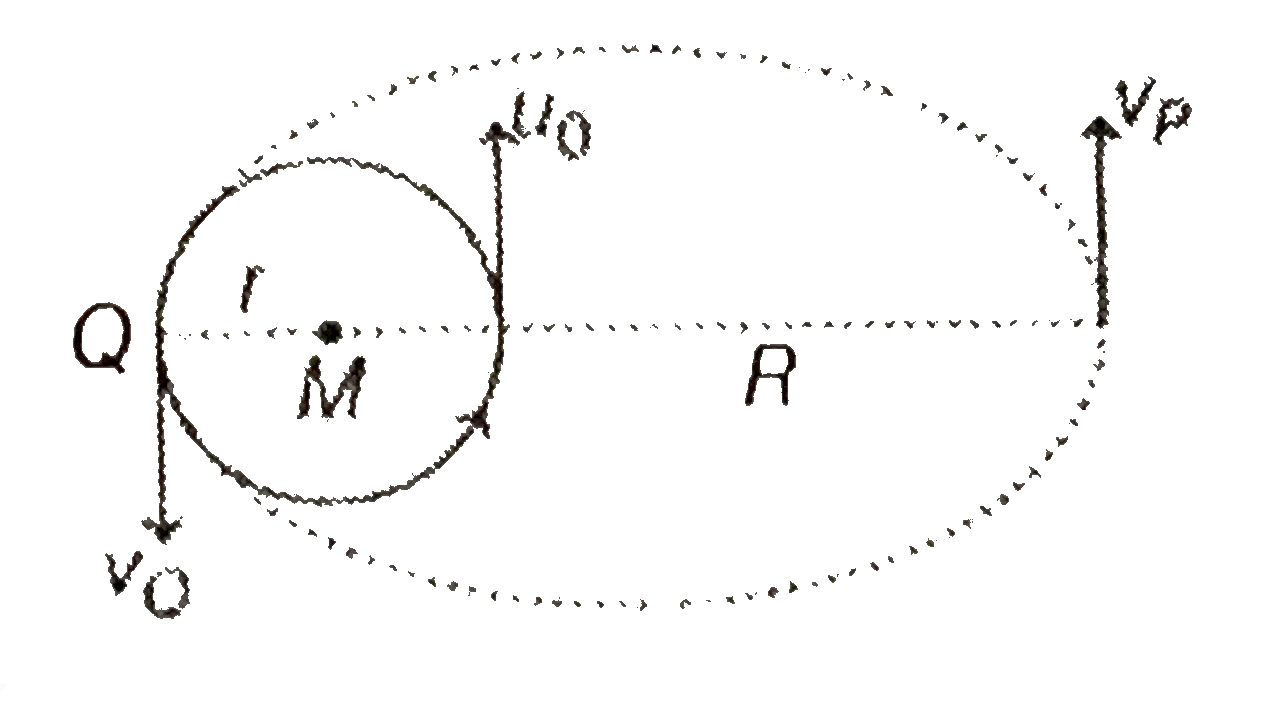
View SolutionA light satellite is initially rotating around a planet in a circular orbit of radius r. Its speed in this circular orbit was u0. It is put in an elliptical orbit by increasing its speed form u0 to vQ ( instantaneously). In the elliptical orbit, the satellite reaches the farthest point P, which is at a distance R from the planet. Satellite's speed at farthest point is vP. At point Q, the speed required by satellite to escape the planet's gravitational pull is vesc
View SolutionA satellite moves around the earth in a circular orbit with speed v. If m is the mass of the satellite, its total energy is
View SolutionA satellite is revolving round the earth in a circular orbit of radius r and velocity υ0. A particle is projected from the satellite in forward direction with realative velocity υ=(√5/4−1)υ0. Calculate its minimum and maximum distances from earth's centre during subsequent motion of the particle.
View SolutionA small satellite revolves around a heavy planet in a circular orbit. At certain point in its orbit a sharp impulse acts on it and instantaneously increases its kinetic energy to 'k' (<2) times without change in its direction of motion show that in its subsequent motion the ratio of its maximum and minimum distance from the planet is k2−k assuming the mass of the satellite is negligibly small as compared to that of the planet.
View Solution
