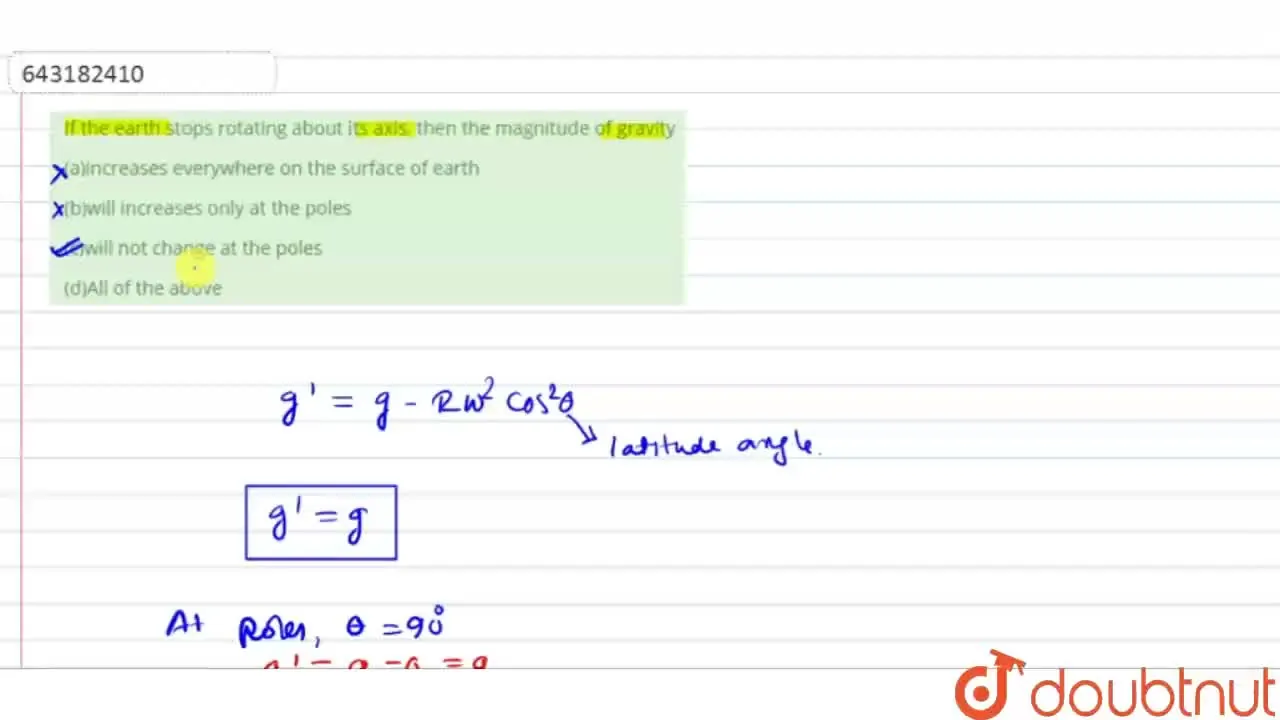
If the earth stops rotating about its axis, then the magnitude of gravity
(a)increases everywhere on the surface of earth
(b)will increases only at the poles
(c)will not change at the poles
(d)All of the above
The correct Answer is:C
At , , independent of .
Related Playlists
- BOOK - DC PANDEY ENGLISHCHAPTER - GRAVITATIONEXERCISE - Level 1 Subjective19videos
GRAVITATION
- BOOK - DC PANDEY ENGLISHCHAPTER - GRAVITATIONEXERCISE - Level 2 Single Correct22videos
GRAVITATION
- BOOK - DC PANDEY ENGLISHCHAPTER - GRAVITATIONEXERCISE - Level 1 Assertion And Reason11videos
GRAVITATION
- BOOK - DC PANDEY ENGLISHCHAPTER - GENERAL PHYSICSEXERCISE - INTEGER_TYPE2videos
GENERAL PHYSICS
- BOOK - DC PANDEY ENGLISHCHAPTER - KINEMATICSEXERCISE - INTEGER_TYPE10videos
KINEMATICS
Similar Questions
Assertion : If the earth stops rotating about its axis, the value of the weight of the body at equator will decrease.
Reason : The centripetal force does not act on the body at the equator.View SolutionStatement I: If the earth suddenly stops rotating about its axis, then the acceleration due to gravity will become the same at all the places.
Statement II: The value of acceleration due to gravity is independent of rotation of the earth.View SolutionOn account of the earth rotating about its axis
View SolutionBy considering earth to be non spherical.
STATEMENT -1 : As one moves from equator to the pole of earth, the value of acceleration due to gravity increases.
and
STATEMENT -2 : If earth stops rotating about its own axis, the value of acceleration due to gravity will be same at pole and at equator.View SolutionSuppose the earth stops rotating about its axis what will be its effect on the weight of a body.
View SolutionShow that if the earth were not rotating about its axis the value of g at the equator would exceed its present value by 3.36cm/s−2. Given the radius of earth =6.371×106m . and angular speed of earth =7.27×10−5rad/s−1
View SolutionA satellite having time period same as that of the earth's rotation about its own axis is orbiting the earth at a height 8R above the surface of earth. Where R is radius of earth. What will be the time period of another satellite at a height 3.5 R from the surface of earth ?
View SolutionLet ω be the angular velocity of the earth's rotation about its axis. Assume that the acceleration due to gravity on the earth's surface has the same value at the equator and the poles. An object weighed at the equator gives the same reading as a reading taken at a depth d below earth's surface at a pole (d<<R). the value of d is-
View SolutionIf the earth stops rotating, the apparent value of g on its surface will
View SolutionIf earth stop spinning about its own axis, what will be the change in acceleration due to gravity on its equator ? The radius of earth is 6.4×106 m and its angular speed is 7.27×10−5rad/s.
View Solution