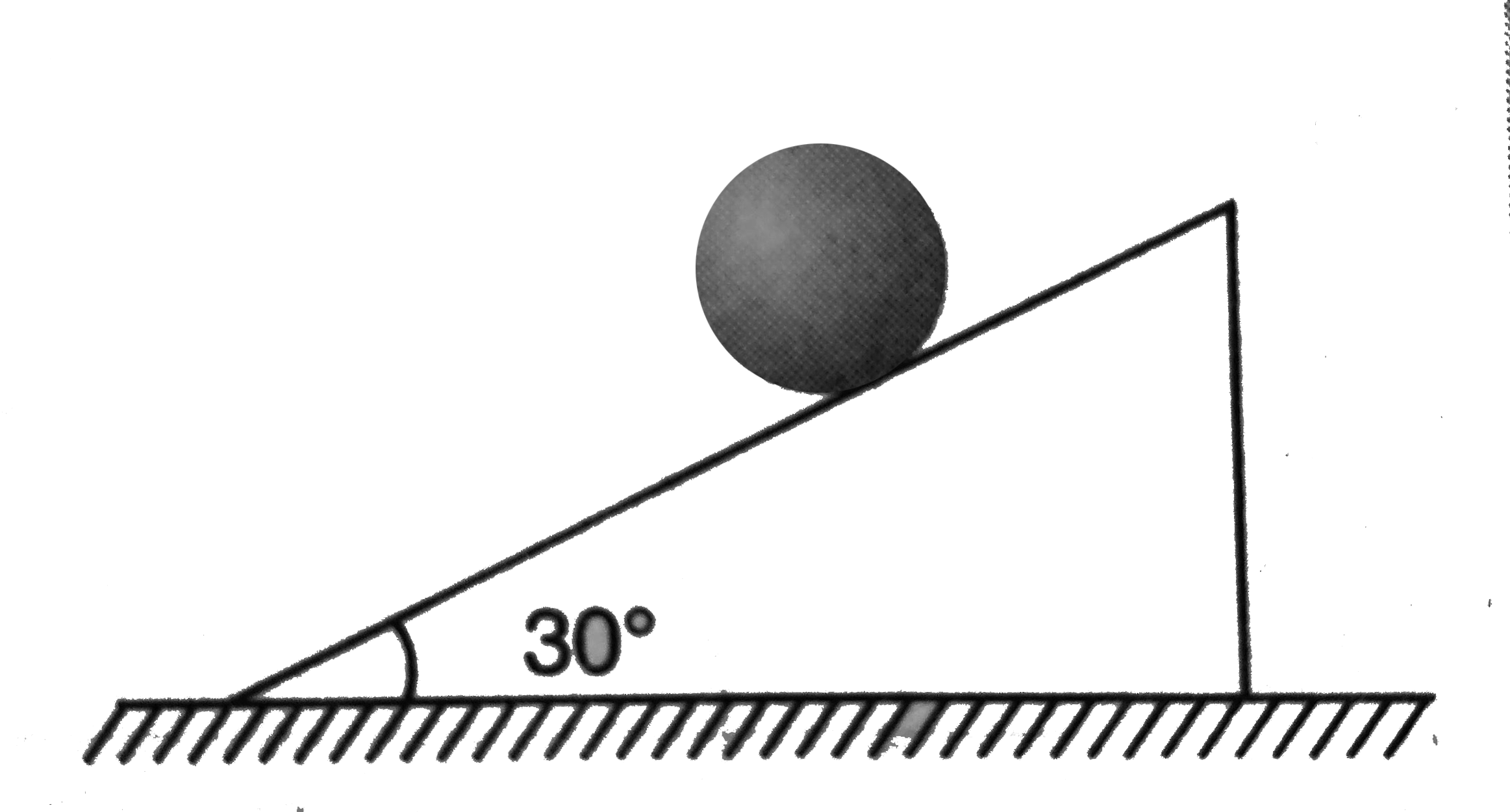
In the figure shown a solid sphere of mass 4kg and radius 0.25 m is placed on a rough surface. (g=10ms2)
(a). Minimum coefficient of friction for pure rolling to take place,
(b). If μ>μmin find linear acceleration of sphere.
(c). if μ=μmin2, find the linear acceleration of cylinder.
Here μmin is the value obtained part (a).
(a). μmin=tanθ1+(mR2/I)
=tan30∘1+5/2=27√3
(b). a=gsinθ1+I/mR2
=(10)sin30∘1+2/5
=257m/s2
(c) a=gsinθ−μgcosθ
=(10)sin30∘−(17√3)(10)(cos30∘)
=5−57=307m/s2
Topper's Solved these Questions
- ROTATIONAL MECHANICSBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONAL MECHANICSEXERCISE - Exercise 12.11
2 Videos
- ROTATIONAL MECHANICSBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONAL MECHANICSEXERCISE - Assertion And Reason
11 Videos
- ROTATIONAL MECHANICSBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONAL MECHANICSEXERCISE - Exercise 12.9
2 Videos
- ROTATIONBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONEXERCISE - (C) Chapter Exercises
39 Videos
- ROTATIONAL MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONAL MOTIONEXERCISE - Integer Type Questions
17 Videos
Similar Questions
A block of mass 10kg is placed on a rough horizontal surface having coefficient of friction μ=0.5 . If a horizontal force of 100N is acting on it, then acceleration of the will be.
View SolutionA block of mass 10kg is placed on a rough horizontal surface having coefficient of friction μ=0.5 . If a horizontal force of 100N is acting on it, then acceleration of the will be.
View Solution
Knowledge Check
A block of mass 10kg is placed on a rough horizontal surface having coefficient of friction μ=0.5 . If a horizontal force of 100N is acting on it, then acceleration of the block will be.
A10ms−2B5ms−2C15ms−2D0.5ms−2
A block of mass 10kg is placed on a rough horizontal surface having coefficient of friction μ=0.5 . If a horizontal force of 100N is acting on it, then acceleration of the block will be.
View Solution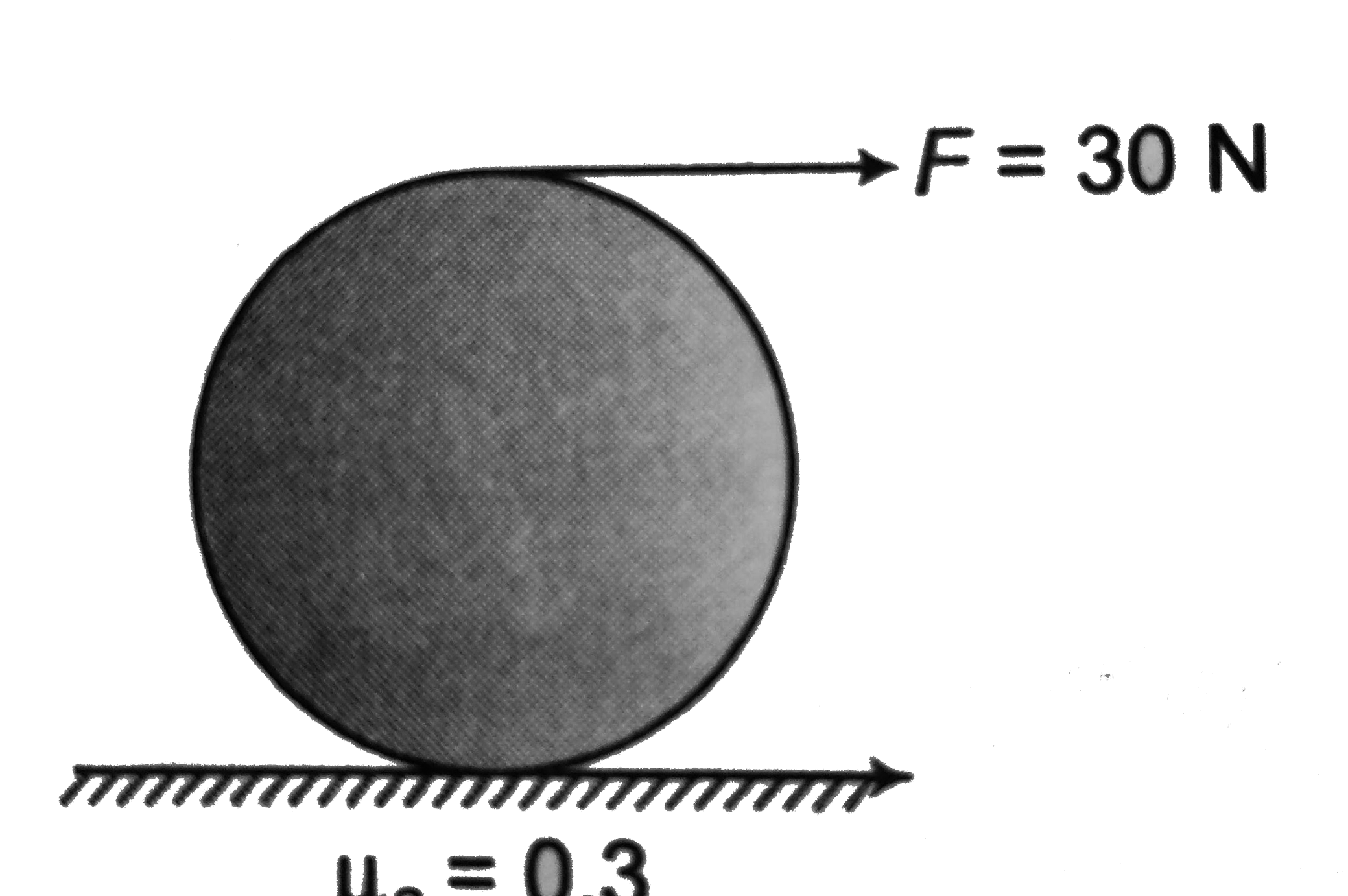
A solid sphere of mass 5 kg and radius 1m is kept over a rough surface as shown in figure. A force F=30N is acting at the topmost point.
(a). Check whether the pure rolling will take place or not
(b). Find direction and magnitude of friction actually acting on the sphere.
(c). Find linear acceleration a and angular acceleration α take g=10m/s2
View SolutionA sphere of mass M and radius R is moving on a rough fixed surface, having coefficient of friction μ. as shown in Fig. It will attain a minimum linear velocity after time (v0>ω0R)

View Solution
A solid sphere of mass 10 kg is placed on a rough surface having coefficient of frictio μ=0.1A constant force F=7N is applied along a line passing through the centre of the sphere as shown in the figure. The value of frictional force on the sphere is
View SolutionA ball of mass M and radius R is released on a rough inclined plane of inclination θ. Friction is not sufficient to prevent slipping. The coefficient friction between the ball and the plane is μ. Find
(a). The linear acceleration of the ball down the plane.
(b). the angular acceleration of the ball about its centre of mass.
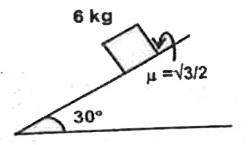
View SolutionA block of mass 6 kg is kept on rough surface as shown in figure. Find acceleration and friction force acting on the block. (Take g=10m/s2)
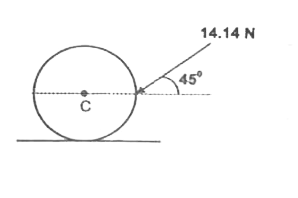
View SolutionA uniform sphere of mass 20kg and radius 10cm is placed on a rough horizontal surface . The coefficient of friction between the sphere and the surface is 0.5.If a force of magnitude 14.14 N is applied on the sphere at an angle of 45∘ with horizontal as shown in the figure, calculate
(a) frictional force
(b) acceleration of the sphere
(c ) angular acceleration of the sphere
View Solution
