A man of mass 60kg jumps from a trolley of mass 20kg standing on smooth surface with absolute velocity 3m/s. Find velocity of trolley and total energy produced by man.
The correct Answer is:A
To solve the problem, we will follow these steps:
Step 1: Understand the System
We have a man with a mass of m1=60kg and a trolley with a mass of m2=20kg. The man jumps off the trolley with an absolute velocity of vm=3m/s. The initial momentum of the system is zero because both the man and the trolley are initially at rest.
Step 2: Apply Conservation of Momentum
Since there are no external forces acting on the system, we can apply the principle of conservation of linear momentum. The initial momentum of the system is given by:
Initial Momentum=0
After the man jumps off, the final momentum of the system can be expressed as:
Final Momentum=m1⋅vm+m2⋅(−vt)
Where vt is the velocity of the trolley (in the opposite direction, hence the negative sign). Setting the initial momentum equal to the final momentum gives us:
0=(60kg)⋅(3m/s)+(20kg)⋅(−vt)
Step 3: Solve for the Velocity of the Trolley
Rearranging the equation to solve for vt:
60⋅3=20⋅vt
180=20⋅vt
vt=18020=9m/s
Thus, the velocity of the trolley is vt=9m/s in the backward direction.
Step 4: Calculate the Kinetic Energy
Next, we need to calculate the total kinetic energy produced by the man after he jumps off. The kinetic energy (KE) is given by the formula:
KE=12mv2
For the man:
KEman=12⋅60kg⋅(3m/s)2=12⋅60⋅9=270J
For the trolley:
KEtrolley=12⋅20kg⋅(9m/s)2=12⋅20⋅81=810J
Step 5: Total Kinetic Energy
Now, we can find the total kinetic energy after the jump:
KEtotal=KEman+KEtrolley=270J+810J=1080J
Step 6: Calculate the Energy Produced by the Man
The energy produced by the man is equal to the change in kinetic energy. Since the initial kinetic energy was zero (both were at rest), the energy produced by the man is:
Energy produced=KEtotal−KEinitial=1080J−0J=1080J
Final Answers
- The velocity of the trolley is 9m/s backward.
- The total energy produced by the man is 1080J.
---
We have a man with a mass of m1=60kg and a trolley with a mass of m2=20kg. The man jumps off the trolley with an absolute velocity of vm=3m/s. The initial momentum of the system is zero because both the man and the trolley are initially at rest.
Since there are no external forces acting on the system, we can apply the principle of conservation of linear momentum. The initial momentum of the system is given by:
Rearranging the equation to solve for vt:
Next, we need to calculate the total kinetic energy produced by the man after he jumps off. The kinetic energy (KE) is given by the formula:
KEman=12⋅60kg⋅(3m/s)2=12⋅60⋅9=270J
KEtrolley=12⋅20kg⋅(9m/s)2=12⋅20⋅81=810J
Now, we can find the total kinetic energy after the jump:
The energy produced by the man is equal to the change in kinetic energy. Since the initial kinetic energy was zero (both were at rest), the energy produced by the man is:
- The velocity of the trolley is 9m/s backward.
- The total energy produced by the man is 1080J.
Topper's Solved these Questions
- CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONBOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONEXERCISE - Exercise 11.4
4 Videos
- CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONBOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONEXERCISE - Exercise 11.5
4 Videos
- CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONBOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONEXERCISE - Exercise 11.2
6 Videos
- CENTRE OF MASS, IMPULSE AND MOMENTUMBOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASS, IMPULSE AND MOMENTUMEXERCISE - Comprehension type questions
15 Videos
- CIRCULAR MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - CIRCULAR MOTIONEXERCISE - Medical entrances s gallery
19 Videos
Similar Questions
A man of mass m=2kg is standing on a platform of mass M=5kg, then at any instant.
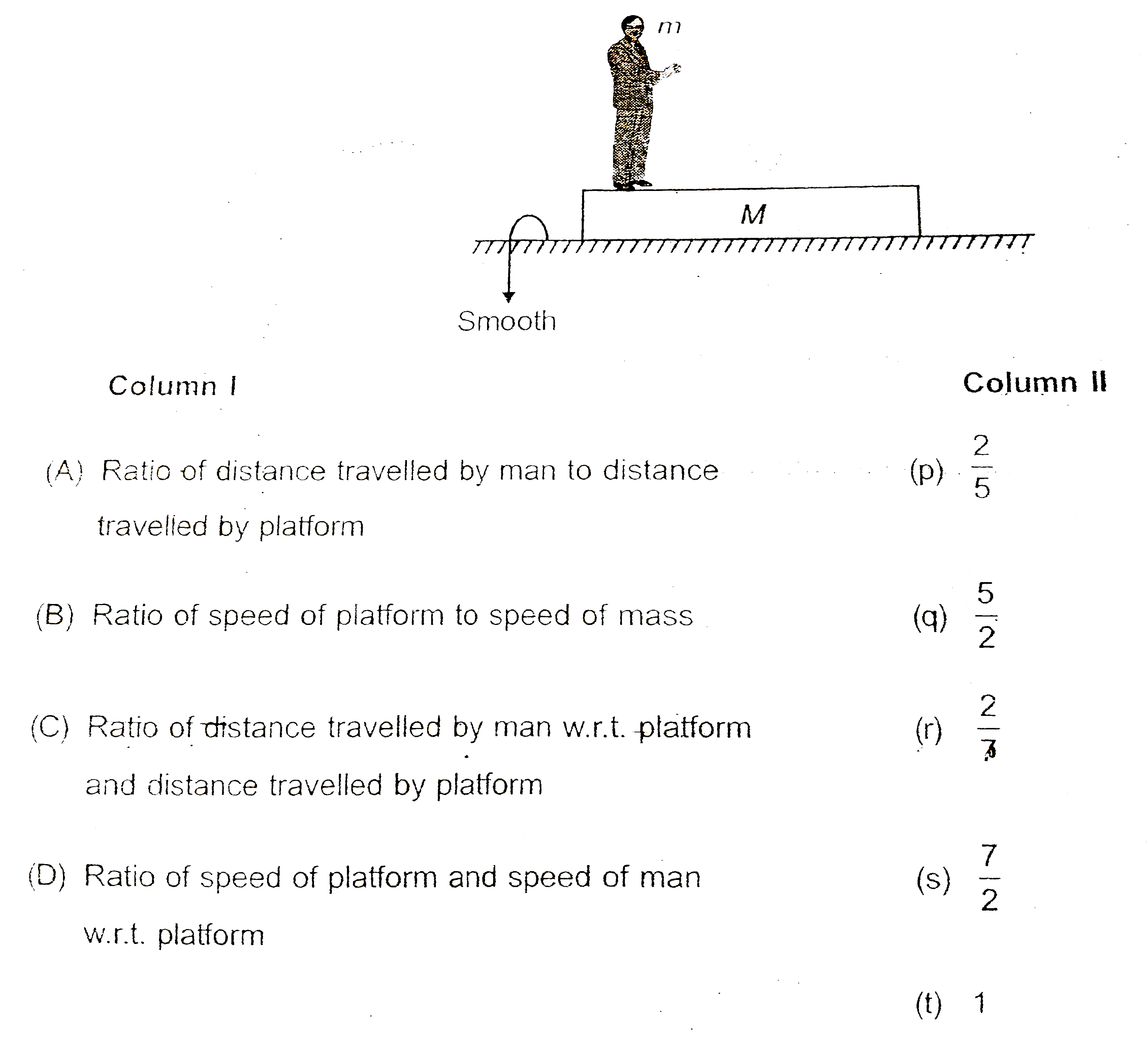
View SolutionA bomb of mass 12 kg explodes into two pieces of masses 4 kg and 8 kg. The velocity of mass 4 kg is 20 m/s. Find the velocity of mass 8 kg.
View SolutionA bomb of mass 12 kg explodes into two piece of masess 4 kg and 8kg . The velocity of mass 4 kg is 20 m/s . Find the velocity of mass 8 kg
View SolutionA girl of mass 25 kg running with a speed of 1.5 m/s jumps on a skateboard of mass 2 kg kept on a smooth surface. What will be their combined velocity?
View SolutionA boy of mass 60kg is standing over a platform of mass 40kg placed over a smooth horizontal surface. He throws a stone of mass 1kg with velocity v=10m/s at an angle of 45∘ with respect to the ground. Find the displacement of the platform (with boy) on the horizontal surface when the stone lands on the ground. Take g=10m/s2.
View SolutionA boy of mass 60kg is standing over a platform of mass 40kg placed over a smooth horizontal surface. He throws a stone of mass 1kg with velocity v=10m/s at an angle of 45∘ with respect to the ground. Find the displacement of the platform (with boy) on the horizontal surface when the stone lands on the ground. Take g=10m/s2.
View SolutionA girl having mass of 35 kg sits on a trolley of mass 5 kg. The trolley is given an initial velocity of 4m//s by applying a force. The trolley comes to rest after travelling a distance of 16m. (a) How much work is done on the trolley ? (b) How much work is done by the girl ?
View SolutionA girl of mass 25 kg running with a speed of 1⋅5ms jumps on a skateboard of mass 2 kg kept on a surface . What will be their combined velocity ?
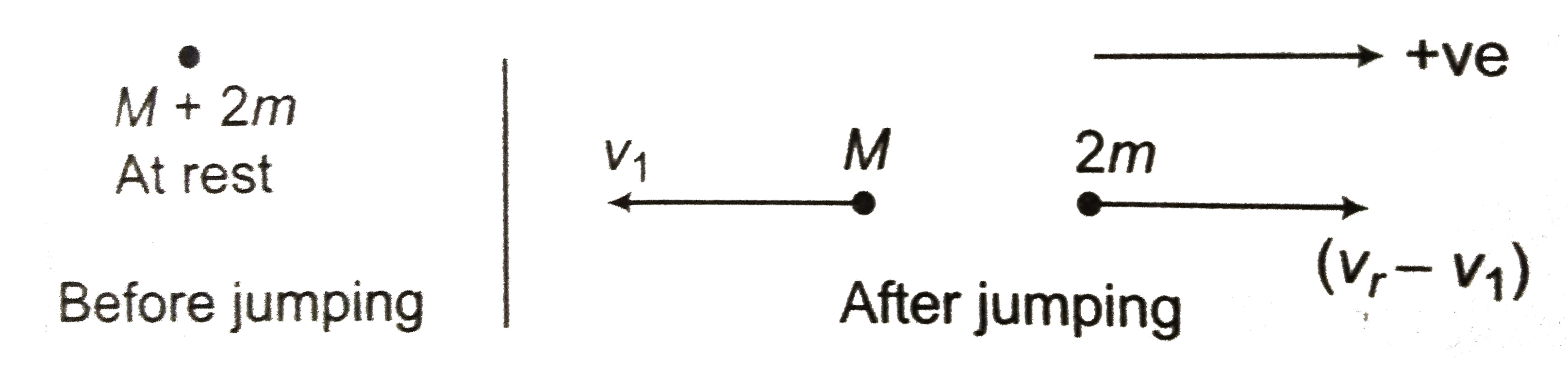
View SolutionA trolley of mass M is at rest over a smooth horizontal surface as shown in figure. Two boys each of mass 'm' are standing over the trolley. They jump from the trolley (towards right) with relative velocity vr [relative to velocity of trolley just after jumping]
(a) together
(b) one after the other.
Find velocity of trolley in both cases.
View SolutionA wooden plank of mass 20kg is resting on a smooth horizontal floor. A man of mass 60kg starts moving from one end of the plank to the other end. The length of the plank is 10m. Find the displacement of the plank over the floor when the man reaches the other end of the plank.

View Solution
