A vertical frictionless semicircular track of radius 1m fixed on the edge og a movable trolley (figure). Initially, the system is rest and a mass m is kept at the top of the track. The trolly starts moving to the right with a uniform horizontal acceleration a=2g/9 . The mass slides down the track, eventually losing contact with it and dropping to the floor 1.3m below the trolly. This 1.3m is from the point where mass loses contact. (g=10m/s2)
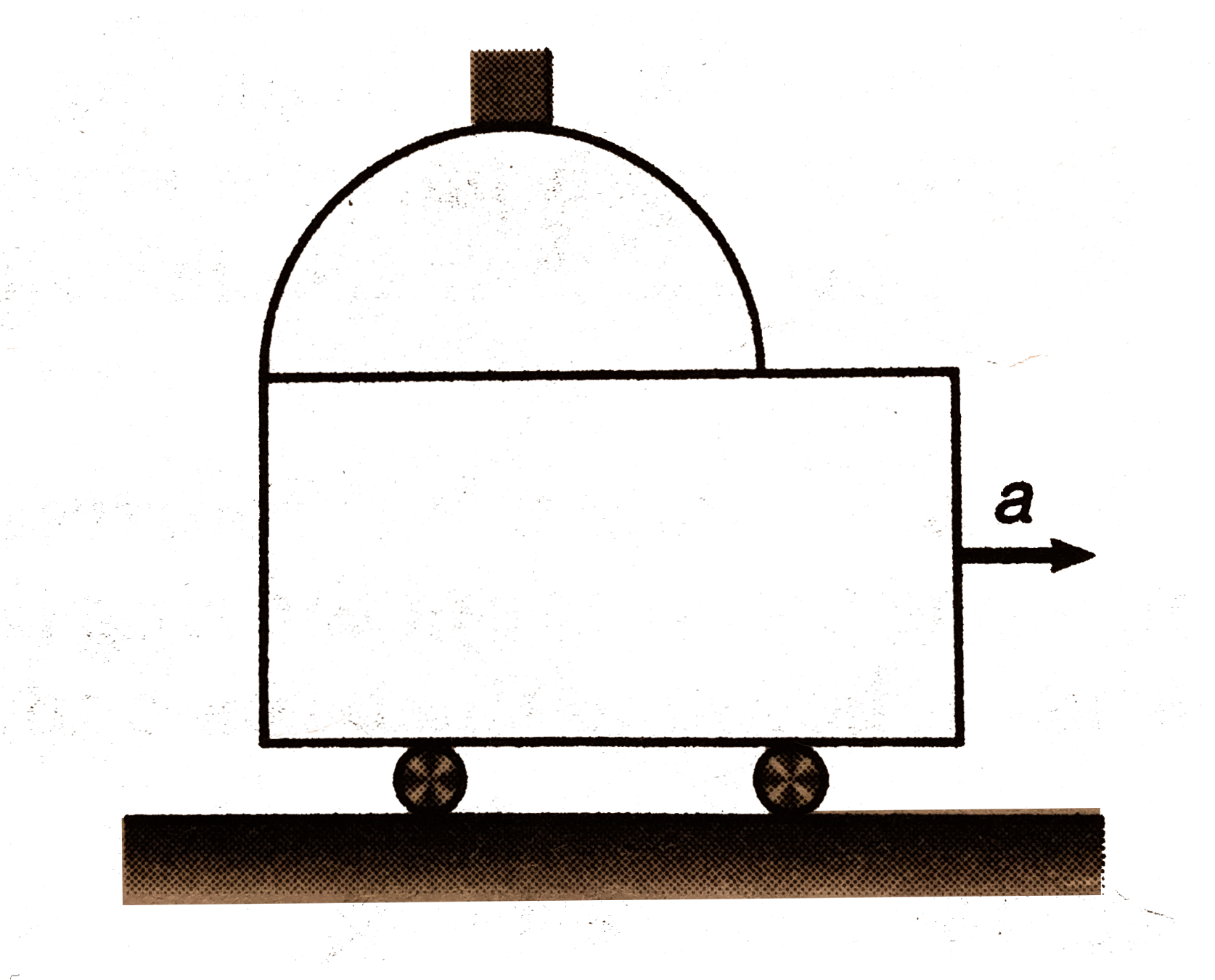
(a) Calculate the angle θ at which it loses contact with the trolly and
(b) the time taken by the mass to drop on the floor, after losing contact.
The correct Answer is:B, C
(a) Let vr be the velocity of mass relative to track at angular position θ .
From work energy theorem, KE of particle relative to track
=Work done by force of gravity+work done by pseudo force
:. 12mv2r=mg(1−cosθ)+m(2g9)sinθ
opr v2=2g(1−cosθ)+4g9sinθr
Particle leaves contact with the track where N=0

or mgcosθ−m(2g9)sinθ=mv2r
or gcosθ−2g9sinθ=2g(1−cosθ)+4g9sinθ
or 3cosθ−69sinθ2
Solving this, we get θ≈37∘
(b) From Eq. (i) we have,
vr=√2g(1−cosθ)+4g9sinθ
or vr=2.58m/satθ=37∘
Vertical component of its velocity is
vy=vrsinθ
=2.58×35
=1.55m/s
Now, 1.3=1.55t+5t2(∵s=ut+12>2)
or 5t2+1.55t−1.3=0
or t=0.38s
Topper's Solved these Questions
- CIRCULAR MOTIONBook:DC PANDEY ENGLISHChapter:CIRCULAR MOTIONExercise:JEE Main
Explore 23 Videos
- CIRCULAR MOTIONBook:DC PANDEY ENGLISHChapter:CIRCULAR MOTIONExercise:JEE Advanced
Explore 24 Videos
- CIRCULAR MOTIONBook:DC PANDEY ENGLISHChapter:CIRCULAR MOTIONExercise:Level 2 Subjective
Explore 13 Videos
- CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONBook:DC PANDEY ENGLISHChapter:CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONExercise:Level 2 Subjective
Explore 21 Videos
- COMMUNICATION SYSTEMBook:DC PANDEY ENGLISHChapter:COMMUNICATION SYSTEMExercise:Only One Option is Correct
Explore 27 Videos
Similar Questions
A person moves on a semicircular track of radius 40 m. If he starts at one end of the track and reaches the other end, find the distance covered and magnitude of displacement of the person.
View SolutionA car of mass 1000 kg moves on a circular track of radius 100 m with a speed of 40 m/s. Calculate the magnitude of its angular momentum relative to the centre of the track.
View SolutionA train of mass M is moving on a circular track of radius R with constant speed v. The length of the train is half of the perimeter of the track. The linear momentum of the train will be
View SolutionA train of mass M is moving on a circular track of radius R with constant speed v. The length of the train is half of the perimeter of the track. The linear momentum of the train will be
View SolutionA particle of mass m starts to slide down from the top of the fixed smooth sphere. What is the tangential acceleration when it break off the sphere ?
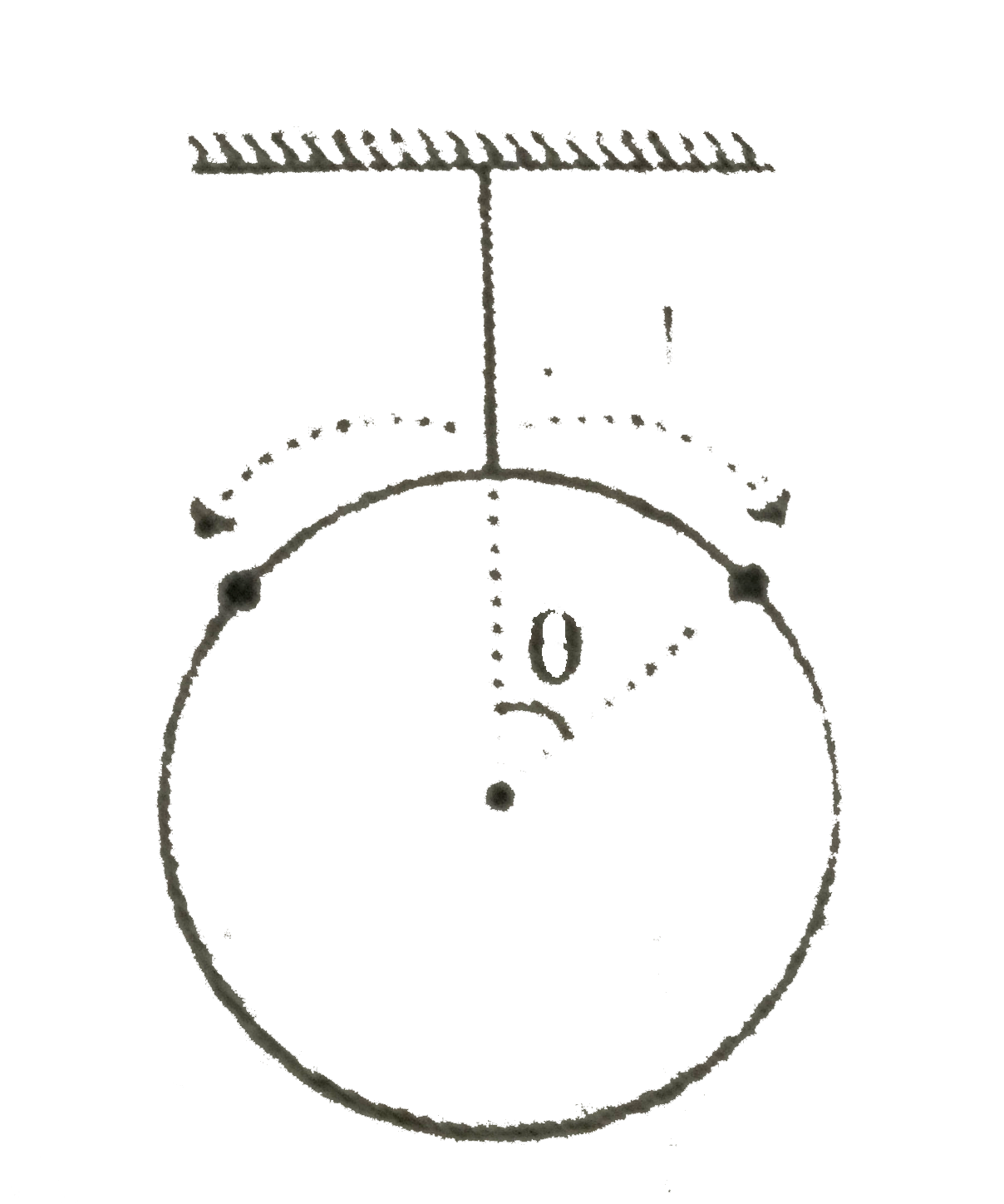
View SolutionA smooth circular track of mass M is vertically hung by a string down the ceiling. Two small rings, each of mass m, are initially at rest at the top of the track. They then slide down simultaneously along the track in opposite directions. Find the position of the rings when the tension in the string is zero.
View SolutionA block of mass M with a semi - circular track of radius R rests on a smooth floor. A sphere of mass m and radius r is released from rest from A. Find the velocity of sphere and track , when the sphere reaches B.

View SolutionA block of mass m slides down a smooth vertical circular track. During the motion, the block is in
View SolutionAOB is a smooth semicircular track of radius r. A block of mass m is given a velocity √2rg parallel to track at point A. Calculate normal reaction between block and track when block reaches at point O.

View SolutionA block of mass m1 rests on a horizontal table. A string tied to the block is passed on a frictionless pulley fixed at the end of the table and to the other end of string is hung another block of mass m2. The acceleration of the system is
View Solution