A helicopter lifts a 72kg astronaut 15m vertically from the ocean by means of a cable. The acceleration of the astronaut is g10. How much work is done on the astronaut by (g=9.8m/s2)
(a) what is the kinetic energy of the block as it passese through x=2.0m?<br>(b)Wˆisthemaxiμmk∈etice≠rgyoftheblockbetweenx=0 and x=2.0m?
The correct Answer is:A, B, C, D
To solve the problem step by step, we need to calculate the work done on the astronaut by the helicopter and then find the kinetic energy at different points.
Step 1: Calculate the gravitational force acting on the astronaut.
The gravitational force (weight) acting on the astronaut can be calculated using the formula:
Fg=m⋅g
Where:
- m=72kg (mass of the astronaut)
- g=9.8m/s2 (acceleration due to gravity)
Calculating this gives:
Fg=72kg⋅9.8m/s2=705.6N
Step 2: Determine the net force acting on the astronaut.
The astronaut is accelerating upwards with an acceleration of g10:
a=g10=9.8m/s210=0.98m/s2
Using Newton's second law, we can find the net force:
Fnet=m⋅a=72kg⋅0.98m/s2=70.56N
Step 3: Calculate the tension in the cable.
The tension T in the cable can be calculated by balancing the forces acting on the astronaut:
T−Fg=Fnet
Thus,
T=Fg+Fnet
Substituting the values:
T=705.6N+70.56N=776.16N
Step 4: Calculate the work done on the astronaut.
The work done W by the tension force as the astronaut is lifted a distance S=15m is given by:
W=T⋅S
Substituting the values:
W=776.16N⋅15m=11642.4J
Step 5: Kinetic energy at x=2.0m.
To find the kinetic energy KE at x=2.0m, we can use the work-energy principle. The work done on the astronaut from x=0 to x=2.0m will equal the change in kinetic energy:
KE=Wnet=T⋅x−Fg⋅x
Where x=2.0m:
KE=(776.16N⋅2.0m)−(705.6N⋅2.0m)
Calculating this gives:
KE=(1552.32J)−(1411.2J)=141.12J
Step 6: Maximum kinetic energy between x=0 and x=2.0m.
The maximum kinetic energy will occur at the end of the interval, which is at x=2.0m. Thus, the maximum kinetic energy is the same as calculated above:
KEmax=141.12J
Final Answers:
(a) The kinetic energy of the astronaut as it passes through x=2.0m is 141.12J.
(b) The maximum kinetic energy of the astronaut between x=0 and x=2.0m is also 141.12J.
The gravitational force (weight) acting on the astronaut can be calculated using the formula:
Fg=m⋅g
Where:
- m=72kg (mass of the astronaut)
- g=9.8m/s2 (acceleration due to gravity)
Fg=72kg⋅9.8m/s2=705.6N
The astronaut is accelerating upwards with an acceleration of g10:
a=g10=9.8m/s210=0.98m/s2
Fnet=m⋅a=72kg⋅0.98m/s2=70.56N
The tension T in the cable can be calculated by balancing the forces acting on the astronaut:
T−Fg=Fnet
Thus,
T=Fg+Fnet
Substituting the values:
T=705.6N+70.56N=776.16N
The work done W by the tension force as the astronaut is lifted a distance S=15m is given by:
W=T⋅S
Substituting the values:
W=776.16N⋅15m=11642.4J
To find the kinetic energy KE at x=2.0m, we can use the work-energy principle. The work done on the astronaut from x=0 to x=2.0m will equal the change in kinetic energy:
KE=Wnet=T⋅x−Fg⋅x
Where x=2.0m:
KE=(776.16N⋅2.0m)−(705.6N⋅2.0m)
Calculating this gives:
KE=(1552.32J)−(1411.2J)=141.12J
The maximum kinetic energy will occur at the end of the interval, which is at x=2.0m. Thus, the maximum kinetic energy is the same as calculated above:
KEmax=141.12J
(a) The kinetic energy of the astronaut as it passes through x=2.0m is 141.12J.
Topper's Solved these Questions
- WORK, ENERGY & POWERBOOK - DC PANDEY ENGLISHCHAPTER - WORK, ENERGY & POWEREXERCISE - Level 2 Objective
30 Videos
- WORK, ENERGY & POWERBOOK - DC PANDEY ENGLISHCHAPTER - WORK, ENERGY & POWEREXERCISE - Level 2 More Than One Correct
9 Videos
- WORK, ENERGY & POWERBOOK - DC PANDEY ENGLISHCHAPTER - WORK, ENERGY & POWEREXERCISE - Level 1 Objective
38 Videos
- WAVE MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - WAVE MOTIONEXERCISE - Integer Type Question
11 Videos
- WORK, ENERGY AND POWERBOOK - DC PANDEY ENGLISHCHAPTER - WORK, ENERGY AND POWEREXERCISE - MEDICAL ENTRACES GALLERY
33 Videos
Similar Questions
What is the kinetic energy of a baseball (mass=0.15kg) moving with a speed of 20 m/s?
View SolutionFigure shows, a 3.5kg block accelerated by a compressed spring whose spring constant is 740N/m. After, leaving the spring at the spring' s relaxed length, the block travels over a horizontal surfce, with a coefficient of kinetic friction of 0.25, for a distance of 7.8m before stopping. (g=9.8m/s2).
(a) What is the increase in the thermal energy of the block-floor system ?
(b) What is the maximum kinetic energy of the block ?
(c) Through what distance is the spring compressed before the block begins to move ?
 .
.
View SolutionThe only force acting on a 2.0−kg body as it moves along the x-axis varies as shown in figure. The velocity of the body at x=0 is 4.0ms−1.

a. What is the kinetic energy of the body at x=3.0m?
b. At what value of x will the body have a kinetic energy of 8.0J?
c. What is the maximum kinetic energy attained by the body between x=0 and x=5.0m?
View SolutionIf coeffiecient of friction between the block of mass 2kg and table is 0.4 then out acceleration of the system and tension in the string. (g=10m/s2)
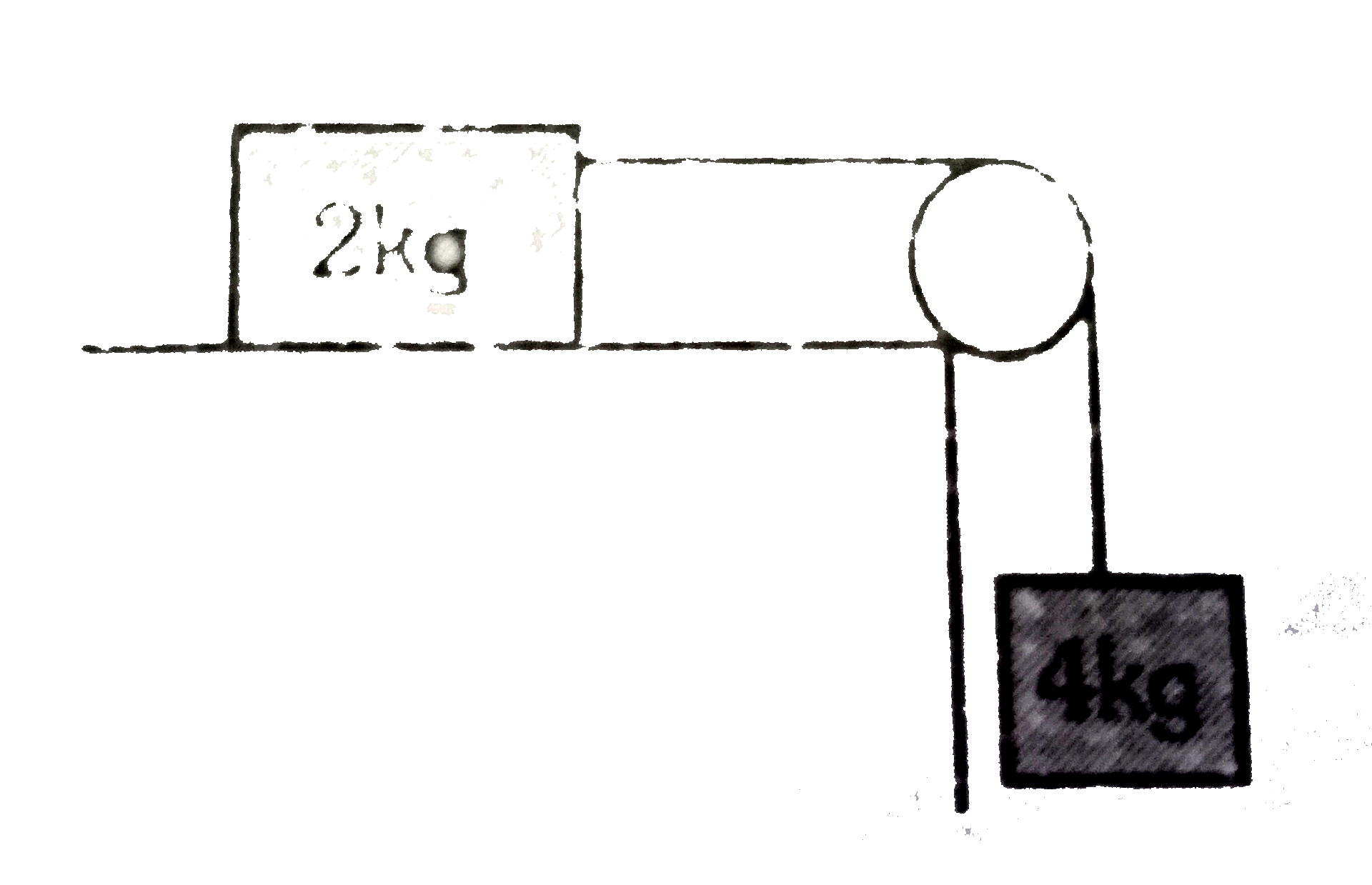
View SolutionThe graph below shows how the force on a mass depends on the position of the mass. What is the change in the kinetic energy of the mass as it moves from x=0.0m to x=3.0 m ?

View SolutionA man pulls out a block of mass m from the depth d with help of a light string. If acceleration of the block is g2 then the work done by the string on the block will be
View SolutionA 1.5−kg block is initially at rest on a horizontal frictionless surface when a horizontal force in the positive direction of x-axis is applied to the block. The force is given by →F=(4−x2)→iN, where x is in meter and the initial position of the block is x=0.
The maximum kinetic energy of the block between x=0 and x=2.0m is
A.2.33 J B.8.67 J C.5.33 J D.6.67 J
View SolutionA block rides on position that is moving vertically with simple harmonic motion. The maximum speed of the piston is 2m/s. At what amplitude of motion will the block and piston separate? (g=10m/s2)
View SolutionA 1.5 kg block is initially at rest on a horizontal frictionless surface when a horizontal force in the positive direction of an axis is applied to the block. The force is given by →F=(1−x2)ˆiN, where x is in meters and the initial position of the block is x=0 the maximum kinetic energy of the block is 2nJ in between x=0 ad x=2m find the value of n.
View SolutionA 4.00g bullet travelling horizontally with a velocity of magnitude 500m/s is fired into a wooden block with a mass of 1.00kg, initially at rest on a level surface. The bullet passes through the block and emerges with speed 100m/s. The block slides a distance of 0.30m along the surface from its initial position.
(a) What is the coefficient of kinetic friction between block and surface?
(b) What is the decrease in kinetic energy of the bullet?
(c) What is the kinetic energy of the block at the instant after the bullet has passed through it? Neglect friction during collision of bullet with the block.
View Solution
