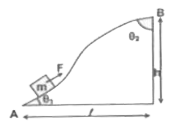
A body of mass m was slowly hauled up the hill as shown in the fig. by a force F which at each point was directed along a tangent to the trajectory. Find the work performed by this force, if the height of the hill is h, the length of its base is I and the coefficient ot friction is μ.
.
Four forces are acting on the body:
1. weight (mg)
2. normal reaction (N)
3. friction (f) and
4. the applied force (F). Using work-energy theorem
Wnet=ΔKE
or Wmg+WN+Wf+Wf=…….(i)
Here, ΔKE=0, because Ki=0Kf
Wmg=−mgh
WN=0
(as normal reaction is perpendicular to displacement at all points)
Wf can be calculated as under
f=μmgcosθ
∴(dWAB)f=−fds
=−(μmgcosθ)ds
=−μmg(dl) , (as dscosθ=dl)
∴f=−μmg∑dl=−μmgl
Substituting these values in Eq. (i), we get
WF=mgh+μmgl
Topper's Solved these Questions
- BOOK - DC PANDEY ENGLISHCHAPTER - WORK, ENERGY & POWEREXERCISE - Solved Examples12videos
WORK, ENERGY & POWER
- BOOK - DC PANDEY ENGLISHCHAPTER - WORK, ENERGY & POWEREXERCISE - TYPE21videos
WORK, ENERGY & POWER
- BOOK - DC PANDEY ENGLISHCHAPTER - WAVE MOTIONEXERCISE - Integer Type Question11videos
WAVE MOTION
- BOOK - DC PANDEY ENGLISHCHAPTER - WORK, ENERGY AND POWEREXERCISE - MEDICAL ENTRACES GALLERY33videos
WORK, ENERGY AND POWER
Similar Questions
A body of mass m was slowly pulled up the hill by a force F which at each point was directed along the tangent of the trajectory. All surfaces aresmooth. Find the work performed by this force.
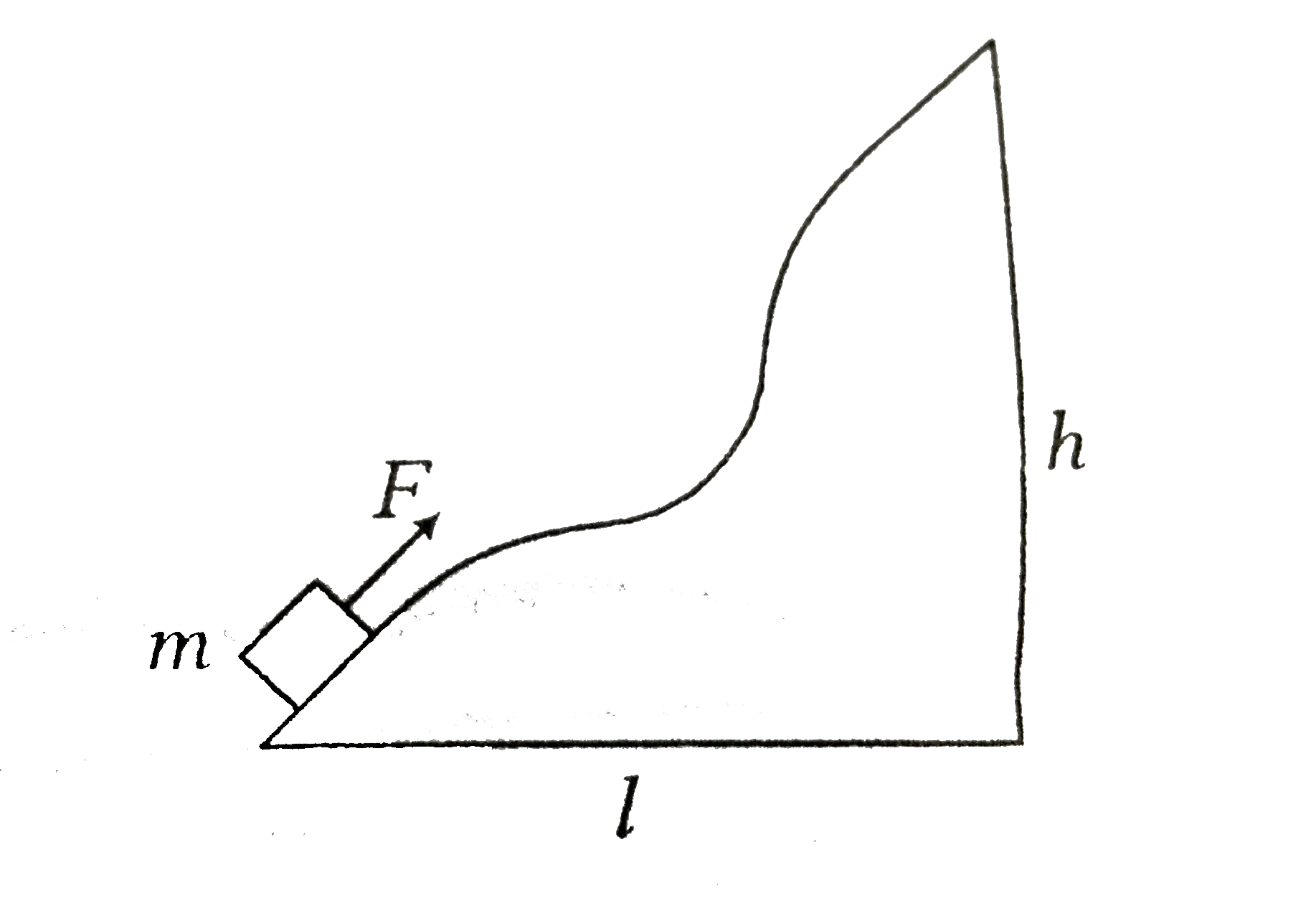View SolutionA body of mass m was slowly pulled up the hill by a force F which at each point was directed along the tangent of the trajectory. All surfaces are smooth. Find the work done by this force
View SolutionA body of mass M was slowly hauled up a rough hill by a force F which at each point was directed along a tangent to the hill. Work done by the force
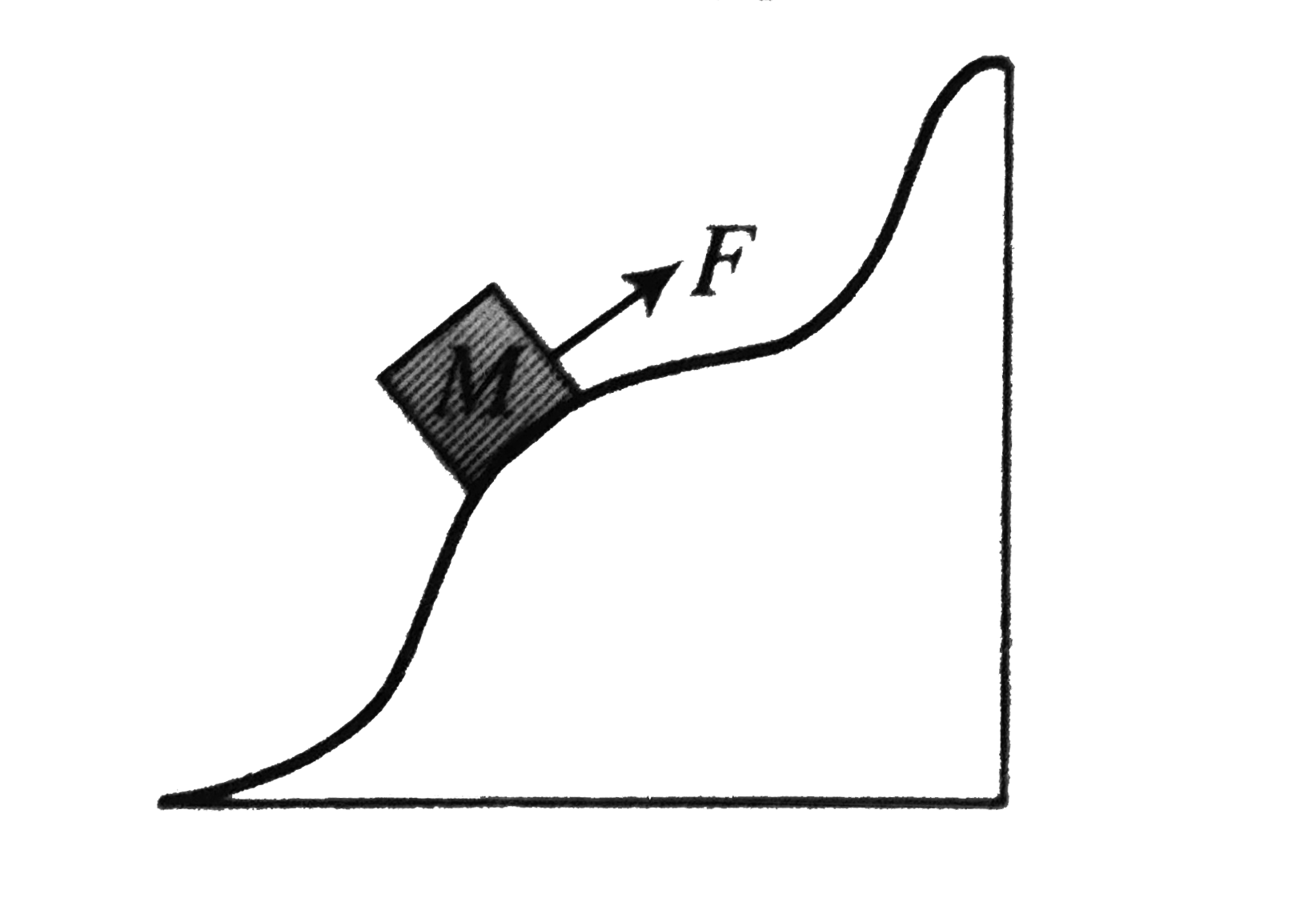View SolutionAn object of mass m is tied to a string of length l and a variable force F is applied on it which brings the string gradually at angle θ with the vertical. Find the work done by the force F
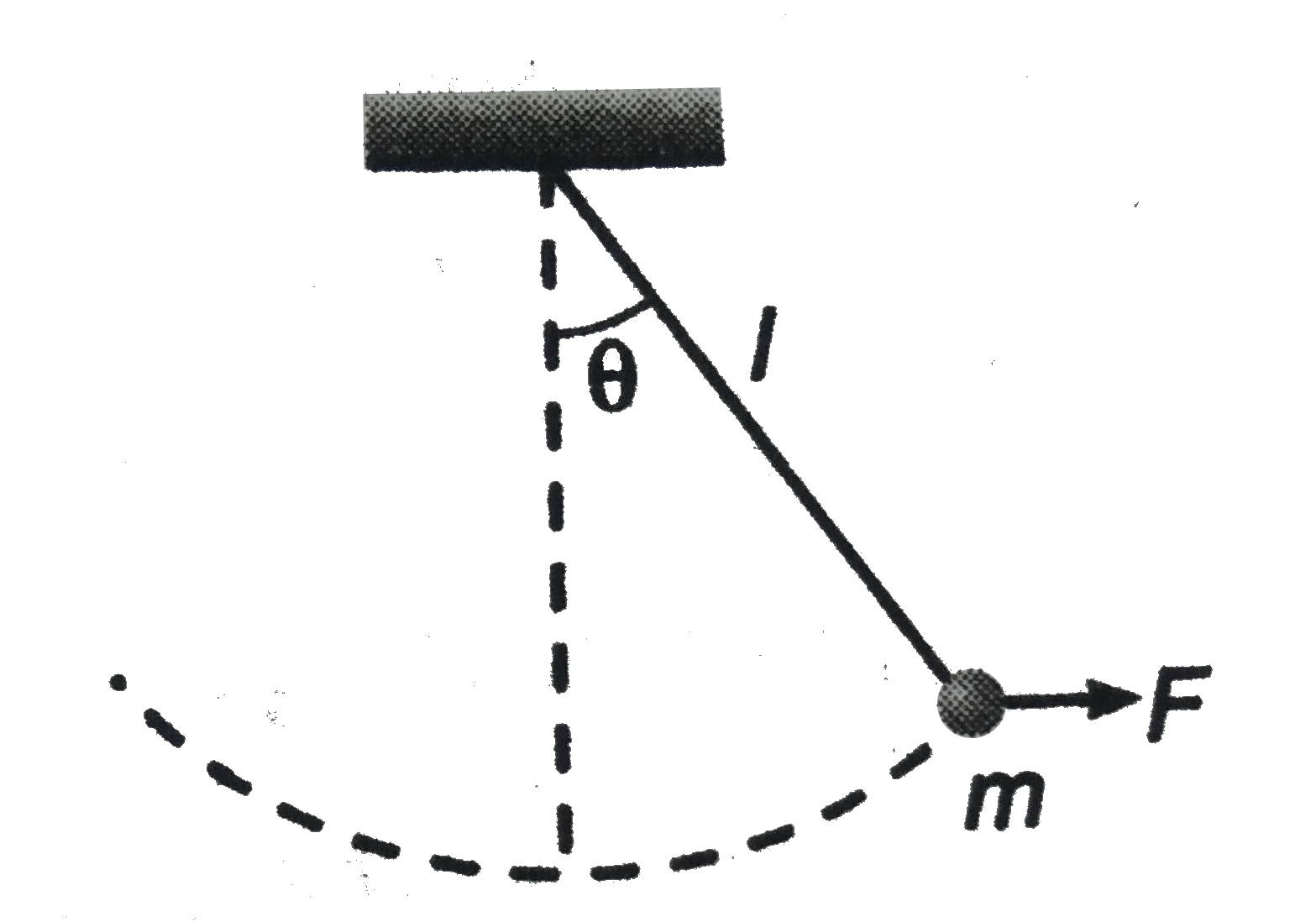. View SolutionA small block of mass m os takes slowly up a fixed hemisphere from P to Q and then slowly down along its surface from Q to S by force F, which at each point of the surface, is tangential to the surface. If the coefficient of friction is μ, then the work performed by the force F in taking the block from P to S along the hemispherical surface of radius R is :
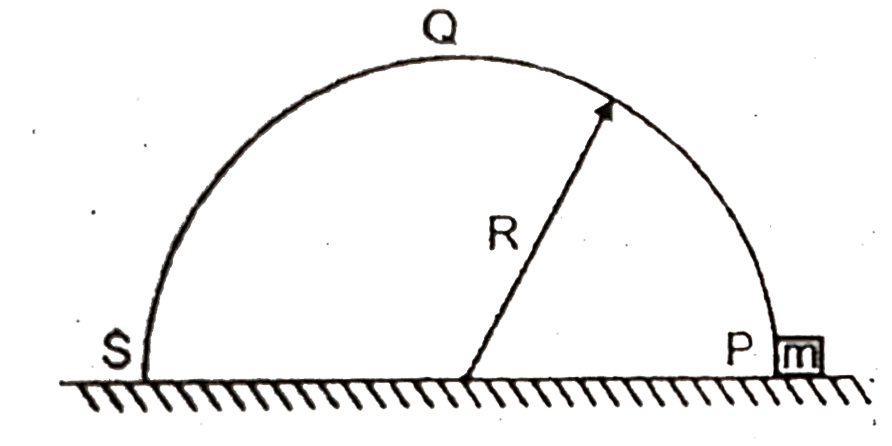View SolutionAn object of mass m is tied to a string of length l and a variable force F is applied on it which brings the string gradually at angle thit θ with the vertical. Find the work done by the force F
. View SolutionA small object of mass 'm' is moved over a rough, curved surface as shown. The force which moves it along the dotted path shown is always tangential to the curved path. If the object moves with negligible speed, find the work done by the force F in moving it from A to B. The coefficient of friction between the object and the curved surface is μ.
View SolutionA block of mass m is slowly carried on a inclined plane by a force F which always acts along the tangent to the plane. If the co-efficient of friction between the block and incline be μ, then work done by force of friction while carrying block from bottom of the plane to the top will be :
A. dependent on the actual shape of the path between point A and B.
B. will have a total positive value
C. will not change if force F is not applied along the tangent to the plane always.
D. independent of the actual shape of the path between points A and B.View SolutionA body of mass m is moved up (slowly) the plane of verying slope by a tangential force upto height h. The coefficient of friction between the surface and the block is μ.
Select correct option(s)View SolutionA body of mass m is moved up (slowly) the plane of verying slope by a tangential force upto height h. The coefficient of friction between the surface and the block is μ.
Select correct option(s)View Solution