A 30kg mass is intially at rest on floor of a truck . The coefficient of static friction between the mass and the floor of truck in 0.3 and coefficient of kinetic friction is 0.2 . Intially the truck is travelling due east at constant speed.Find the magnitude and direction of the friction force acting on the mass , if : (take g=10m/s2)
(a) the truck acdceleration at 1.8m/s2 eastward
(b) the truck acdceleration at 3.8m/s2 westward
To solve the problem, we need to analyze the two scenarios given:
1. When the truck accelerates eastward at 1.8m/s2.
2. When the truck accelerates westward at 3.8m/s2.
Given Data:
- Mass (m) = 30kg
- Coefficient of static friction (μs) = 0.3
- Coefficient of kinetic friction (μk) = 0.2
- Gravitational acceleration (g) = 10m/s2
1. Calculate the required frictional force:
Frequired=m⋅a=30kg⋅1.8m/s2=54N
2. Calculate the maximum static friction force:
Fmax static=μs⋅N=μs⋅(m⋅g)=0.3⋅(30kg⋅10m/s2)=90N
3. Determine if the mass will remain at rest:
Since 54N<90N, the static friction is sufficient to keep the mass at rest. Therefore, the friction force acting on the mass is equal to the required friction force:
Ffriction=54N(eastward)
(b) Truck acceleration at 3.8m/s2 westward
1. Calculate the required frictional force:
Frequired=m⋅a=30kg⋅3.8m/s2=114N
2. Calculate the maximum static friction force (same as before):
Fmax static=90N
3. Determine if the mass will remain at rest:
Since 114N>90N, the static friction is not sufficient to keep the mass at rest. The mass will start moving, and we need to use kinetic friction.
4. Calculate the kinetic friction force:
Fkinetic=μk⋅N=μk⋅(m⋅g)=0.2⋅(30kg⋅10m/s2)=60N
5. Calculate the net force acting on the mass:
The net force acting on the mass in the westward direction is:
Fnet=Frequired−Fkinetic=114N−60N=54N(westward)
6. Calculate the acceleration of the mass:
Using Newton's second law:
Fnet=m⋅a⟹a=Fnetm=54N30kg=1.8m/s2(westward)
Summary of Results:
- (a) The friction force acting on the mass when the truck accelerates eastward at 1.8m/s2 is 54N (eastward).
- (b) The friction force acting on the mass when the truck accelerates westward at 3.8m/s2 is 60N (opposing the direction of motion, which is eastward).
2. When the truck accelerates westward at 3.8m/s2.
- Mass (m) = 30kg
- Coefficient of static friction (μs) = 0.3
- Coefficient of kinetic friction (μk) = 0.2
- Gravitational acceleration (g) = 10m/s2
Frequired=m⋅a=30kg⋅1.8m/s2=54N
Fmax static=μs⋅N=μs⋅(m⋅g)=0.3⋅(30kg⋅10m/s2)=90N
Since 54N<90N, the static friction is sufficient to keep the mass at rest. Therefore, the friction force acting on the mass is equal to the required friction force:
Ffriction=54N(eastward)
Frequired=m⋅a=30kg⋅3.8m/s2=114N
Fmax static=90N
Since 114N>90N, the static friction is not sufficient to keep the mass at rest. The mass will start moving, and we need to use kinetic friction.
Fkinetic=μk⋅N=μk⋅(m⋅g)=0.2⋅(30kg⋅10m/s2)=60N
The net force acting on the mass in the westward direction is:
Fnet=Frequired−Fkinetic=114N−60N=54N(westward)
Using Newton's second law:
Fnet=m⋅a⟹a=Fnetm=54N30kg=1.8m/s2(westward)
- (a) The friction force acting on the mass when the truck accelerates eastward at 1.8m/s2 is 54N (eastward).
- (b) The friction force acting on the mass when the truck accelerates westward at 3.8m/s2 is 60N (opposing the direction of motion, which is eastward).
Topper's Solved these Questions
- LAWS OF MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - LAWS OF MOTIONEXERCISE - Check point 5.1
20 Videos
- LAWS OF MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - LAWS OF MOTIONEXERCISE - Check point 5.2
15 Videos
- LAWS OF MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - LAWS OF MOTIONEXERCISE - Comprehension
9 Videos
- KINEMATICS 1BOOK - DC PANDEY ENGLISHCHAPTER - KINEMATICS 1EXERCISE - INTEGER_TYPE
15 Videos
- LAWS OF THERMODYNAMICSBOOK - DC PANDEY ENGLISHCHAPTER - LAWS OF THERMODYNAMICSEXERCISE - Level 2 Subjective
18 Videos
Similar Questions
A crate of mass 20 kg is sliding across a wooden floor. The coefficient of kinetic friction between the crate and the floor is 0.3.
Determine the magnitude of the friction force acting on the crate.
View SolutionA block of mass'm' is resting on the floor of a lift. The coefficient of friction between the block and the floor is μ. When the lift is falling freely, the limiting frictional force between block and surface is
View Solution
Knowledge Check
A crate of mass 100 kg is at rest on a horizontal floor. The coefficient of static friction between the crate and the floor is 0.4, and the coefficient of kinetic friction is 0.3 . A force F of magnitude 344 N is then applied to the crate, parallel to the floor. Which of the following is true ?
AThe crate will accelerate across the floor at 0.5m/s2.BThe static friction force, which is the reaction force to F as guaranteed by Newton 's Third Law, will also have a magnitude of 344 N.CThe crate will slide across the floor at a constant speed of 0.5m/s.DThe crate will not move.A block of mass 1 kg lies on a horizontal surface in a truck. The coefficient of static friction between the block and the surface is 0.6. If the acceleration of the truck is 5m/s2, the frictional force acting on the block is…………newtons.
A10NB5NC2.5ND20N
A body is in contact with the vertical front part of the truck. The coefficient of friction between the body and the truck is μ. The minimum acceleration with which the truck should travel so that the body does not fall down is
View SolutionA block of mass 1 kg lies on a horizontal surface in a truck. The coefficient of static friction between the block and the surface is 0.6. If the acceleration of the truck is 5m/s2, the frictional force acting on the block is…………newtons.
View SolutionA block of mass 4kg pressed againest a rought wall by two perpendicular horizontal forces F1andF2as shown in figure Coefficient of static friction between the block and wall is 0.6 and that of kinetic friction is 0.5
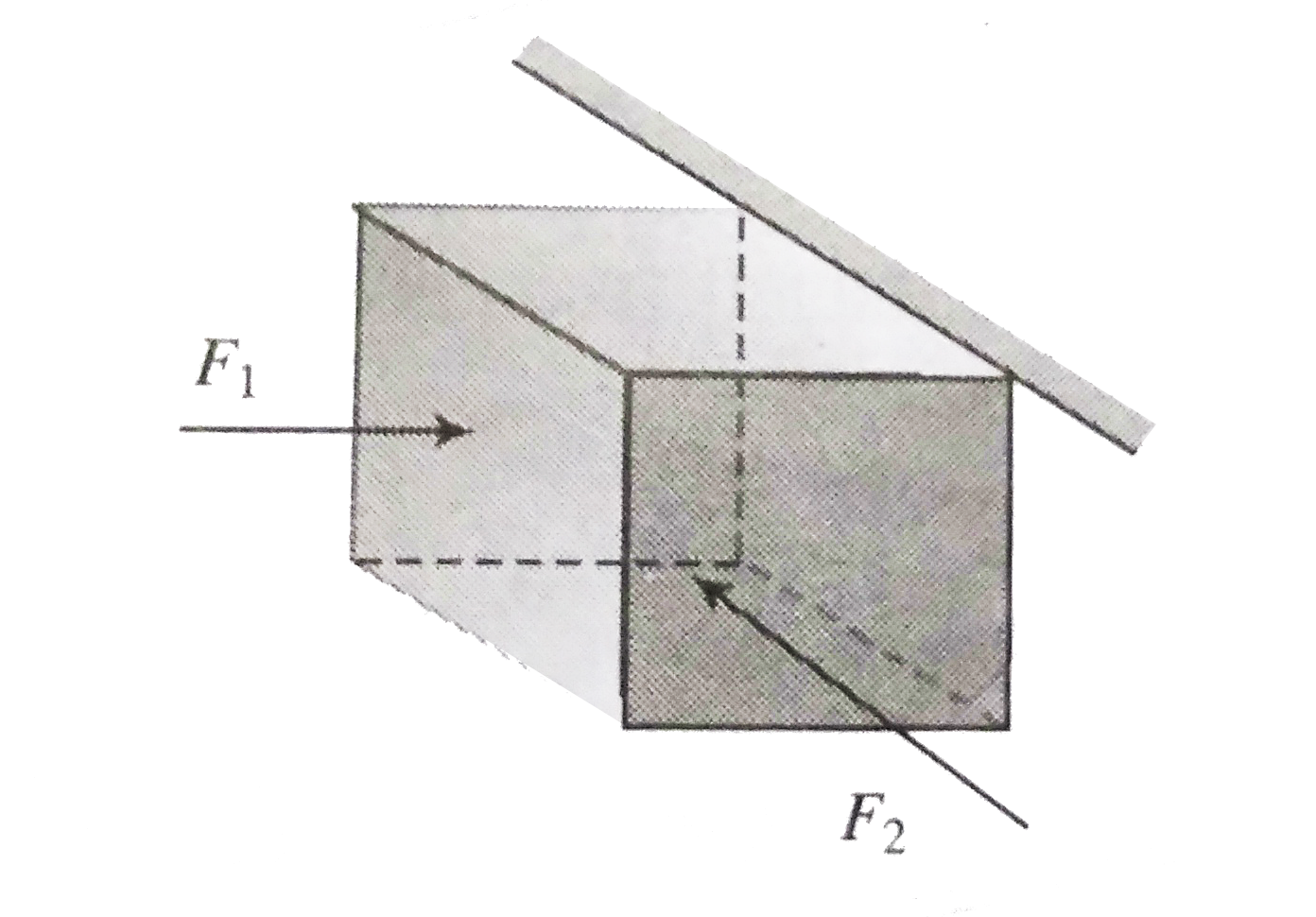
For the data of Q 28 ,Find the magnitude of acceleration of the block
View SolutionA block of mass 1 kg is placed on a truck which accelerates with acceleration 5ms−2. The coefficient of static friction between the block and truck is 0.6. The frictional force acting on the block is
View SolutionA man of mass 75kg is pushing a heavy box on a flat floor. The coefficient of kinetic and static friction between the floor and the box is 0.20, and the coefficient of static friction between the man's shoes and the floor is 0.80. If the man pushes horizontally, what is the maximum values (in kg) of the box he can move?

View SolutionA crate of mass 20 kg is sliding across a wooden floor. The coefficient of kinetic friction between the crate and the floor is 0.3.
If the crate is being pulled by a force of 90 N (parallel to the floor), find the acceleration of the crate.
View Solution
