A particle is moving in a circle of radius 4cm with constant speed of 1cm/s. Find
(a) time period of the particle.
(b) average speed, average velocity and average acceleration in a time interval from t=0 to t=T4. Here, T is the time period of the particle. Give only their magnitudes.
The correct Answer is:A, B, C
To solve the problem step by step, we will break it down into parts (a) and (b).
Part (a): Finding the Time Period of the Particle
1. Identify the Formula for Time Period:
The time period T of a particle moving in a circle is given by the formula:
T=Total DistanceSpeed
The total distance for one complete revolution (circumference of the circle) is 2πr.
2. Substituting the Values:
Given:
- Radius r=4cm
- Speed v=1cm/s
Now, calculate the circumference:
Circumference=2πr=2×3.14×4cm=25.12cm
3. Calculating Time Period:
Substitute the values into the time period formula:
T=25.12cm1cm/s=25.12s
Thus, the time period T is approximately 25.12s.
Part (b): Finding Average Speed, Average Velocity, and Average Acceleration from t=0 to t=T4
1. Average Speed:
Since the particle is moving with constant speed, the average speed is equal to the instantaneous speed:
Average Speed=v=1cm/s
2. Average Velocity:
- Displacement Calculation:
At t=T4, the particle moves 90∘ around the circle. The displacement can be calculated using the Pythagorean theorem. The displacement from point A (starting point) to point B (point after 90∘) is:
Displacement=r√2=4√2cm
- Time Interval:
The time interval from t=0 to t=T4 is:
Δt=T4=25.12s4=6.28s
- Calculating Average Velocity:
Average Velocity=DisplacementΔt=4√2cm6.28s≈0.9cm/s
3. Average Acceleration:
- Change in Velocity:
The initial velocity vi=1cm/s and the final velocity vf can be calculated using the average velocity. Since average velocity is less than the initial speed, we can assume that the final velocity is approximately 0.9cm/s.
- Calculating Average Acceleration:
Average Acceleration=ΔvΔt=vf−viΔt=0.9cm/s−1cm/s6.28s≈−0.016cm/s2
Summary of Results:
- (a) Time Period T≈25.12s
- (b) Average Speed =1cm/s
- Average Velocity ≈0.9cm/s
- Average Acceleration ≈−0.016cm/s2
The time period T of a particle moving in a circle is given by the formula:
T=Total DistanceSpeed
The total distance for one complete revolution (circumference of the circle) is 2πr.
Given:
- Radius r=4cm
- Speed v=1cm/s
Circumference=2πr=2×3.14×4cm=25.12cm
Substitute the values into the time period formula:
T=25.12cm1cm/s=25.12s
Since the particle is moving with constant speed, the average speed is equal to the instantaneous speed:
Average Speed=v=1cm/s
- Displacement Calculation:
At t=T4, the particle moves 90∘ around the circle. The displacement can be calculated using the Pythagorean theorem. The displacement from point A (starting point) to point B (point after 90∘) is:
Displacement=r√2=4√2cm
- Time Interval:
The time interval from t=0 to t=T4 is:
Δt=T4=25.12s4=6.28s
- Calculating Average Velocity:
Average Velocity=DisplacementΔt=4√2cm6.28s≈0.9cm/s
- Change in Velocity:
The initial velocity vi=1cm/s and the final velocity vf can be calculated using the average velocity. Since average velocity is less than the initial speed, we can assume that the final velocity is approximately 0.9cm/s.
- Calculating Average Acceleration:
Average Acceleration=ΔvΔt=vf−viΔt=0.9cm/s−1cm/s6.28s≈−0.016cm/s2
- (a) Time Period T≈25.12s
- (b) Average Speed =1cm/s
- Average Velocity ≈0.9cm/s
- Average Acceleration ≈−0.016cm/s2
Topper's Solved these Questions
- KINEMATICSBook:DC PANDEY ENGLISHChapter:KINEMATICSExercise:Exercise 6.4
Explore 2 Videos
- KINEMATICSBook:DC PANDEY ENGLISHChapter:KINEMATICSExercise:Exercise 6.5
Explore 10 Videos
- KINEMATICSBook:DC PANDEY ENGLISHChapter:KINEMATICSExercise:Exercise 6.2
Explore 3 Videos
- GRAVITATIONBook:DC PANDEY ENGLISHChapter:GRAVITATIONExercise:(C) Chapter Exercises
Explore 45 Videos
- KINEMATICS 1Book:DC PANDEY ENGLISHChapter:KINEMATICS 1Exercise:INTEGER_TYPE
Explore 15 Videos
Similar Questions
A particle is moving in a circle of radius R with constant speed. The time period of the particle is T. In a time t=T6
Average speed of the particle is ……
View SolutionA particle moves in a circle of radius 5 cm with constant speed and time period 0.2πs. The acceleration of the particle is
View SolutionA particle is moving in a circle of radius R with constant speed. The time period of the particle is T. In a time t=T6
Average velocity of the particle is…..
View SolutionA particle moves in a circle of radius R=2122m with constant speed 1m/s. Find,
(a) magnitude of average velocity and
(b) magnitude of average acceleration in 2 s.
View SolutionA particle is moving in a circle of radius R with constant speed. The time period of the particle is t=1. In a time t=T/6, if the difference between average speed and average velocity of the particle is 2ms−1. Find the radius R of the circle (in meters).
View SolutionA particle is moving along a circle of radius R with a uniform speed v. At t=0 , the particle is moving along the east. Find the average acceleration (magnitude and direction) in 1/4th revolution.
View SolutionA particle moves along a circle of radius R with a constant angular speed ω . Its displacement (only magnitude) in time t will be
View SolutionA particle is moving eastwards with a speed of 6 m/s. After 6 s, the particle is found to be moving with same speed in a direction 60∘ north of east. The magnitude of average acceleration in this interval of time is
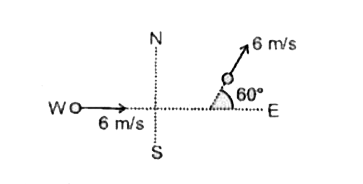
View SolutionA particle with the constant speed in a circle of radius r and time period T.The centripetal acceleration of a particle is
View Solutionvelocity-time graph of a particle moving in a straight line is as shown in figure. At time t=0, velocity of the particle is zero. Find

(a) average acceleration in a time interval from t=6s to t=12s,
(b) velocity of the particle at t=14s.
View Solution

