Two resistances are connected in the two gaps of a meter bridge. The balance point is 20cm from the zero end. When a resistance 15Ω is connected in series with the smaller of two resistance, the null point+ shifts to 40cm. The smaller of the two resistance has the value.
8Ω
9Ω
10Ω
12Ω
The correct Answer is:B
To solve the problem step by step, we will use the principles of a meter bridge and the concept of resistances in series and parallel.
Step 1: Understanding the Meter Bridge
A meter bridge is based on the principle of the Wheatstone bridge. When two resistances are connected in the two gaps of the meter bridge, the balance point (null point) is determined by the ratio of the resistances.
Step 2: Initial Setup
Let:
- R1 = smaller resistance
- R2 = larger resistance
From the problem, we know that the balance point is at 20 cm from the zero end. This means:
R1R2=20100−20=2080=14
Thus, we can express this as:
R1=14R2(Equation 1)
Step 3: Adding Series Resistance
Next, when a resistance of 15 Ω is connected in series with R1, the new balance point shifts to 40 cm. Now, we can write the equation for the new balance point:
R1+15R2=40100−40=4060=23
This can be rearranged to:
R1+15=23R2(Equation 2)
Step 4: Solving the Equations
Now we have two equations:
1. R1=14R2
2. R1+15=23R2
Substituting Equation 1 into Equation 2:
14R2+15=23R2
Step 5: Clear the Fractions
To eliminate the fractions, we can multiply the entire equation by 12 (the least common multiple of 4 and 3):
12(14R2)+12⋅15=12(23R2)
This simplifies to:
3R2+180=8R2
Step 6: Rearranging the Equation
Now, rearranging gives:
180=8R2−3R2
180=5R2
R2=1805=36Ω
Step 7: Finding R1
Now, substituting R2 back into Equation 1 to find R1:
R1=14R2=14×36=9Ω
Conclusion
The smaller of the two resistances R1 is 9Ω.
---
A meter bridge is based on the principle of the Wheatstone bridge. When two resistances are connected in the two gaps of the meter bridge, the balance point (null point) is determined by the ratio of the resistances.
Let:
- R1 = smaller resistance
- R2 = larger resistance
R1R2=20100−20=2080=14
Thus, we can express this as:
R1=14R2(Equation 1)
Next, when a resistance of 15 Ω is connected in series with R1, the new balance point shifts to 40 cm. Now, we can write the equation for the new balance point:
R1+15R2=40100−40=4060=23
This can be rearranged to:
R1+15=23R2(Equation 2)
Now we have two equations:
1. R1=14R2
2. R1+15=23R2
14R2+15=23R2
To eliminate the fractions, we can multiply the entire equation by 12 (the least common multiple of 4 and 3):
12(14R2)+12⋅15=12(23R2)
This simplifies to:
3R2+180=8R2
Now, rearranging gives:
180=8R2−3R2
180=5R2
R2=1805=36Ω
Now, substituting R2 back into Equation 1 to find R1:
R1=14R2=14×36=9Ω
The smaller of the two resistances R1 is 9Ω.
Topper's Solved these Questions
- BOOK - DC PANDEY ENGLISHCHAPTER - EXPERIMENTSEXERCISE - Subjective15videos
EXPERIMENTS
- BOOK - DC PANDEY ENGLISHCHAPTER - EXPERIMENTSEXERCISE - Exercise 3.83videos
EXPERIMENTS
- BOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Integer17videos
ELECTROSTATICS
- BOOK - DC PANDEY ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - Medical entranes gallery49videos
FLUID MECHANICS
Similar Questions
Two resistances are connected in two gaps of a meter bridge. The balance point is 20cm from the zero end. A resistance of 15Ω is connected in series with the smaller of the two. The null point shifts to 40cm. The value of the smaller resistance in Ω is
View SolutionTwo unknown resistances are connected in two gaps of a meter-bridge. The null point is obtained at 40 cm from left end. A 30Ω resistance is connected in series with the smaller of the two resistances, the null point shifts by 20 cm to the right end. The value of smaller resistance in Ω is
View SolutionWith two resistance R1andR2(>R1) in the two gaps of a metre bridge the balance was found to be 1/3 m from the zero end. When a 6Ωresistance is connected in series with the smaller of the two resistance, the point is shifted to 2/3 m from the same end, then R1andR2 are
View SolutionThe figure shows experimental set up of a meter bridge. When the two unknown resistances X and Y are inserted, the null point D is obtained 40 cm from the end A. When a resistance of 10Ω is connected in series with X, the null point shifts by 10 cm. Find the position of the null point when the 10Ω resistance is instead connected in series with resistance 'Y'. Determine the value of the resistance X and Y
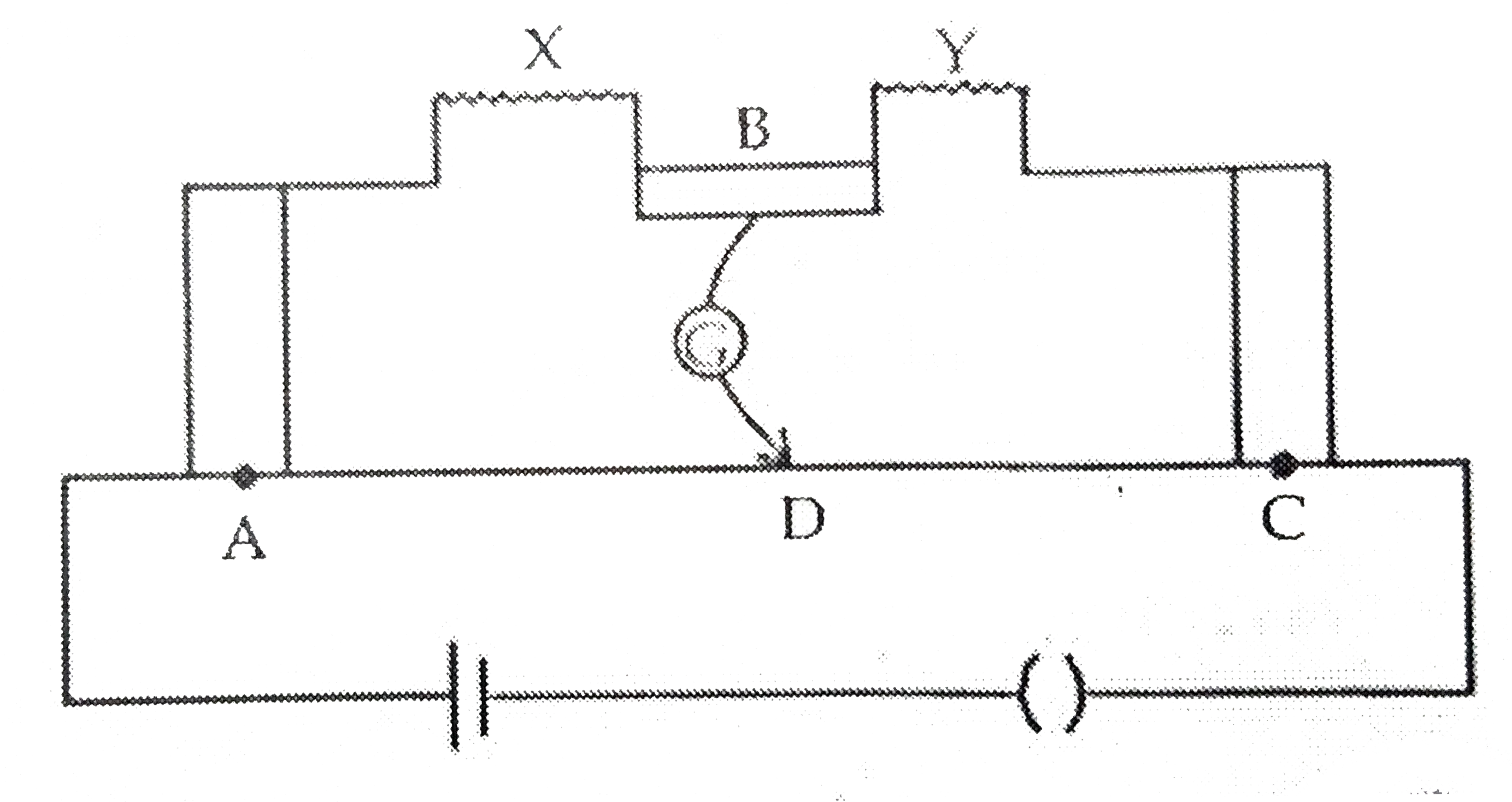 View Solution
View SolutionTwo unkonwn resistances X and Y are connected to left and right gaps of a meter bridge and the balancing point is obtained at 80cm from left. When a 10Ω resistance is connected parallel to X, the balancing point is 50cm from left. The values of X and Y respectively are
View SolutionThe figure
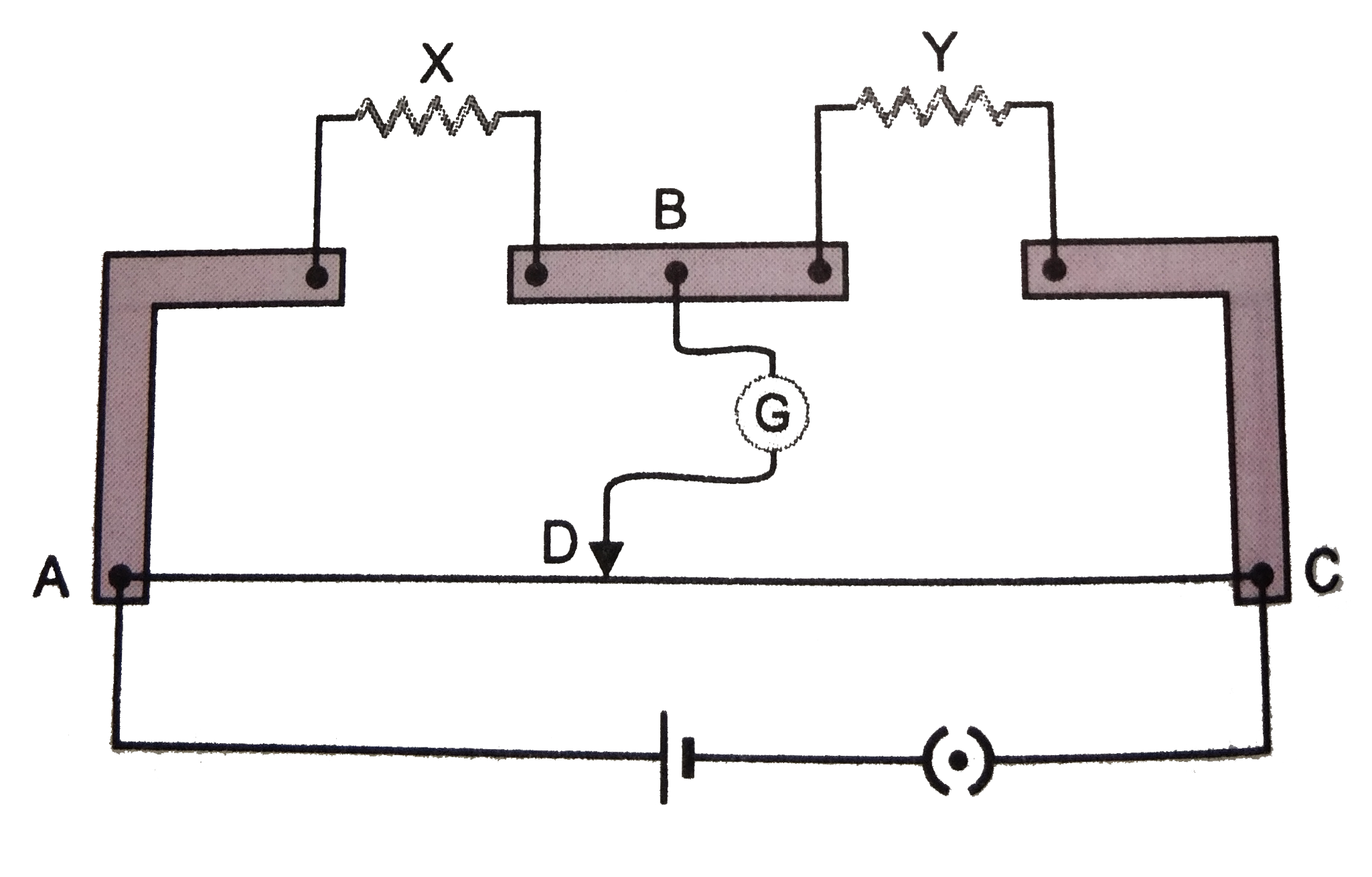
Shows the experimental set up of a meter bridge. The null point is found to be 60 cm away from the end A with X and Y in positions as shown. When a resistance of 15Ω is connected in series with Y, the null points is found to shift by 10 cm towards the end A of the wire. Find the position of the null point if resistance of 30Ω were connected in parallel with Y.View SolutionThe resistance in the left and right gaps of a balanced meter bridge are R1 and R1. The balanced point is 50cm. If a resistance of 24Ω is connected in parallel to R2, the balance point is 70cm. The value of R1 or R2 is.
View SolutionIn a meter bridge, the null point is found at a distance of 40 cm from A. If now a resistance of 12 Ω is connected in parallel with S, the null point occurs at 60 cm from A. Determine the value of R.
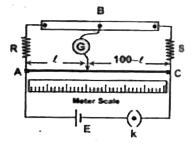 View Solution
View SolutionIn a meter bridge,
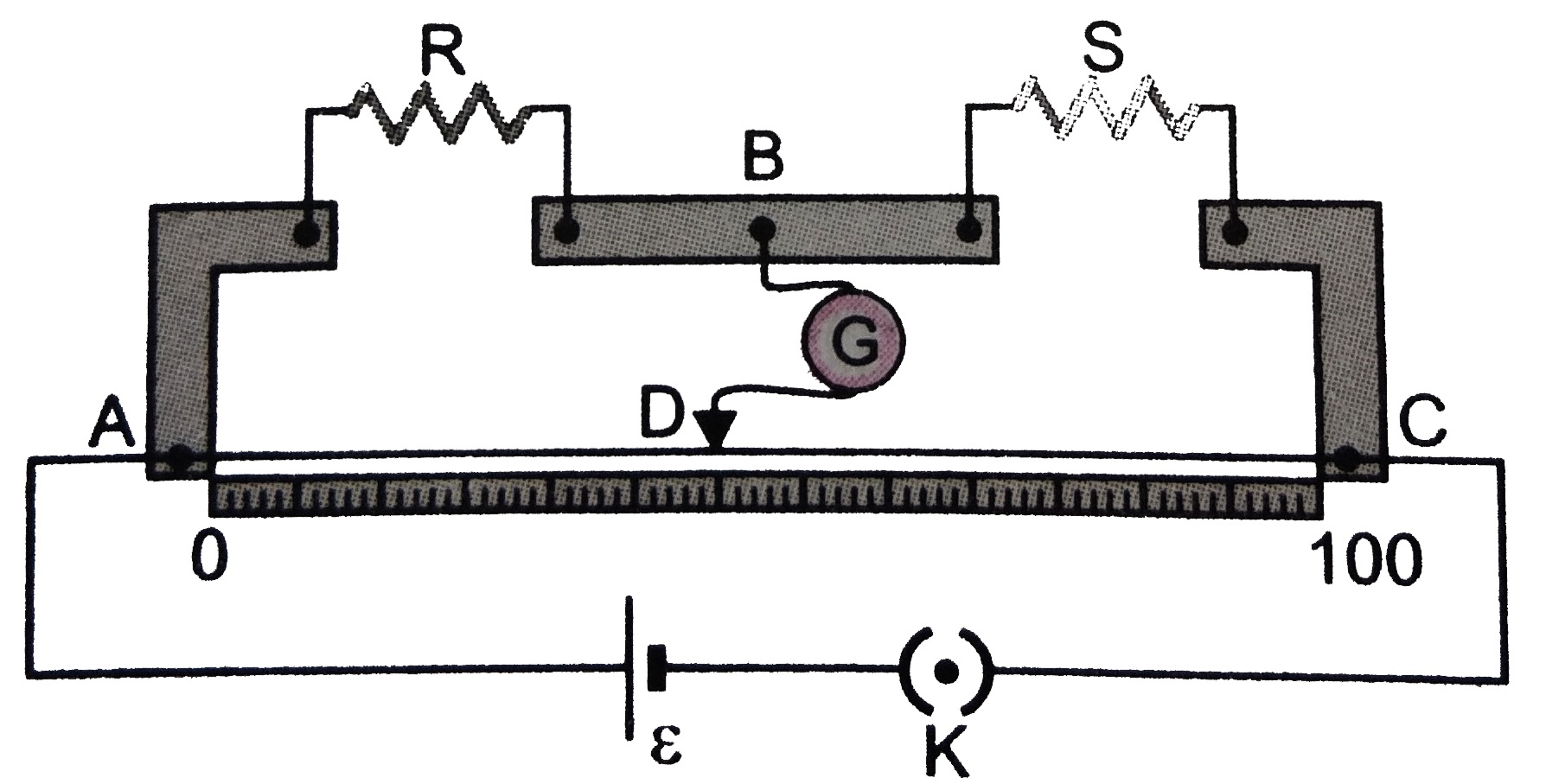
the null points is found at a distance of 33.7 cm from A. If now a resistance of 12Ω is connected in parallel with S, the null point occurs at 51.9 cm. Determine the values of R and S.View SolutionWhen a resistance of 100Ω is connected in series with a galvanometer of resistance R, then its range is V. To double its range, a resistance of 1000Ω is connected in series. Find the value of R.
View Solution
