Radius of a wire is 2.50 mm. The length of the wire is 50.0 cm. If mass of wire was measured as 25g, then find the density of wire in correct significant figures.
[Given,π=3.14,exact]
The correct Answer is:B, C
To find the density of the wire, we will follow these steps:
Step 1: Convert the Measurements
1. Convert the radius from mm to meters:
r=2.50mm=2.50×10−3m
2. Convert the length from cm to meters:
L=50.0cm=50.0×10−2m=0.50m
3. Convert the mass from grams to kilograms:
m=25g=25×10−3kg=0.025kg
Step 2: Calculate the Volume of the Wire
The volume V of the wire can be calculated using the formula for the volume of a cylinder:
V=πr2L
Substituting the values:
V=3.14×(2.50×10−3)2×0.50
Calculating r2:
(2.50×10−3)2=6.25×10−6m2
Now substituting this back into the volume formula:
V=3.14×6.25×10−6×0.50
Calculating:
V=3.14×3.125×10−6=9.8125×10−6m3
Step 3: Calculate the Density of the Wire
Now, we can find the density ρ using the formula:
ρ=mV
Substituting the values:
ρ=0.025kg9.8125×10−6m3
Calculating:
ρ=2547.770701kg/m3
Step 4: Round to Correct Significant Figures
The values given in the problem have the following significant figures:
- Radius: 2.50 mm (3 significant figures)
- Length: 50.0 cm (3 significant figures)
- Mass: 25 g (2 significant figures)
The least number of significant figures is 2 (from mass). Therefore, we round the density to 2 significant figures:
ρ≈2500kg/m3
Final Answer
The density of the wire is ρ=2500kg/m3.
---
1. Convert the radius from mm to meters:
r=2.50mm=2.50×10−3m
L=50.0cm=50.0×10−2m=0.50m
m=25g=25×10−3kg=0.025kg
The volume V of the wire can be calculated using the formula for the volume of a cylinder:
V=πr2L
Substituting the values:
V=3.14×(2.50×10−3)2×0.50
Calculating r2:
(2.50×10−3)2=6.25×10−6m2
Now substituting this back into the volume formula:
V=3.14×6.25×10−6×0.50
Calculating:
V=3.14×3.125×10−6=9.8125×10−6m3
Now, we can find the density ρ using the formula:
ρ=mV
Substituting the values:
ρ=0.025kg9.8125×10−6m3
Calculating:
ρ=2547.770701kg/m3
The values given in the problem have the following significant figures:
- Radius: 2.50 mm (3 significant figures)
- Length: 50.0 cm (3 significant figures)
- Mass: 25 g (2 significant figures)
ρ≈2500kg/m3
The density of the wire is ρ=2500kg/m3.
Topper's Solved these Questions
- MEASUREMENT AND ERRORSBOOK - DC PANDEY ENGLISHCHAPTER - MEASUREMENT AND ERRORSEXERCISE - Exercise 2.1
2 Videos
- MEASUREMENT AND ERRORSBOOK - DC PANDEY ENGLISHCHAPTER - MEASUREMENT AND ERRORSEXERCISE - Exercise 2.2
1 Video
- MAGNETIC EFFECT OF CURRENT AND MAGNETISMBOOK - DC PANDEY ENGLISHCHAPTER - MAGNETIC EFFECT OF CURRENT AND MAGNETISMEXERCISE - Integer type Questions
10 Videos
- MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - MOTIONEXERCISE - Medical entrances gallery
19 Videos
Similar Questions
In an experiment, current measured is, I=10.0A, potential difference measured is V=100.0V, length of the wire is 31.4cm and the diameter of the wire 2.00mm (all in correct significant figures). Find resistivity of the wire in correct significant figures. [Take π=3.14, exact].
(a)
(b)
(c)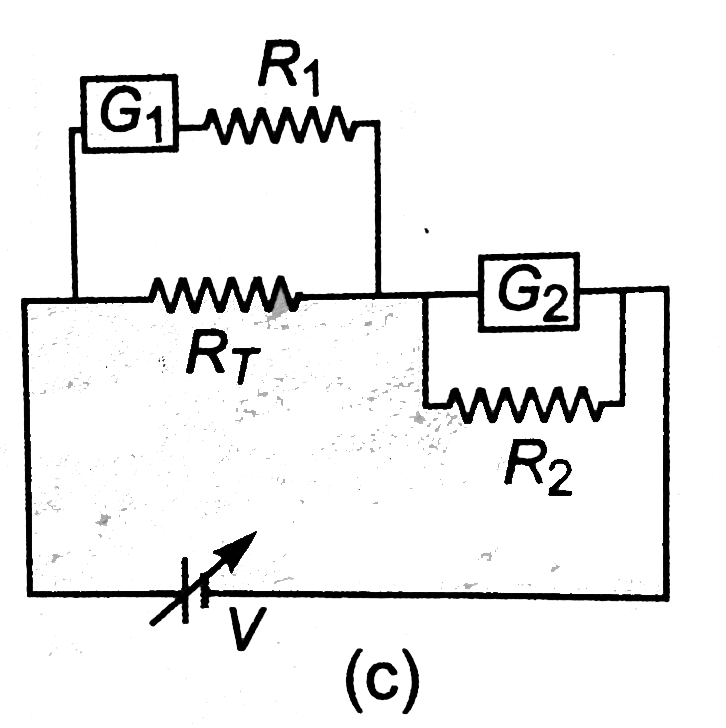
(d)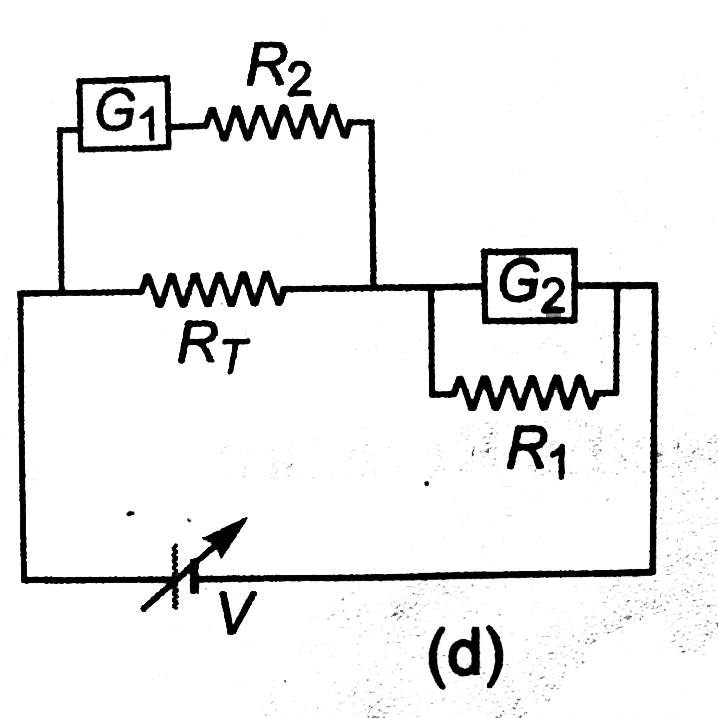 .
.
View SolutionFrom some instruments current measured is I=10.0amp, potential different measured is V=100.0V, length of wire is 31.4cm, and diameter of wire is 2.00mm (all in correct significant figure). The resistivity of wire (in correct significant figures)will be (use π=3.14)
View SolutionA thin wire has a length of 21.7 cm and radius 0.46 mm. Calculate the volume of the wire to correct significant figures.
View SolutionIf the length of the cylinder is measured as 25mm and mass of the cylinder is measured as 50.0gm find the density of the cylinder (gm/cm3) in proper significant .
View SolutionA thin wire has length of 21.7 cm and radius 0.46 mm. Calculate the volume of the wire to correct significant figures?
View SolutionA thin wire has length of 21.7 cm and radius 0.46 mm. Calculate the volume of the wire to correct significant figures?
View SolutionIf the length of wire is (100.0 cm) and radius of wire as measured from screw gauge is (1.00mm) then the specific resistance of wire material is .
View SolutionThe pitch of a screw gauge is 1mm and there are 100 divisions on circular scale. While measuring the diameter of a wire, the linear scale reads 1 mm and 47th division on circular scale coincides with reference line. The length of the wire is 5.6 cm. Find the curved surface area of the wire in cm2 to correct number of significant figures.
View SolutionThe diameter of a sphere is 6 cm. It is melted and drawn into a wire of diameter 0-2 cm. Find the length of the wire.
View SolutionThe diameter of a sphere is 6cm. It is melted and drawn into a wire of diameter 0.2 cm. Find the length of the wire.
View Solution
