एक त्रिभुज के शीर्ष तथा मूल बिन्दु है। यदि त्रिभुज का क्षेत्रफल हो, तो का मान है -
The correct Answer is:A
Step by step video, text & image solution for एक त्रिभुज के शीर्ष ("cos"alpha, "sin"alpha), ("sin"alpha, "cosalpha) तथा मूल बिन्दु है। यदि त्रिभुज का क्षेत्रफल "sin"^(2)alpha हो, तो alpha का मान है - by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
व्यंजकों x6−y6,xy3+x3y−x2y2,x4+y3x का महत्तम समापवर्तक होगा|
View Solutionदी गई आकृति में x का मान ज्ञात कीजिए।
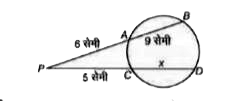
View SolutionIf A=[[cosalpha, -sin alpha] , [sin alpha, cos alpha]] then A+A'=I then alpha=
View SolutionIf A=[[cosalpha, sin alpha] , [-sin alpha, cos alpha]] and A^(-1)=A' then alpha=
View Solutionयदि A=[cosαsinαsinαcosα] तो ज्ञात कीजिए 2A' और AA'
View Solutionमान A(2,−3) तथा B(−2,1) एक त्रिभुज ABC के शीर्ष है। यदि इस त्रिभुज का केन्द्रक सरल रेखा 2x+3y=1 पर भ्रमण करता है, तो शीर्ष C का बिन्दुपथ है:
View Solutionमाना α तथा β समीकरण px2+qx+r=0,p≠0 के मूल हैं। यदि p,q, r समान्तर श्रेढ़ी में हैं तथा 1α+1β=4 है, तो |α−β | का मान है
View Solutionयदि समीकरण x2−2x+2=0 के मूल α तथा β हैं, तो n का न्यूनतम मान, जिसके लिए (αβ)n=1 है
View Solutionयदि द्विघाती समीकरण, x2+xsinθ−2sinθ=0,θ∈(0,π2), के मूल α तथा β हैं , तो α12+β12(α−12+β−12).(α−β)24 बराबर है
View Solutionएक त्रिभुज का एक शीर्ष (1,2) पर है तथा इससे होकर जाने वाली दो भुजाओं के मध्य - बिन्दु (−1,1) और (2,3) हैं , तो इस त्रिभुज का केन्द्रक है
View Solutionयदि एक त्रिभुज , जिसका एक शीर्ष परवलय के शीर्ष परवलय y2+4(x−a2)=0 तथा अन्य दोनों शीर्ष y-अक्ष तथा परवलय के प्रतिच्छेदन बिंदुओं पर हैं , का क्षेत्रफल 250 वर्ग इकाई है , तो 'a' का एक मान है
View Solutionयदि z−αz+α(α∈R) एक शुद्ध रूप से काल्पनिक संख्या है तथा |z|=2 है तो α का एक मान है
View Solutionजहाँ ∣∣α2−β2∣∣=74 जहाँ α,β समीकरण 2x2+7x+c=0 के मूल हो, तो c का मान है।
View Solutionयदि tanα व् tanβ समीकरण x2−px+q=0 के मूल हो, तो sin2(α+β) का मान है
View Solutionयदि समीकरण px2+qx+r=0 के मूल sinα व cosα हों, तो
View SolutionEliminate α between the equations :
sin2αcosα=a3andcos2αsinα=b3
View Solution
