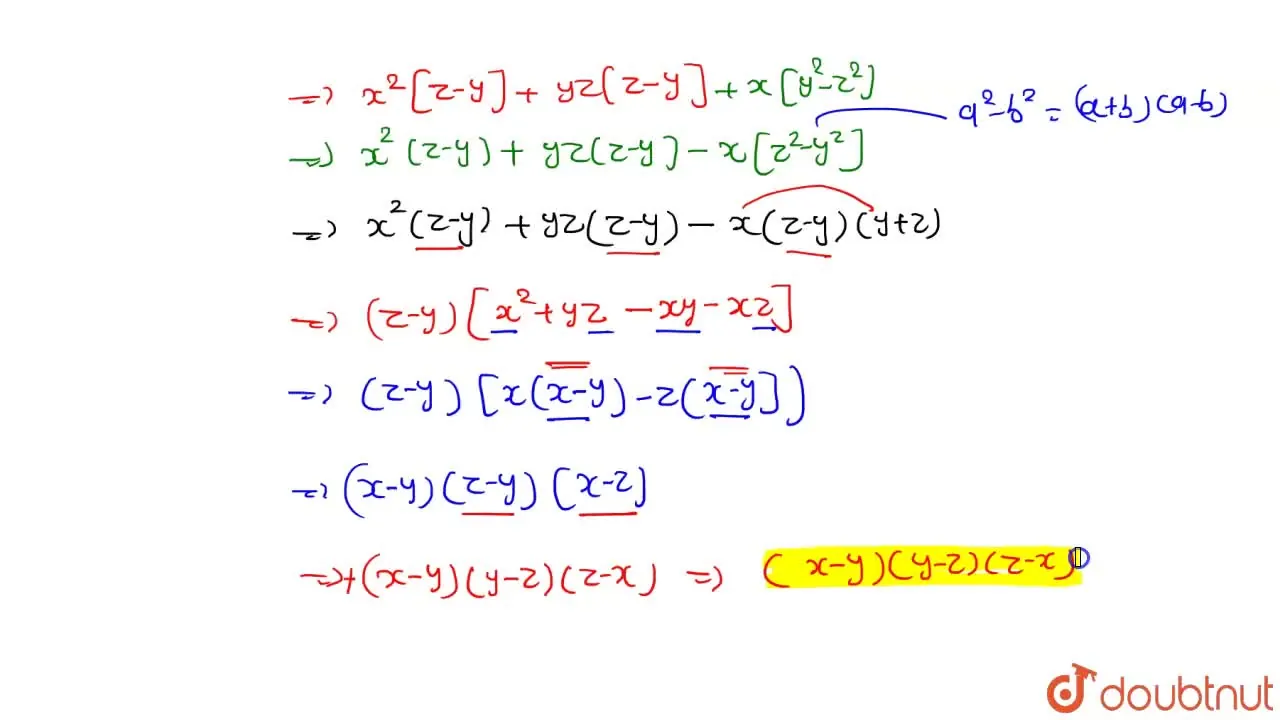गुणनखण्ड कीजिए -
x(y2−z2)+y(z2−x2)+z(x2−y2).
(x+y)(y+z)(z+x)
(x−y)(x−z)(z−y)
(x+y)(z−y)(x−z)
(y−x)(z−y)(x−z)
The correct Answer is:D
Step by step video, text & image solution for गुणनखण्ड कीजिए - x(y^(2)-z^(2))+y(z^(2)-x^(2))+z(x^(2)-y^(2)). by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Related Playlists
- BOOK - ARIHANT PUBLICATION BIHARCHAPTER - बहुपद एवं गुणनखण्ड EXERCISE - अभ्यास प्रश्न24videos
बहुपद एवं गुणनखण्ड
- BOOK - ARIHANT PUBLICATION BIHARCHAPTER - प्रिज्म, पिरामिड तथा शंकु EXERCISE - अभ्यास प्रश्न25videos
प्रिज्म, पिरामिड तथा शंकु
- BOOK - ARIHANT PUBLICATION BIHARCHAPTER - बिहार पॉलिटेक्निक प्रवेश परीक्षा मॉडल सॉल्वड पेपर 2016EXERCISE - बहु-विकल्पिय प्रश्न30videos
बिहार पॉलिटेक्निक प्रवेश परीक्षा मॉडल सॉल्वड पेपर 2016
Similar Questions
(x3+x−3x2−3) का गुणन होगा
06:40View Solutionयदि h, c और v क्रमश: एक शंकु की ऊँचाई, वक्रपृष्ठ और शंकु का आयतन हैं, तो 3πvh3−c2h2+9v2 का मान है
01:39View Solutionसमीकरण y2/3−2y1/3=15 का हल है
08:07View SolutionProve the identities: ∣∣ ∣ ∣∣zxyz2x2y2z4x4y4∣∣ ∣ ∣∣=∣∣ ∣ ∣∣xyzx2y2z2x4y4z4∣∣ ∣ ∣∣=∣∣ ∣ ∣∣x2y2z2x4y4z4xyz∣∣ ∣ ∣∣ =x y z (x-y)(y-z)(z-x)(x+y+z)
01:32View Solutiony2+yz+z2(x−y)(x−z)+z2+zx+x2(y−z)(y−x)+x2+xy+y2(z−x)(z−y)
08:39View SolutionProve that : ∣∣ ∣ ∣∣(y+z)2x2x2y2(x+z)2y2z2z2(x+y)2∣∣ ∣ ∣∣=2xyz(x+y+z)3
01:52View SolutionThe following steps are involved in finding the value of (ax+y)x−y(ay+z)y−z(az+x)z−x. Arrange them in sequantial order.
(A) a(x+y)(x−y).ay+z(y−z).a(z+x)(z−x)
(B)a0=1
(C) ax2−y2.ay2−z2.az2−x2
(D) ax2−y2+y2−z2+z2−x203:28View SolutionProve that ∣∣ ∣ ∣∣x2x2−(y−z)2yzy2y2−(z−x)2zxz2z2−(x−y)2xy∣∣ ∣ ∣∣
=(x−y)(y−z)(z−x)(x+y+z)(x2+y2+z2)03:24View Solutionगुणनखण्ड कीजिए : (x−y+z)2+(y−z+x)2+2(x−y+z)(y+z+x).
03:24View SolutionThe value of x2(x−y)(x−z)+y2(y−z)(y−x)+z2(z−x)(z−y) is :
03:24View Solutionx2(y−z)+y2(z−x)+z2(x−y) के गुणनखण्ड ज्ञात कीजिए।
09:08View Solutionगुणनखंड कीजिए :
x2(y−z)+y2(z−x)+z2(x−y)08:43View Solutionगुणनखंड कीजिए :
x2(y−z)+y2(z−x)+z2(x−y)03:41View SolutionProve that : ∣∣ ∣ ∣∣(y+z)2x2x2y2(x+z)2y2z2z2(x+y)2∣∣ ∣ ∣∣=2xyz(x+y+z)3
08:36View SolutionProve the identities: ∣∣ ∣ ∣∣zxyz2x2y2z4x4y4∣∣ ∣ ∣∣=∣∣ ∣ ∣∣xyzx2y2z2x4y4z4∣∣ ∣ ∣∣=∣∣ ∣ ∣∣x2y2z2x4y4z4xyz∣∣ ∣ ∣∣ =x y z (x-y)(y-z)(z-x)(x+y+z)
02:40View Solution