वर्णक्रम के दृश्य क्षेत्र में ध्रुवण तल का घूर्णन θ=a+bλ2 द्वारा दिया जाता है। किसी निश्चित पदार्थ के लिये λ=5000A पर प्रकाशीय घूर्णन 30° प्रति मिमी एवं λ=4000A पर प्रकाशीय घूर्णन 50° प्रति मिमी प्राप्त होता है। नियतांक a का मान होगा|
+50∘9 per mm
−50∘9 per mm
+9∘50 per mm
−9∘50 per mm
The correct Answer is:B
θ=a+bλ2
30=a+b(5000)2 and 50=a+b(4000)2
Solving for a, we get a=−50∘9 per mm
Topper's Solved these Questions
Similar Questions
एक मोल आदर्श गैस समतापीय प्रसार द्वारा गुजरता है। जब इसे Q ऊष्मा दी जाती है। दिया ग्राफ आयतन V तथा Q के मध्य दिखाया गया है। गैस का तापमान लगभग होगा : (R= 8.31 J/K.mole)
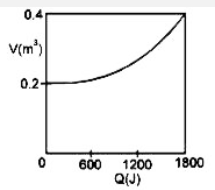
View SolutionCO2 के लिए संपीडीयता गुणांक परिकलित कीजिए, यदि इसका एक मोल 300 K तथा 40 atm पर 0.4 लीटर धेरता है, परिणाम पर वक्तव्य दीजिए।
View Solutionनिम्न कथन सत्य है अथवा असत्य-
उद्देश्य फलन का अधिकतम मान, परिबद्ध क्षेत्र के किसी एक शीर्ष पर होता है।
View Solutionयदि बिंदु (3,4) समीकरण 3y=ax+6 के आलेख पर स्थित है , तो a का मान होगा :
View Solutionघूर्णन द्रव प्रश्न पात्र की दीवारों पर द्रव द्वारा बल
View Solutionसाधारणतया एक कार्बन-कार्बन दीव-बंध के अनुदिश घूर्णन करने के लिए अवरोध काफी अधिक होता है, लेकिन योगिक P में , दो वलयो के मध्य NMR द्वारा दिव-बंध देखा गया जिसका घूर्णन ऊर्जा अवरोध केवल 20 Cal /mol है, इससे पता चलता है की इसमें बहुत से एकल बंध लक्षण होते है ।
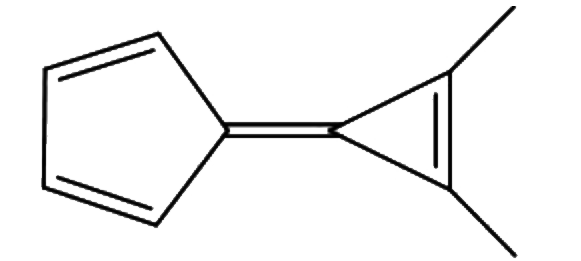
इसका कारण है कि:
View Solutionग्रेफाइट इलेक्ट्रॉड का उपयोग करके जलीय CuSO_4 विलयन के विद्युत्अपघटन पर विलयन में कौन सा पदार्थ प्राप्त होता है?
View Solutionएक शुद्ध प्रतिबिंब रूपी समावयवी का विशिष्ट घूर्णन +10^(@) है। यदि इसे 30% रेसिमीकरण और 70% प्रतिलोमन के साथ एक अभिक्रिया से पृथक किया जाता है, तो प्रेक्षित घूर्णन है:
View Solutionक्लोरीन गैस को MnO_2 और NaCl के साथ H_2SO_4 की अभिक्रिया द्वारा निर्मित किया जाता है। यदि अभिक्रिया में 50 g NaCl का उपयोग किया जाता है, तो STP पर Cl_2 के कितने आयतन का निर्माण होगा?
View Solutionएक पाइरैनोस (pyranose) के alpha -रूप का प्रकाशिक घूर्णन +150.7° है, जबकि beta - रूप का प्रकाशिक घूर्णन +52.8° होता है। विलयन में, इन ऐनोमरों के साम्य मिश्रण का प्रकाशिक घूर्णन +80.2° होता है। साम्य मिश्रण में alpha -रूप की प्रतिशतता कितनी है?
View Solutionध्रुवण का अर्थ होता है, "एक निकटतम स्थित धनायन द्वारा ऋणायन की आकृति में विकृति"। ध्रुवण के बारे में निम्नलिखित में से कौन सा कथन सही है?
View Solutionग्लूकोज के ताजा तैयार विलयन से समय के साथ प्रकाशिक घूर्णन में परिवर्तन को निम्न में जाना जाता है -
View Solutionशर्करा के ताजे तैयार किए गए विलयन में समय के साथ प्रकाशिक घूर्णन में होने वाले परिवर्तन को किस रुप में जाना जाता है?
View Solution400 K ताप पर, 20 लीटर के एक पात्र में 0.4 atm दाब पर CO2(g) और SrO का आधिक्य (ठोस SrO के आयतन की उपेक्षा कीजिए) उपस्थित होता है | अब पात्र में लगे गतिशील पिस्टन को गतिमान करके पात्र का आयतन कम कर दिया जाता है | जब CO2 का दाब अपना अधिकतम मान प्राप्त करता है तो पात्र का अधिकतम आयतन क्या होगा ? (दिया गया है कि: SrCO3(S)⇔SrO(s)+CO2(g),Kp=1.6atm)
View Solutionयदि एक विशिष्ट विलायक में, एक यौगिक द्वारा समतल ध्रुवित प्रकाश का कोई घूर्णन नहीं होता है, यद्यपि यह किरैल है, तो इसका अर्थ हो सकता है कि
View Solutionएथिल ऐल्कोहॉल का K_2Cr_2O_7 के साथ ऑक्सीकरण कराने पर प्राप्त होता है:
View Solution
