माना की f1:R→R2,f2:[0,∞)→R,f3:R→R और f4:R→[0,∞) निम्नानुसार
f1(x)={|x| यदि x<0ex यदि x≥0
f3x={sinx यदि x<0x यदि x≥0
f4(x)={f2(f1(x)) यदि x<0f2(f1(x))−1 यदि x≥0 परिभाषित है 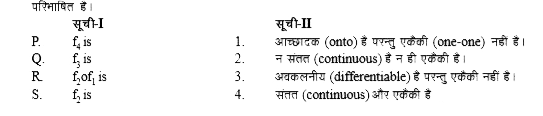
P-3, Q-1, R-4, S-2
P-1, Q-3, R-4, S-2
P-3, Q-1, R-2, S-4
P-1, Q-3, R-2, S-4
The correct Answer is:D
Step by step video, text & image solution for माना की f_(1) : R to R_(2), f_(2) : [0,oo) to R, f_(3) : R to R" और "f_(4) : R to [0,oo)" निम्नानुसार " f_(1) (x)={{:(,|x|, " यदि "x lt 0),(,e^(x)," यदि "x ge 0):} f_(3)x={{:(,sin x," यदि "x lt 0),(,x," यदि "x ge 0):} f_(4)(x)={{:(,f_(2)(f_(1)(x))," यदि "x lt 0),(,f_(2) (f_(1) (x))-1," यदि "x ge 0):} परिभाषित है by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- फलन की सीमा सत्त्यता तथा अवकलनीयता Book:BANSAL HINDIChapter:फलन की सीमा सत्त्यता तथा अवकलनीयता Exercise:Exercise -3 Section -B (LIMITS)
Explore 7 Videos
- फलन की सीमा सत्त्यता तथा अवकलनीयता Book:BANSAL HINDIChapter:फलन की सीमा सत्त्यता तथा अवकलनीयता Exercise:Exercise -3 Continuity And Differentiability
Explore 5 Videos
- फलन की सीमा सत्त्यता तथा अवकलनीयता Book:BANSAL HINDIChapter:फलन की सीमा सत्त्यता तथा अवकलनीयता Exercise:Exercise -2 Section -C [DERIVABILITY]
Explore 12 Videos
- क्रमचय एवं संचय Book:BANSAL HINDIChapter:क्रमचय एवं संचय Exercise:EXERCISE-5 (RANK BOOSTER )
Explore 12 Videos
- वृतBook:BANSAL HINDIChapter:वृतExercise:EXERCISE - 5
Explore 10 Videos
Similar Questions
माना की f:R→R एक धनात्मक वर्धमान फलन है जिसके लिए limx−∞f(3x)f(x)=1. तब limx−∞f(2x)f(x)=
View Solutionमाना f(x)={(x−1)sin1x−1यदिx≠10यदिx=1 तो निम्न में से कौन सा सत्य है
View Solutionयदि फलन f(x)=⎡⎣−x22for x≤0xnsin1xfor x>0,x=0 पर सतत तो है लेकिन अवकलनीय नही हो, तोn का परिसर ज्ञात करो।
View Solution8 चप्पु वाले नाव के सदस्यो को 11 पुरुषों में से चयनित करना है। जिसमें से 5 केवल स्ट्रोक साइड, 4 केवल बो साइड और बाकि दो किसी भी तरफ लिये जा सकते है। कुल कितने चयन संभव है?
View Solutionएक बिन्दु एक ऐसे वृत्त (x+4)2+(y+2)2=25 के अनुदिश गतिमान है जिसका केन्द्र C है। वह वृत्त से बिन्दु A या बिन्दु B पर अलग हो जाता है तथा स्पर्श रेखा के अनुदिश गति करता हुआ बिन्दु D (3.-3) से गुजरता है। निम्न को ज्ञात कीजिये।
(i) A व B पर स्पर्श रेखाओं के समीकरण
(ii) A व B के निर्देशांक
(iii) कोण ADBC व् D की वृत्त से अधिकतम व न्यूनतम दूरी
(iv) चतुर्भुज ADBC व त्रिभुज DAB का क्षेत्रफल
(v) त्रिभुज DAB के परिवृत्त का समीकरण तथा इस वृत्त के द्वारा निर्देशी अक्षों पर काटे गये अन्तः खण्ड
View SolutionFor x varepsilon R,x!=0,x!=1, Let f_(0)(x)=(1)/(1-x) and f_(n+1)(x)=f_(0)(f_(n)(x)),n=0,1,2,3...... Then the value of f_(100)(3)+f_(1)((2)/(3))+f_(2)((3)/(2)) is equal to:
View SolutionLet f(1):R→R,f2:[0,∞)→R,f3:R→Randf4:R→[0,∞) be a defined by
f1(x)={|x|if x<0exif x>0:f2(x)=x2,f3(x)={sinxif x<0xif x≥0 and f4(x)={f2(f1(x))if x<0f2(f1(f1(x)))−1if x≥0 Then, f4 is
View SolutionFor x∈R,x≠0,1, let f0(x)=11−xandfn+1(x)=f0(fn(x)),n=0,1,2….. Then the value of f100(3)+f1(23)+f2(32) is equal to
View SolutionLet f1(x)andf2(x) be twice differentiable functions where F(x)=f1(x)+f2(x)andG(x)=f1(x)−f2(x),∀x∈R,f1(0)=2andf2(0)=1.Iff'1(x)=f2(x)andf'2(x)=f1(x),∀x∈R. then the number of solutions of the equation (F(x))2=9x4G(x)is...... .
View SolutionLet f1:R→R,f2:[0,∞)→R,f3:R→R be three function defined as
f1(x)={|x|x<0exx≥0,f2(x)=x2,f3(x)={f2(f1(x))x<0f2(f1(x))−1x≥0 then f3(x) is:
View Solutionमाना कि फलन
f1:R→R,f2:(−π2,π2)→R,f3:(−1,eπ2−2)→R और f4:R→R इस प्रकार परिभाषित है कि
(i) f1(x)=sin(√1−e−x2),
(ii) f2(x)={|sinx|tan−1xifx≠01ifx=0 जहां प्रतिलोम त्रिकोणमितीय फलन tan−1x,(−π2,π2) में मान धारण करता है
(iii) f3(x)=[sin(loge(x+2))], जहां tεR के लिए [t],t से छोटा या t के बराबर महत्तम पूर्णांक को दर्शाता है।
(iv) f4(x)=⎧⎨⎩x2sin(1x)यदिx≠0xयदिx=0

View SolutionSupposed that f_(1):RtoR,f_(2):[0,oo)toR,f_(3):RtoR And f_(4):rto[0,oo) As follows f_(1)(x)={((|x),यदि,xlt0),(e^(x),यदि,xge0):} f_(2)(x)=x^(2) f_(3)(x)={(sinx, यदि,xlt0),(x, यदि,xge0):} And f_(a)(x)={(f_(2)(f_(1)(x)),यदि,xlt0),(f_(2)(f_(1)(x))-1,यदि ,xge0):}
View SolutionF(x) को दो वास्तविक फलनों f1(x),x∈IR, तथा f2(x)={sin1xयदिx≠00यदिx=0
के गुणनफल के रूप में निम्न प्रकार | 0, यदि x = 0 है से परिभाषित कीजिये F(x)={f1(x)f2(x)यदिx≠00यदिx=0
कथन-1: Fx, IR पर सतत् है।
कथन-2 : f1(x) तथा f2(x) , IR पर सतत् है।
View Solutionयदि fn(x)=efn−1(x)∀n∈N तथा f0(x)=x तो प्रदर्शित कीजिए कि ddx{fn(x)}=f1(x).f2(x)........fn(x) है।
View SolutionFor x∈R,x≠0,x≠1, let f0(x)=11−x and fn+1(x)=f0(fn(x)),n=0,1,2,.... Then the value of f100(3)+f1(23)+f2(32) is equal to
View Solution

