Let f:R→R be defined by f(x)={(x+2,(x≤−1)),(x2,(−1≤x≤1)),(2−x),(x≥1)). Then the value of f(−1.75)+f(0.5)+f(1.5) is Solution in Telugu
The correct Answer is:4
Step by step video, text & image solution for Let f: R rarrR be defined by f(x)={{:(x+2, (xle-1)),(x^(2), (-1lexle1)),(2-x), (xge1)):}. Then the value of f(-1.75)+f(0.5)+f(1.5) is by Maths experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- MAXIMA AND MINIMA BOOK - AAKASH SERIESCHAPTER - MAXIMA AND MINIMA EXERCISE - ADDITIONAL PRACTICE EXERCISE (LEVEL - II (PRACTICE SHEET )(ADVANCED)) (MORE THAN ONE CORRECT ANSWER TYPE QUESTIONS)
11 Videos
- MAXIMA AND MINIMA BOOK - AAKASH SERIESCHAPTER - MAXIMA AND MINIMA EXERCISE - ADDITIONAL PRACTICE EXERCISE (LEVEL - II (PRACTICE SHEET )(ADVANCED)) (MATRIX MATCHING TYPE QUESTIONS)
2 Videos
- MAXIMA AND MINIMA BOOK - AAKASH SERIESCHAPTER - MAXIMA AND MINIMA EXERCISE - ADDITIONAL PRACTICE EXERCISE (LEVEL - II (LECTURE SHEET )(ADVANCED)) (LINKED COMPREHENSION TYPE QUESTIONS)
6 Videos
- MAXIMA & MINIMABOOK - AAKASH SERIESCHAPTER - MAXIMA & MINIMAEXERCISE - EXERCISE-III
35 Videos
- MEAN VALUE THEOREMSBOOK - AAKASH SERIESCHAPTER - MEAN VALUE THEOREMSEXERCISE - PRACTICE SHEET (EXERCISE-I (LEVEL-II (MORE THAN ONE CORRECT ANSWER TYPE QUESTIONS ) )
2 Videos
Similar Questions
For function f(x)=xcos1x,x≥1,(2009)
View SolutionMatch the following Column I to Column II
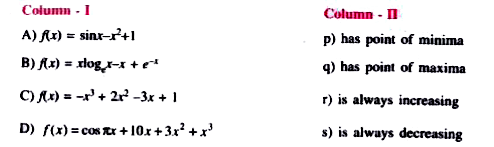
View SolutionSuppose you do not know the function f(x) , however some information about f(x) is listed below. Read the following carefully before attempting the questions
(i) f(x) is continuous and defined for all real numbers
(ii) f'(-5)=0 , f'(2) is not defined and f'(4)=0
(iii) (-5,12) is a point which lies on the graph of f(x)
(iv) f"(2) is undefined , but f"(x) is negative everywhere else.
(v) the signs of f(x) is given below

On the possible graph of y=f(x) we have
View SolutionThe maximum slope of the curve y=−x3+3x2+9x−27 is
View SolutionGiven f(x) = 4- ((1)/(2) - x)^(2//3) , g(x) = {:{((tan[x])/(x),","x cancel(=)0),(1,","x=0):}" "h(x)={x}, k (x) = 5^(log_(2)(x+3))
Then in [0,1], Lagrange's mean value theorem is not applicable to (where [.] and {.} represents the greatest integer functions and fractions part functions, respectively )
View SolutionLet f(x) be a real valued function defined for all x≥1, satistying f(1)=1 and f'(x)=1x2+(f(x)), then limx→∞f(x)
View SolutionIf the function f is defined by
f(x)={(x+2, ifx>1),(2 if-1lexle1),(x−1 if−3<x<−1):} find the values of
f(3)
View SolutionIf the function f is defined by
f(x)={(x+2, ifx>1),(2 if-1lexle1),(x−1 if−3<x<−1):} find the values of
f(0)
View SolutionIf the function f is defined by
f(x)={(x+2, ifx>1),(2 if-1lexle1),(x−1 if−3<x<−1):} find the values of
f(-1.5)
View SolutionIf the function f is defined by
f(x)={(x+2, ifx>1),(2 if-1lexle1),(x−1 if−3<x<−1):} find the values of
f(2)+f(-2)
View SolutionLet f:R→R be defined by f(x)={(x+2,(x≤−1)),(x2,(−1≤x≤1)),(2−x),(x≥1)). Then the value of f(−1.75)+f(0.5)+f(1.5) is
View SolutionLet f:[2,∞)→R be the function defined by f(x)=x2−4x+5, then the range of f is
View SolutionIf f is defined by f(x)={x for 0≤x<12−x for x≤1 then at x =1
View SolutionLet f:R→R be defined by
f(x)=⎧⎪⎨⎪⎩2xx>3x21<x≤33xx≤1
Then f(-1) + f(2) + f(4) is
View SolutionLet f:R−{1}→R be defined by
f(x)=1+x1−x∀x∈R−{1} then for x≠±1,1+f(x)2f(x)f(x2)=………….
View SolutionIf f:R→R is defined by f(x)=x2−3x+2 , find f(f(x)).
View Solution
