Let f(x)) be an increasing function defined on (0.∞) If f(2a2+a+1)>f(3a2−4a+1), then the possible integers in the range of a is /areSolution in Telugu
1
2
3
4
The correct Answer is:B, C, D
Step by step video, text & image solution for Let f(x)) be an increasing function defined on (0.oo) If f(2a^(2)+a+1)gtf(3a^(2)-4a+1), then the possible integers in the range of a is /are by Maths experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- MAXIMA AND MINIMA Book:AAKASH SERIESChapter:MAXIMA AND MINIMA Exercise:ADDITIONAL PRACTICE EXERCISE (LEVEL - II (LECTURE SHEET )(ADVANCED)) (MATRIX MATCHING TYPE QUESTIONS)
Explore 2 Videos
- MAXIMA AND MINIMA Book:AAKASH SERIESChapter:MAXIMA AND MINIMA Exercise:ADDITIONAL PRACTICE EXERCISE (LEVEL - II (LECTURE SHEET )(ADVANCED)) (LINKED COMPREHENSION TYPE QUESTIONS)
Explore 6 Videos
- MAXIMA AND MINIMA Book:AAKASH SERIESChapter:MAXIMA AND MINIMA Exercise:ADDITIONAL PRACTICE EXERCISE (LEVEL - I (MAIN)) (STRAIGHT OBJECTIVE TYPE QUESTIONS)
Explore 50 Videos
- MAXIMA & MINIMABook:AAKASH SERIESChapter:MAXIMA & MINIMAExercise:EXERCISE-III
Explore 35 Videos
- MEAN VALUE THEOREMSBook:AAKASH SERIESChapter:MEAN VALUE THEOREMSExercise:PRACTICE SHEET (EXERCISE-I (LEVEL-II (MORE THAN ONE CORRECT ANSWER TYPE QUESTIONS ) )
Explore 2 Videos
Similar Questions
The function f(x)=√(ax3+bx2+cx+d) has its nonzero local minimum an d maximum values at x=-2 andx=2 , repectively . If a is a root of x2−x−x6=0 , then match the following
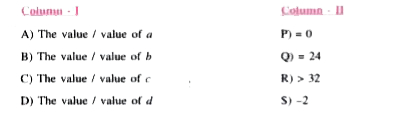
View SolutionSuppose you do not know the function f(x) , however some information about f(x) is listed below. Read the following carefully before attempting the questions
(i) f(x) is continuous and defined for all real numbers
(ii) f'(-5)=0 , f'(2) is not defined and f'(4)=0
(iii) (-5,12) is a point which lies on the graph of f(x)
(iv) f"(2) is undefined , but f"(x) is negative everywhere else.
(v) the signs of f(x) is given below

On the possible graph of y=f(x) we have
View SolutionThe minimum value of (A2+A+1)(B2+B+1)(C2+C+1)(D2+D+1)BACD , wher A,B,C,D are positive
View SolutionThe maximum slope of the curve y=−x3+3x2+9x−27 is
View SolutionGiven f(x) = 4- ((1)/(2) - x)^(2//3) , g(x) = {:{((tan[x])/(x),","x cancel(=)0),(1,","x=0):}" "h(x)={x}, k (x) = 5^(log_(2)(x+3))
Then in [0,1], Lagrange's mean value theorem is not applicable to (where [.] and {.} represents the greatest integer functions and fractions part functions, respectively )
View SolutionLet f(x) be an increasing function defined on (0,∞) . If f(2a2+a+1)>f(3a2−4a+1), then the possible integers in the range of a is/are 1 (b) 2 (c) 3 (d) 4
View SolutionLet f be the function f(x)=cosx−(1−x22). Then f(x) is an increasing function in (0,∞) f(x) is a decreasing function in (−∞,∞) f(x) is an increasing function in (−∞,∞) f(x) is a decreasing function in (−∞,0)
View SolutionLet f(x) be a increasing function defined on (0, ∞). If f(2a2+a+1)>f (3a2−4a+1). Find the range of a.
View SolutionLet f:(0,oo)rarr R be a (strictly) decreasing function.If f(2a^(2)+a+1)
View SolutionLet f:(−∞,2]→(−∞,4] be a function defined by f(x)=4x−x2. Then, f−1(x) is
View SolutionLet a function f:(2,∞)→[0,∞)defined as f(x)=|x−3||x−2|, then f is
View SolutionLet a function f:(0,∞)→[0,∞) be defined by f(x)=∣∣∣1−1x∣∣∣. Then f is
View SolutionLet f:[2,∞)→R be the function defined by f(x)=x2−4x+5, then the range of f is
View SolutionLet f(x) be an increasing function defined on (0,∞) . If f(2a2+a+1)>f(3a2−4a+1), then the possible integers in the range of a is/are (a)1 (b) 2 (c) 3 (d) 4
View SolutionLet f be the function f(x)=cosx−(1−x22). Then (a) f(x) is an increasing function in (0,∞) (b) f(x) is a decreasing function in (−∞,∞) (c) f(x) is an increasing function in (−∞,∞) (d) f(x) is a decreasing function in (−∞,0)
View Solution

