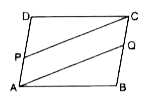
ABCD एक समान्तर चतुर्भुज है। भुजा AD पर बिंदु P इस प्रकार है कि AP=13AD तथा BC भुजा पर बिंदु Q इस प्रकार है कि CQ=13BC. सिद्ध कीजिए कि AQCP एक समान्तर चतुर्भुज है।
The correct Answer is:∴□APCQ एक समान्तर चतुर्भुज है
Step by step video, text & image solution for ABCD एक समान्तर चतुर्भुज है। भुजा AD पर बिंदु P इस प्रकार है कि AP = ( 1)/( 3) AD तथा BC भुजा पर बिंदु Q इस प्रकार है कि CQ = ( 1)/( 3) BC. सिद्ध कीजिए कि AQCP एक समान्तर चतुर्भुज है। by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Updated on:21/07/2023Topper's Solved these Questions
- समान्तर चतुर्भुज Book:S CHANDChapter:समान्तर चतुर्भुज Exercise:उदाहरण
Explore 18 Videos
- समान्तर चतुर्भुज Book:S CHANDChapter:समान्तर चतुर्भुज Exercise:प्रश्नावली 24.1
Explore 17 Videos
- समतल आकृतियों का क्षेत्रफल Book:S CHANDChapter:समतल आकृतियों का क्षेत्रफल Exercise:प्रश्नावली 28.8
Explore 8 Videos
- सम्बन्धित कोण Book:S CHANDChapter:सम्बन्धित कोण Exercise:प्रश्नावली 17.3
Explore 28 Videos
Similar Questions
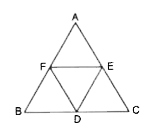
आकृति में एक समबाहु त्रिभुज ABC की भुजाओं BC,CA तथा AB के मध्य-बिंदु क्रमशः D,E तथा F हैं, तो सिद्ध करें कि ΔDEF भी एक समबाहु त्रिभुज हैं।
View Solutionसमान्तर चतुर्भुज ABCD में, यदि ∠A=110∘, तो ∠B,∠C,∠D का मान ज्ञात करें |
View Solutionएक चक्रीय चतुर्भुज की भुजाएँ क्रमशः 36 सेमी, 77 सेमी,75 सेमी और 40 सेमी हैं । इसका क्षेत्रफल ज्ञात करें।
View Solutionआकृति में, AB∣∣CD हो, तो x का मान ज्ञात कीजिए

View Solutionसिद्ध कीजिये की बिंदु (1,−2),(3,6),(5,10) और (3,2) एक समांतर चतुर्भुज के शीर्ष है ।
View Solutionसिद्ध कीजिए कि बिंदु (1,−6),(5,2),(7,0) तथा (−1,−4)एक चक्रीय चतर्भुज के शीर्ष है ।
View Solutionएक ही आधार BC पर तीन समद्विबाहु त्रिभुज △PBC ,△QBC और △RBC स्तिथ है। सिद्ध कीजिए कि P ,Q और R समरेख है।
View Solutionयदि ¯a,¯b दो सदिश इस प्रकार है कि ∣∣¯a+¯b∣∣=|¯a|, तो सिद्ध कीजिए कि 2¯a+¯b सदिश ¯b पर लम्ब है |
View Solutionयदि दो सदिश ¯a और ¯b इस प्रकार हैं कि ∣∣¯a+¯b∣∣=∣∣¯b∣∣, तब सिद्ध कीजिए कि ¯a+2¯b, सदिश ¯a पर लम्ब है |
View Solutionमाना कि ABCD एक समान्तर चतुर्भुज इस प्रकार हो कि ¯¯¯¯¯¯AB=¯q तथा ¯¯¯¯¯¯AD=¯p और ∠BAD एक न्यून कोण है | यदि सदिश ¯r, शीर्ष B से भुजा AD पर खींचे गए लम्ब के सम्पाती हो तो ¯r =
View Solutionसम्मिश्र संख्याओं z कि संख्या जो इस प्रकार |z−1|=|z+1|=|z−i|है, है :
View Solutionदो स्थिर बिंदुओं A और B के निर्देशांक क्रमश :(5,3) और (3,−2) है । बिंदु P इस प्रकार गमन करता है कि त्रिभुज PAB का क्षेत्रफल 9 वर्ग क्षेत्रफल वर्ग मात्रक रहता है । बिंदु P का बिन्दुपथ ज्ञात कीजिए ।
View Solutionएक बिंदु इस प्रकार गमन करता है कि उसकी बिंदु (3,4) से दुरी बिंदु (−3,−4) से उसकी दूरी की तिगुनी रहती है । उसका बिन्दुपथ ज्ञात कीजिए ।
View Solutionकिसी त्रिभुज ABC में A(a,0)औरB(−a,0) बिंदु है । शीर्ष C इस प्रकार गमन करता है कि tanA+tanB=2 . बिंदु C का बिन्दुपथ ज्ञात कीजिए ।
View Solutionयदि परिमेय संख्याओं के समुच्चय Q पर संक्रिया (∗) इस प्रकार परिभाषित है कि a∗b=2a+3b . दिखाइए कि (∗) समुच्चय Q पर एक द्विआधारी संक्रिया है।
View Solutionयदि f:R→R इस प्रकार है कि f(x) = |x|, तो सिद्ध कीजिए कि fof = f .
View Solution

