A 12.5 eV electron beam is used to bombard gaseous hydrogen at room temperature. What series of wavelengths will be emitted?Solution in Gujrati

Video Solution
Doubtnut Promotions Banner
Text Solution
Verified by Experts

Ground state energy of hydrogen gas at room temperature = - 13.6 eV.
When the energy beam used to bombard gaseous hydrogen then its energy becomes = - 13.6 + 12.5 eV = -1.1 eV.
Now energy in nth orbit
En=−13.6n2eV
∴−1.1eV=13.6n2eV
∴n2=13.61.1=12.36
∴n=3.51
but possibel orbits n=3
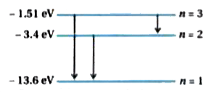
ocr_image
∴ Spectral line of emiision spectra
=n(n−1)2
=3(−1)2
=3
Hence in transition from n = 3 to n = 1 an n = 2 to n = 1 two lines of Lyman series and i transition n = 3 to n = 2, one line of Balme series are obtained.
⇒ In transition from n = 3 to n = 1 th wavelength of β-line emitted in Lyman series.
λ31=hcE1−E3=6.62×10−34×3×108(−13.6−(−1.51))
∴λ31=19.875×10−2612.09×1.6×10−19
=1.0274×10−7m
≈103×10−9m=103m
In transition from n = 2 to n = 1, the wavelength of c-line emitted in Lyman series,
λ21=hcE1−E2=6.625×10−34×3×108[−13.6−(3.4)]eV
=19.875×10−2610.2×1.6×10−19
=1.2178×10−7m
≈122×10−9m=122mm
⇒ In transition from n = 3 to n = 2. wavelength of a-line emitted in Balmer series,
λ32=hcE2−E3=6.625×10−34×3×108[−3.4−(−1.51)]eV
∴λ32=19.875×10−261.89×1.6×10−19
6.5724×10−7m
=657×10−9m
657nm

Updated on:21/07/2023
|
Class 12PHYSICSATOMS

Topper's Solved these Questions

Similar Questions