माना बिन्दुओ A, B, C के निर्देशांक (acosθ1,asinθi)i=1,2,3द्वारा निरूपित किये जाते है तथा cs(θ1−θ2)+cos(θ2−θ3)+cos(θ3−θ1)=−32 है
1 : ΔABC का लम्बकेन्द्र (0, 0) है।
2 : ΔABC एक समबाहु त्रिभुज है।
कथन- 1 सत्य है , कथन - 2 सत्य यही, कथन-2 कथन-1 का सही स्प्ष्टीकरण है।
कथन- 1 सत्य है, कथन-2 सत्य है, कथन-2 कथन-1 का सही स्पष्टीकरण ugh है।
कथन-1 सत्य है, कथन-2 असत्य है।
कथन-1 असत्य है, कथन-2 सत्य है।
The correct Answer is:A
Step by step video, text & image solution for माना बिन्दुओ A, B, C के निर्देशांक (a cos theta_(1), a sin theta _(i)) i = 1, 2, 3 द्वारा निरूपित किये जाते है तथा cs (theta_(1) - theta_(2)) + cos (theta_(2) - theta_(3)) + cos (theta_(3) - theta_(1)) = - (3)/(2) है 1 : Delta ABC का लम्बकेन्द्र (0, 0) है। 2 : Delta ABC एक समबाहु त्रिभुज है। by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- सरल रेखा Book:BANSAL HINDIChapter:सरल रेखा Exercise:Exercise - (Special Dpp - 7 ) Paragraph
Explore 2 Videos
- सरल रेखा Book:BANSAL HINDIChapter:सरल रेखा Exercise:Exercise - (Special Dpp - 8 )
Explore 11 Videos
- सरल रेखा Book:BANSAL HINDIChapter:सरल रेखा Exercise:Exercise - (Special Dpp - 6 ) Paragraph
Explore 11 Videos
- सदिश एवं त्रिविम निर्देशांक ज्यामितीय (VECTOR & 3-D)Book:BANSAL HINDIChapter:सदिश एवं त्रिविम निर्देशांक ज्यामितीय (VECTOR & 3-D)Exercise:EXERCISE-5 (RANK BOOSTER)
Explore 13 Videos
Similar Questions
एक समबाहु त्रिभुज ABC का केन्द्रक मूल बिन्दु (0,0) पर है तथा इसका आधार BC रेखा x + y = 1 के अनुदिश है, तो
समबाहु ΔABC का क्षेत्रफल है
View Solutionरेखाओ |x| + |y| = 2 द्वारा निर्मित चतर्भुज का क्षेत्रफल है
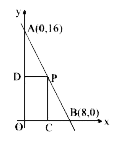
View Solutionचित्र में दिखाये अनुसार, बिन्दुओ A(0, 16) तथा B(8,0) से गुजरने वाली एक रेखा खींची जाती है। A एवं B से गुजरने वाली रेखा पर प्रथम चतुर्थांश में एक बिन्दु P लिया जाता है। x एवं y-अक्ष पर क्रमशः बिन्दु c एवं D इस प्रकार लिये जाते है कि PDOC एक आयत है।
रेखा AB की बिन्दु (2, 2) से लम्बवत् दुरी है
View Solutionकिसी चतुष्फलक के शीर्ष A,B,C की स्थिति सदिश क्रमशः (1,1,1),(1,0,0) तथा (3,0,0) है। यदि शीर्ष D से विपरीत तल ABC पर लंब डाला जाता है तथा यह त्रिभुज ABC के शीर्ष A से जाने वाली माध्यिका पर बिंदु E पर मिलता है। यदि AD की लम्बाई 4 तथा चतुष्फलक का आयतन 2√23 है। तो E की स्थिति ज्ञात कीजिए।
View SolutionIf sinθ1+sinθ2+sinθ3=3, then cosθ1+cosθ2+cosθ3 is equal to
(a) 3
(b) 2
(c) 1
(d) 0
View SolutionIf ABC having vertices A(acosθ1,asinθ1),B(acosθ2asinθ2),andC(acosθ3,asinθ3) is equilateral, then prove that cosθ1+cosθ2+cosθ3=sinθ1+sinθ2+sinθ3=0.
View SolutionIf (acosθ1,asinθ1),(acosθ2,asinθ2) and (acosθ3,asinθ3) represent the vertices of an equilateral triangle inscribed in a circle, then (a) cosθ1+cosθ2+cosθ3=0 (b) sinθ1+sinθ2+sinθ3=0 (c) tanθ1+tanθ2+tanθ3=0 (d) cotθ1+cotθ2+cotθ3=0
View SolutionIF A(cosθ1,sinθ1),B(cosθ2,sinθ2)&C(cosθ3,sinθ3), then Orthocenter of ΔABC is
View SolutionIf sinθ1+sinθ2+sinθ3, then find the value of cosθ1+cosθ2+cosθ3.
View SolutionIf (cos theta_(1),sin theta_(1)),B(cos theta_(2),sin theta_(2)) and C(cos theta_(3),sin theta_(3)) then orthocenter of Delta ABC is
View SolutionIf (acosθ1,asinθ1),(acosθ2,asinθ2),(acosθ3,asinθ3) represents the vertices of an equilateral triangle inscribed in x2+y2=a2, then
View SolutionIf cosθ1cosθ2+sinθ1sinθ2=cosθ0cosθ2+sinθ0sinθ2=1, where θ1 and θ0 do not differ by can even multiple of π, prove that
cosθ1⋅cosθ0cos2θ2+sinθ1⋅sinθ0sin2θ2=−1
View Solutionयदि sinθ1+sinθ2+sinθ3+sinθ4=4, है cosθ1+cosθ2+cosθ3+cosθ4 का मान है
View SolutionIf θ1,θ2,θ3....,θn are in A.P. then sinθ1+sinθ2+...+sinθncosθ1+cosθ2+...+cosθn=
View SolutionIf cos(θ1−θ2)cos(θ1+θ2)+cos(θ3+θ4)cos(θ3−θ4)=0 then
tanθ1.tanθ2.tanθ3.tanθ4=
View Solution

