एक ΔABC के शीर्षलम्ब AD, BE तथा CF बराबर है सिद्ध करे कि ΔABC समबाहु त्रिभुज है।
The correct Answer is:ΔABC एक समबाहु त्रिभुज है
Step by step video, text & image solution for एक DeltaABC के शीर्षलम्ब AD, BE तथा CF बराबर है सिद्ध करे कि DeltaABC समबाहु त्रिभुज है। by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Topper's Solved these Questions
- BOOK - S CHANDCHAPTER - त्रिभुजों की सर्वांगसमता EXERCISE - प्रश्नावली 20.114videos
त्रिभुजों की सर्वांगसमता
- BOOK - S CHANDCHAPTER - त्रिभुजों की सर्वांगसमता EXERCISE - प्रश्नावली 20.28videos
त्रिभुजों की सर्वांगसमता
- BOOK - S CHANDCHAPTER - त्रिभुजों की संगामी रेखाएँEXERCISE - प्रश्नावली 23.1 (रिक्त स्थानों की पूर्ति करे) :6videos
त्रिभुजों की संगामी रेखाएँ
- BOOK - S CHANDCHAPTER - दो चरों वाले रैखिक समीकरण EXERCISE - प्रश्नावली 7.228videos
दो चरों वाले रैखिक समीकरण
Similar Questions
यदि निम्नलिखित में से कोई भी सत्य है तो सिद्ध करें कि ΔABC एक समद्विबाहु त्रिभुज है।
∠BAC का समद्विभाजक BC पर लम्ब है07:55View SolutionΔABC में, ∠A=90∘,AB=AC तो ∠B और ∠C ज्ञात करें
02:16View Solutionएक त्रिभुज की भुजाओ के लंबार्धक…………...बिन्दु से होकर जाते है।
07:05View Solutionकोटि 0 वाले बिन्दु कहाँ पर स्थित होते है ?
07:31View Solutionसिद्ध कीजिये की बिंदु (a,a),(-a,-a),(-a√3,a√3) एक समबाहु त्रिभुज के निर्देशांक है
07:02View Solutionयदि ΔABCके शीर्षलम्ब AD,BE तथा CF समान हैं, तो सिध्द करो कि ΔABCएक समबाहु त्रिभुज है |
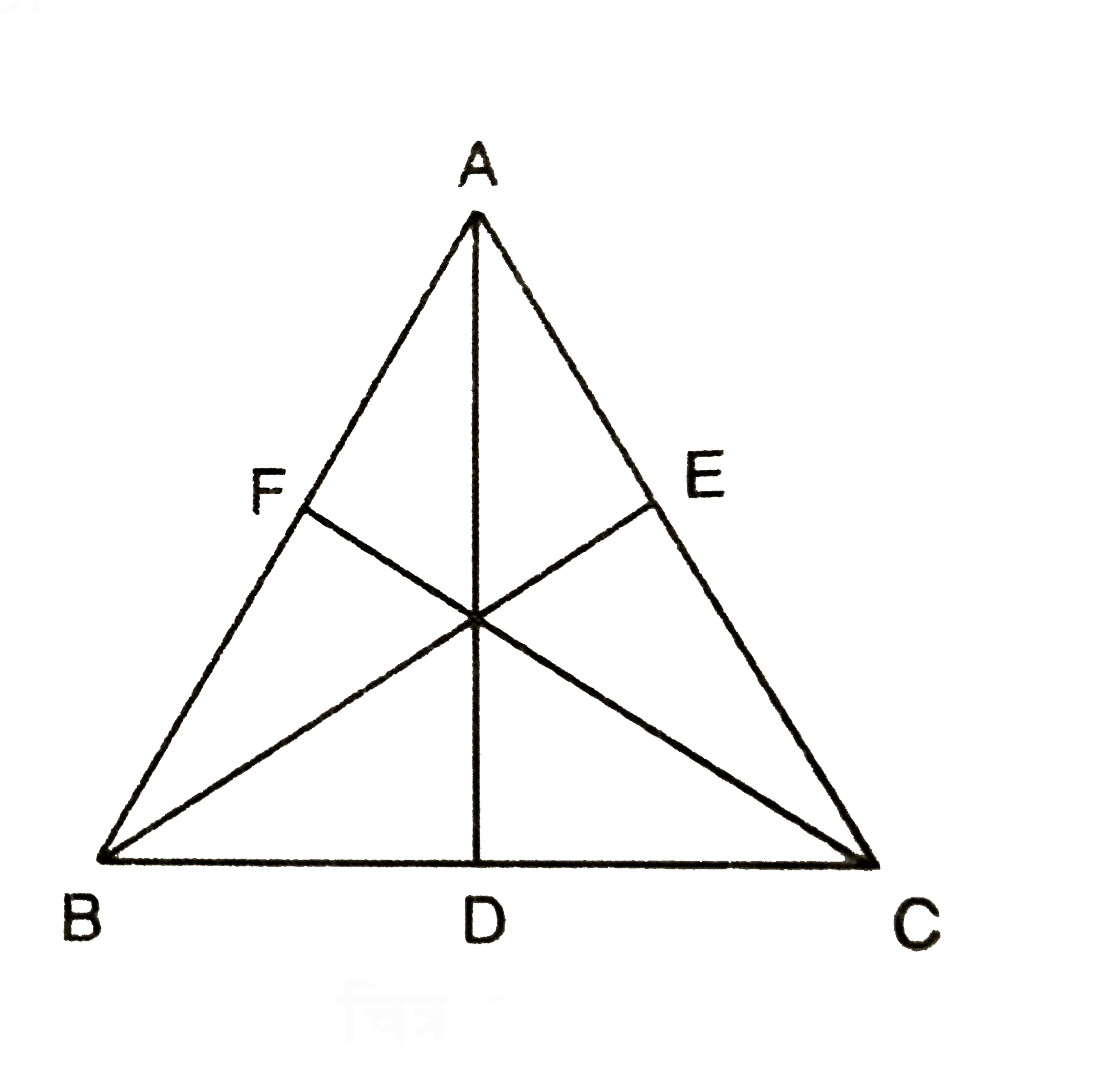 04:32View Solution
04:32View Solutionकिसी समबाहु त्रिभुज के आधार का समीकरण x+y=2 है तथा सामने के शीर्ष के निर्देशांक (2,1) है , त्रिभुज की शेष भुजाओ के समीकरण ज्ञात कीजिए ।
05:40View Solutionकिसी त्रिभुज कि भुजाओ के मध्य बिन्दुओ के निर्देशांक क्रमशः (2,1),(−5,7) तथा (−5,5) है त्रिभुज कि भुजाओ के समीकरण ज्ञात कीजिए ।
02:46View Solutionसिद्ध कीजिए कि बिंदु (1,−6),(5,2),(7,0) तथा (−1,−4)एक चक्रीय चतर्भुज के शीर्ष है ।
04:17View SolutionIf AD , BE and CF are medians of ΔABC, then ¯¯¯¯¯¯AD+¯¯¯¯¯¯BE+¯¯¯¯¯¯CF =
06:21View Solutionसिद्ध कीजिए कि ΔABC एक समद्विबाहु त्रिभुज है यदि
∣∣ ∣ ∣∣1111+cosA1+cosB1+cosCcos2A+cosAcos2B+cosBcos2C+cosC∣∣ ∣ ∣∣=003:33View Solutionमाना कि N में एक द्वि - आधारी संकिया ∗, a∗b=a तथा b के LCM द्वारा परिभाषित है , a,b∈N तब सिद्ध कीजिए कि :(20∗16)∗8=20∗(16∗8)
04:32View Solutionसदिश विधि से सिद्ध करें कि यदि किसी त्रिभुज दो मध्यिकाएँ बराबर हों, तो त्रिभुज समद्विबाहु होता है |
04:10View Solutionकिसी त्रिभुज ABC की माध्यिकाएँ AD, BE, CF बिन्दु G पर मिलती हैं | दर्शाइए कि :
ΔAGB=ΔBGC=ΔCGA=13ΔABC.05:27View Solutionसिद्ध कीजिए कि सम्मिश्र संख्याओं 0, 2i और √3+i को निरूपित करने वाले बिंदु समबाहु त्रिभुज के शीर्ष है।
43:46View Solution
